橢圓曲線密碼系統(ECC)與其他公鑰加密系統相比,因其密鑰長度短、安全強度高等諸多優點,被公認為最有前途的公鑰密碼體系,受到人們的普遍關注和研究[1-4]。
在國內外有關ECC的研究方面,主要集中在 ECC的時間復雜度和空間復雜度上[2-4]。參考文獻[2]研究模逆和標乘的快速算法,參考文獻[3]針對KP算法將改進的Booth算法嵌入傳統算法,極大地降低了迭代次數和有限域運算量。參考文獻[4]將所有的模運算全轉化為模乘運算和模加運算,并改進了LSD乘法器,利用該單元進行模運算,從而其硬件實現了具有面積小、速度快等優點。
目前國內的密碼技術還是落后于國外,特別是在生活應用中,國內的企業基本上是引用國外的密碼技術進行二次開發。如果要將實現的橢圓曲線密碼系統應用到實際中,則需要通過系統集成芯片設計(SOC),將FPGA上實現的橢圓曲線密碼系統集成實用性的加密芯片。一旦設計過程中所需的資源和條件不夠完善,將導致加密芯片的制作難以實現。為此,本文借助Xilinx公司提供的強大的系統級硬件仿真工具System Generator[5],研究并設計ECC加解密系統。
1 橢圓曲線密碼體制
由于最終是要在硬件上實現橢圓曲線密碼體制[6],所以本文選擇的有限域是特征為2的GF(2n),選擇的橢圓曲線方程如式(1)所示。


可見橢圓曲線密碼體制涉及到GF(2n)上的模加運算、模乘運算、求逆運算,還有橢圓曲線的KP點乘運算,下面對幾個主要算法進行分析。
1.1 GF(2n)域上的模乘運算
模乘模塊是整個設計中最關鍵的模塊,模乘的過程包括多項式相乘和取模兩個過程。傳統的乘法器是將兩個m位操作數相乘,然后對其進行f(x)求模。這樣的缺點就是需要一個2m位的寄存器來存儲中間結果,勢必會浪費資源。本文采用全串行移位相加法來實現模乘運算[6]。該算法只有簡單的移位和“異或”運算,但是需要大量的移位運算,如果A、B具有m位,則需要進行m-1次移位運算,這是比較耗時的。
但是本文使用的FPGA工作在61.44 MHz時鐘下,m一般取值在200左右,因此全串行移位相加法大概需要的是ns級的時間,而且全串行移位算法也是最節省資源的算法。通過Modelsim仿真該模塊,得到圖1所示結果。其中, clk是系統時鐘61.44 MHz;reset是系統復位信號;en是使能端口;din是乘數輸入端口,低位在前;dout是輸出結果;rdy是輸出結果有效指示。

1.2 GF(2n)域上的模逆運算
對于GF(2n)域上的模逆運算,當今最有效的算法就是擴展歐幾里德算法和基于費馬定理的模逆算法。擴展歐幾里德算法用時會比基于費馬定理的模逆算法用時短很多,但是相應地是以犧牲硬件資源為代價,在后面的點乘算法和最后的橢圓曲線密碼體制的實現耗用資源很大。
擴展歐幾里德算法還要去另外設計一個多項式模塊,而基于費馬定理的模逆算法只需要反復調用先前做好的模乘模塊就行,再加上本文用的FPGA時鐘頻率本身就高,因此本文選擇費馬定理來做模逆算法。通過Modelsim仿真該模塊,得到圖2所示結果。其中,clk是系統時鐘61.44 MHz;reset是系統復位信號;en是模逆使能;din是輸入數據;a_inv是輸出結果;rdy是輸出結果有效指示。

選取參數:
K=157E51751D89C66CBDF44596BF7F653876A18C4B12
40B85A;
x=36B3DAF8A23206F9C4F299D7B21A9C369137F2C84
AE1AA0D;
y=7658E73433B3F95E332932E70EA245CA2418EA0EF9
8018FB;
b=2E45EF571F00786F67B0081B9495A3D95462F5DE0A
A185EC;
f=800000000000000000000000000000000000000000000
201。
仿真結果:
Cx=34EEC5768673E71B8CDC139FB8EB4ACD9989FAA
E1EC9EF1D;
Cy=779097F490A2DA7A6B09A9518733B4817D5C21947
547D2A1。
2 System Generator搭建ECC加密系統
System Generator是業內領先的高級系統級FPGA開發工具。其作用是借助FPGA設計高性能DSP系統并和Simulink實現無縫鏈接,快速建模并自動生成代碼[5]。System Generator最大的特點就是可利用Simulink建模和仿真環境來實現FPGA設計,無需了解和使用RTL級硬件語言,讓DSP設計者能夠發揮基于FPGA的DSP的最大性能和靈活性,并縮短整個設計周期。
前文用FPGA實現了ECC的各個關鍵模塊,下面用先前生成的各個模塊代碼通過System Generator的黑盒子生成各自相應的模塊。再將這些模塊搭建成完整的ECC模塊,以便在Matlab工作空間中輸入相應的參數、明文和相應的使能端口就可以實現加密;輸入相應的參數、密文和相應的使能端口就可以實現解密。但是本文所涉及的參數較大,輸入的過程很耗費時間,因此本文將參數都固定在一個ROM中間,只要控制相應的使能信號,就可以達到一個加解密的模擬過程。
2.1數據輸入模塊的搭建
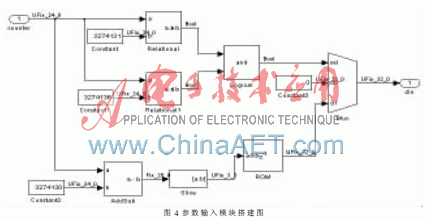
本文中的端口有使能端口和參數端口,其中,使能端口是1 bit的,就可以用計數器來實現。對于191個bit位的參數,可先將其分解成6組的32 bit系數, 存在如圖4所示的ROM中,只要改變ROM中的值就可以控制輸入參數的值,改變3個常數模塊就可以控制參數輸入的時刻。
2.2 ECC系統的搭建與仿真結果
利用代碼生成的KP模塊、求逆模塊和乘法模塊搭建成ECC加解密系統。由于ECC加解密系統的各個子模塊有很多的反饋端口,搭建起來的圖顯得比較亂,因此可以在ECC系統中的m文件添加 this block.addFile()。把各個子模塊添加到ECC頂層模塊中,這樣就相當于把各個子模塊集成在統一的黑盒子中。
設置運行時間為4 000 000個時鐘周期,將加解密指示信號設置為加密,點擊運行,進行加密仿真,在工作區間可以看到,明文輸入和對應的密文輸出。例如,當輸入的明文為“4129534493046158328227537522838960054530294419451055575666”時,輸出的密文為“3625519732263338515328819742424233936313311718087”。
設置運行時間為4 000 000個時鐘周期,將加解密指示信號設置為解密,點擊運行,進行解密仿真,在工作區間可以看到密文輸入和對應的的明文輸出。例如,當輸入的密文為“362551973226333851532881974242423393631
3311718087”, 則輸出的明文為“4129534493046158328227537522838960054530294419451055575666”。
ECC模塊加解密運算輸出有效數據的時鐘周期是第3274550,使能信號則是在第11個時鐘周期輸入,因此整個運算過程中數據的輸入輸出所耗費的時間是3274550-11=3 274 539個時鐘周期,所以對于采用時鐘頻率為61.44 MHz的FPGA來說,只要用3 274 539/61.44 ?滋s就可以完成一次加密算法,或者一次解密算法。總共用的時間為3274539/61.44 ns=53.3 ms,而若單單只用Matlab仿真運行,大概需要時間為20 min。因此采用硬件實現橢圓曲線密碼系統的優越性不言而喻。
參考文獻
[1] HANKERSON D,MENEZES A, VANSTONE S. Guide to elliptic curve cryptography[M]. Springer Verlag New York Inc,2004:25-147.
[2] MA S W, HAO Y L, PAN Z Q. Fast implementation for modular inversion an d scalar multiplication in the elliptic curve cryptography[C].IITA ’08,Beijing,China,2008:488-492.
[3] 龔書,劉文江,戎蒙恬。一種橢圓曲線密碼加密算法及實現[J]。高技術通訊,2004(3):25-28.
[4] 唐薛峰,沈海斌,嚴曉浪.GF(2^m)上橢圓密碼體制的硬件實現[J]。計算機工程與應用,2004,40(11):96-98.
[5] 田耕,徐文波,胡彬.Xilinx ISE Design Suite 10.x FPGA開發指南[M]。北京:人民郵電出版社,2008.
[6] 祝躍飛,張亞娟。橢圓曲線公鑰密碼導引[M]。 北京:科學出版社,2006.
編輯:jq
-
dsp
+關注
關注
553文章
7998瀏覽量
348925 -
FPGA
+關注
關注
1629文章
21736瀏覽量
603387 -
soc
+關注
關注
38文章
4165瀏覽量
218260 -
LSD-
+關注
關注
0文章
2瀏覽量
9014
發布評論請先 登錄
相關推薦
4G模組Air780E的LuatOS開發:關于通用加解密函數(crypto)教程!

SoC的數字簽名加解密過程
國內大型汽車集團3套SAP ECC系統選擇性拆分&升級成功上線
DDR Inline ECC在Jacinto7 SoC中的應用

PSoC5LP:ECC總是返回失敗的原因?
CYT4BF的監管區 (SFlash) 是否支持 ECC?
鴻蒙OS開發問題:(ArkTS)【 RSA加解密,解決中文亂碼等現象】
芯來科技正式發布基于RISC-V處理器的HSM子系統解決方案
設備監察系統(Facilities Monitoring System)簡介
Pflash和Dflash都有閃存ECC保護,ECC內存在哪里?
基于FPGA的可編程AES加解密IP





 簡述System Generator的ECC加解密系統的設計
簡述System Generator的ECC加解密系統的設計













評論