下面我們將鏡頭切到袁記菜館。
小二:掌柜的,最近大家都在忙著種樹,說是要保護環境。
老板娘:樹 ? 咱們店有呀,前幾年種的那棵葡萄樹,不是都結果子了嗎?就數你吃的最多。
小兒:這...
大家應該猜到,咱們今天要嘮啥了。
之前給大家介紹了鏈表,棧,哈希表 等數據結構
今天咱們來看一種新的數據結構,樹。
PS:本篇文章內容較基礎,對于沒有學過數據結構的同學會有一些幫助,如果你已經學過的話,也可以復習一下,查缺補漏,后面會繼續更新這個系列。
樹
我們先來看下百度百科對樹的定義
樹是 n (n 》= 0) 個節點的有限集。n = 0 時 我們稱之為空樹, 空樹是樹的特例。
在任意一棵非空樹中:
有且僅有一個特定的節點稱為根(Root)的節點
當 n 》 1 時,其余節點可分為 m (m 》 0)個互不相交的有限集 T1、T2、....Tm,其中每一個集合本身又是一棵樹,并且稱為根的子樹。
我們一起來拆解一下上面的兩句話,到底什么是子樹呢?見下圖
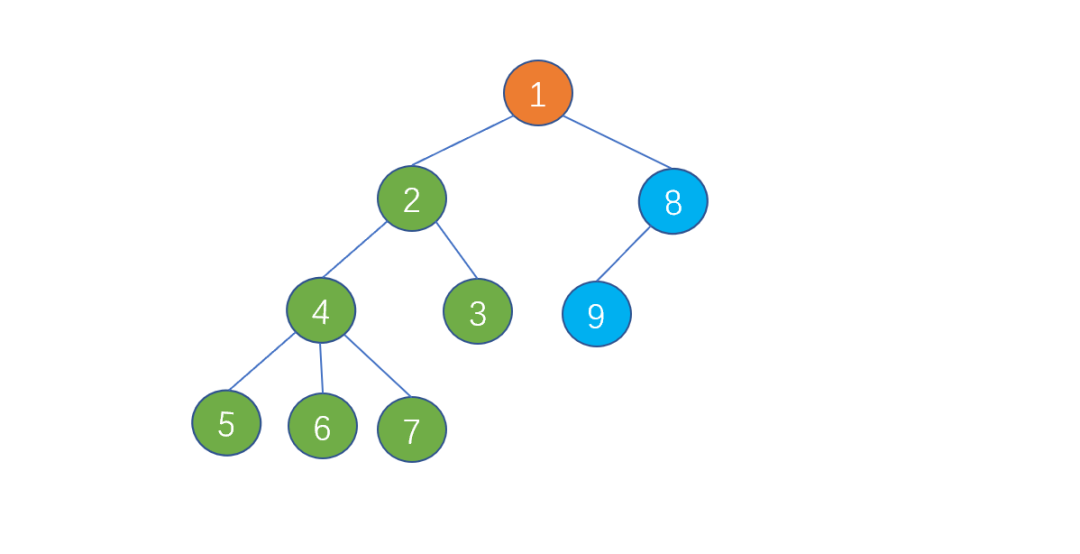
樹
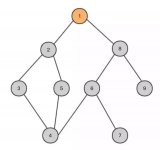
例如在上面的圖中
有且僅有一個特定的節點稱為根節點,也就是上圖中的橙色節點。
當節點數目大于 1 時,除根節點以外的節點,可分為 m 個互不相交的有限集 T1,T2.。..。...Tm。
例如上圖中,我們將根節點以外的節點,分為了 T1 (2,3,4,5,6,7),T2(8,9)兩個有限集。
那么 T1 (綠色節點)和 T2(藍色節點)就是根節點(橙色節點)的子樹。
我們拆解之后發現,我們上圖中的例子符合樹的要求,另外不知道大家有沒有注意到這個地方。
除根節點以外的節點,可分為 m 個互不相交的有限集。
那么這個互不相交又是什么含義呢?見下圖。
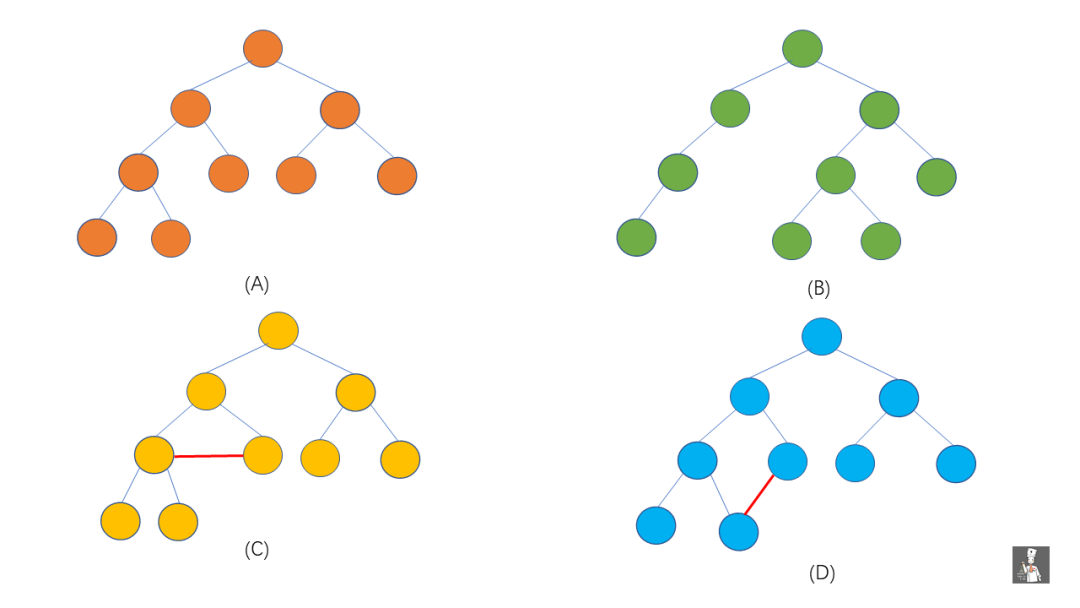
我們將 (A) , (B) , (C) , (D) 代入上方定義中發現,(A) , (B) 符合樹的定義,(C), (D) 不符合,這是因為 (C) , (D) 它們都有相交的子樹。
好啦,到這里我們知道如何辨別樹啦,下面我們通過下面兩張圖再來深入了解一下樹。
主要從節點類型,節點間的關系下手。
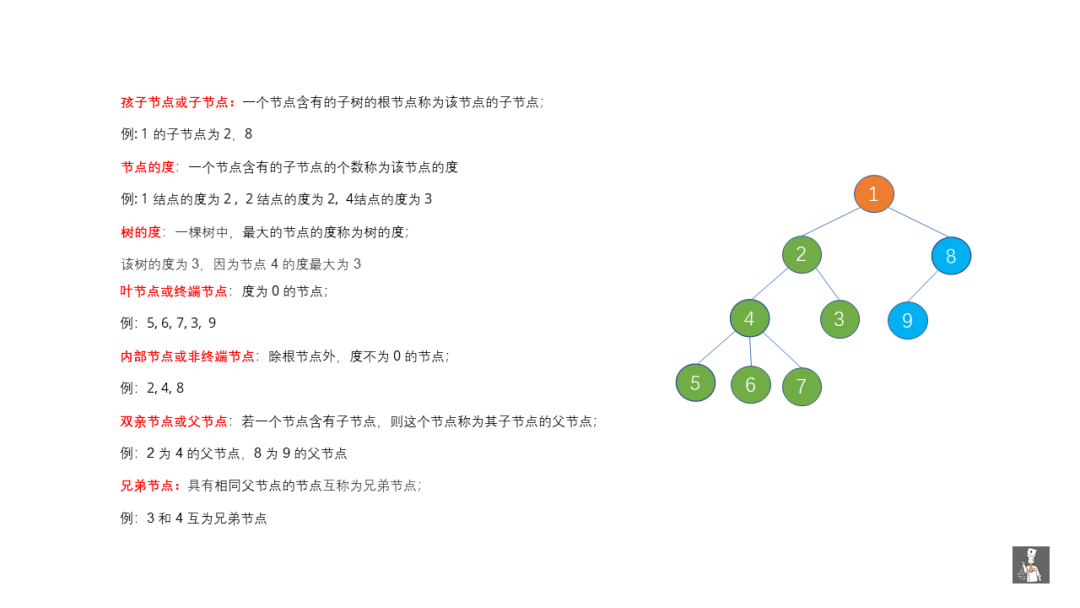
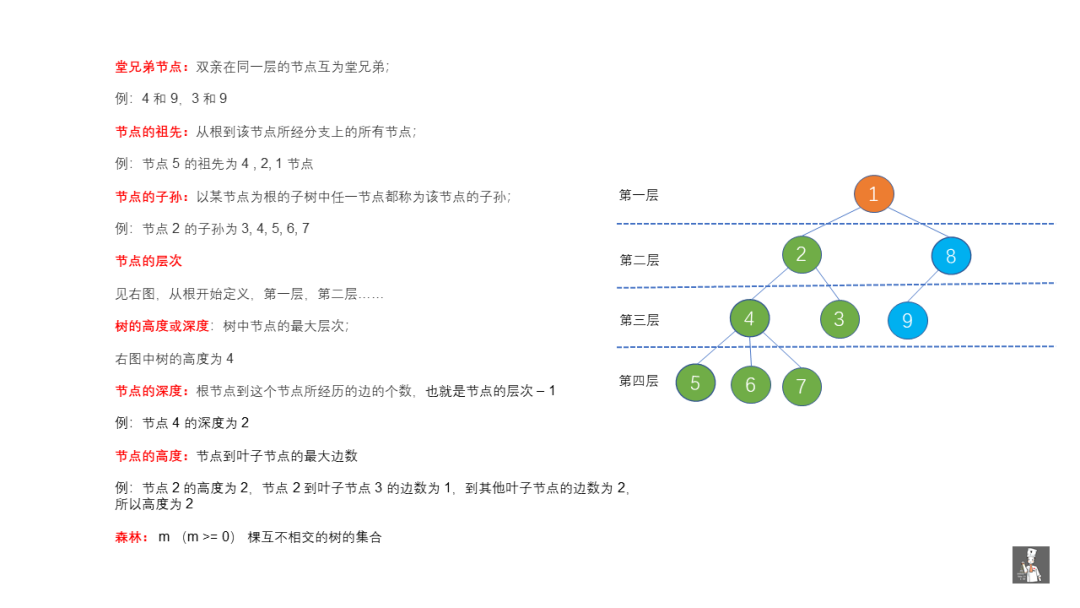
這里節點的高度和深度可能容易記混,我們代入到現實即可。
我們求物體深度時,從上往下測量,求高度時,從下往上測量,節點的高度和深度也是如此。
二叉樹
我們刷題時遇到的就是二叉樹啦,下面我們一起來了解一下二叉樹
二叉樹前提是一棵樹,也就是需要滿足我們樹的定義的同時,還需要滿足以下要求
每個節點最多有兩個子節點,分別是左子節點和右子節點。
注意我們這里提到的是最多,所以二叉樹并不是必須要求每個節點都有兩個子節點,也可以有的僅有一個左子節點,有的節點僅有一個右子節點。
下面我們來總結一下二叉樹的特點
每個節點最多有兩棵子樹,也就是說二叉樹中不存在度大于 2 的節點,節點的度可以為 0,1,2。
左子樹和右子樹是有順序的,有左右之分。
假如只有一棵子樹 ,也要區分它是左子樹還是右子樹
好啦,我們已經了解了二叉樹的特點,那我們分析一下,下圖中的樹是否滿足二叉樹定義,共有幾種二叉樹。
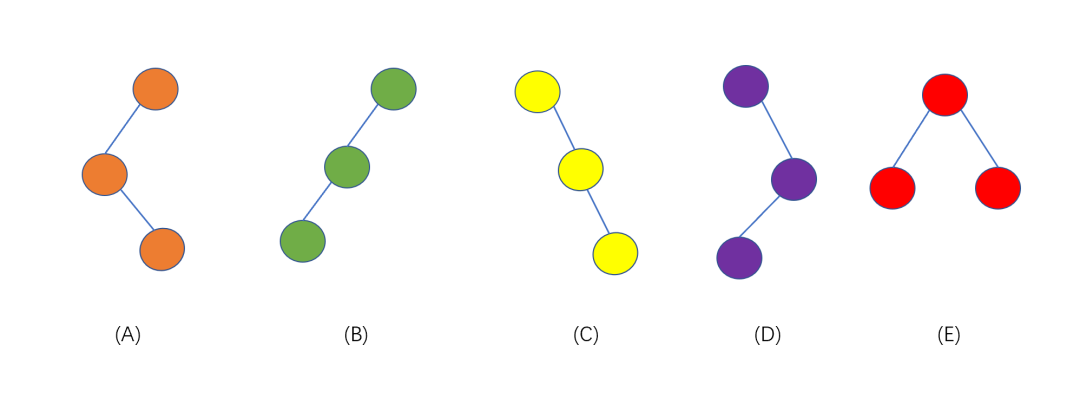
上圖共為 5 種不同的二叉樹,在二叉樹的定義中提到,二叉樹的左子樹和右子樹是有順序的,所以 B,C 是兩個不同的二叉樹,故上圖為 5 種不同的二叉樹。
特殊的二叉樹
下面我們來說幾種比較特殊的二叉樹,可以幫助我們刷題時,考慮到特殊情況。
滿二叉樹
滿二叉樹:在一棵二叉樹中,所有分支節點都存在左子樹和右子樹,并且所有的葉子都在同一層,這種樹我們稱之為滿二叉樹。見下圖
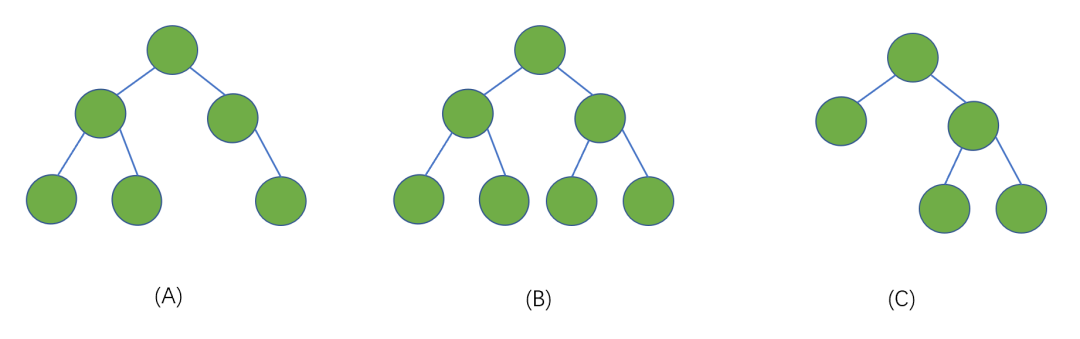
我們發現只有 (B) 符合滿二叉樹的定義,我們發現其實滿二叉樹也為完全二叉樹的一種。
完全二叉樹
完全二叉樹:葉子結點只能出現在最下層和次下層,且最下層的葉子結點集中在樹的左部。
哦!我們可以這樣理解,除了最后一層,其他層的節點個數都是滿的,而且最后一層的葉子節點必須靠左。
下面我們來看一下這幾個例子
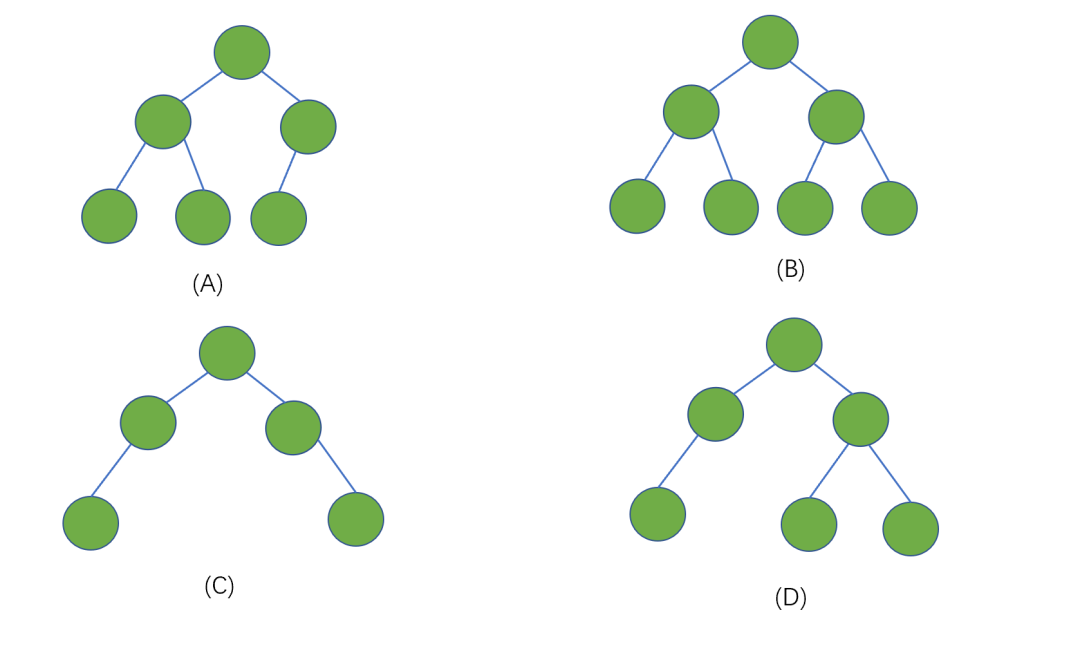
上面的幾個例子中,(A)(B)為完全二叉樹,(C)(D)不是完全二叉樹
斜二叉樹
這個就很好理解啦,斜二叉樹也就是斜的二叉樹,所有的節點只有左子樹的稱為左斜樹,所有節點只有右子樹的二叉樹稱為右斜樹。
諾,下面這倆就是。
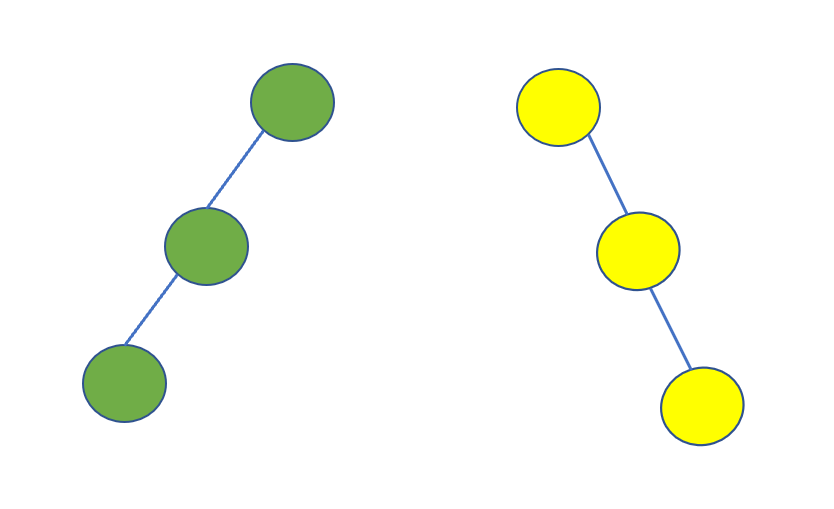
另外還有 一些二叉樹的性質, 比如第 i 層至多有多少節點,通過葉子節點求度為 2 的節點, 通過節點樹求二叉樹的深度等, 這些是考研常考的知識, 就不在這里進行贅述,需要的同學可以看一下王道或者天勤的數據結構, 上面描述的很具體, 并附有證明過程。
好啦,我們已經了解了二叉樹,那么二叉樹如何存儲呢?
如何存儲二叉樹
二叉樹多采用兩種方法進行存儲,基于數組的順序存儲法和基于指針的二叉鏈式存儲法
我們在之前說過的堆排序中,其中對堆的存儲采用的則是順序存儲法,具體細節可以看這篇文章
一個破堆排我搞了 4 個動畫?
這里我們再來回顧一下如何用數組存儲完全二叉樹。
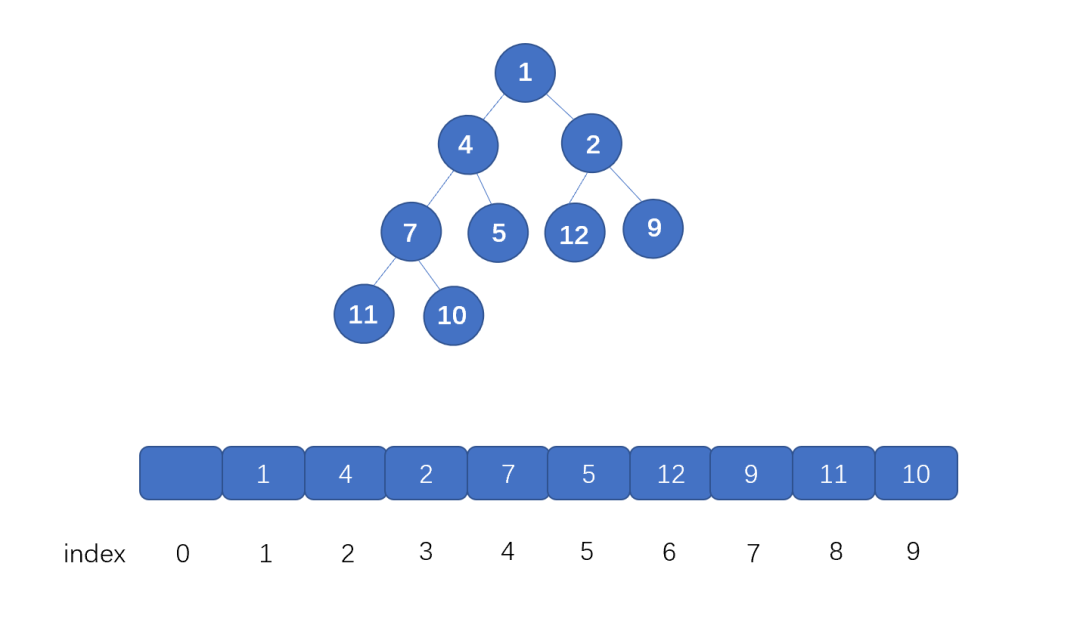
我們首先看根節點,也就是值為 1 的節點,它在數組中的下標為 1 ,它的左子節點,也就是值為 4 的節點,此時索引為 2,右子節點也就是值為 2 的節點,它的索引為 3。
我們發現其中的關系了嗎?
數組中,某節點(非葉子節點)的下標為 i , 那么其左子節點下標為 2*i(這里可以直接通過相乘得到左孩子, 也就是為什么空出第一個位置, 如果從 0 開始存,則需要 2i+1 才行), 右子節點為 2i+1,其父節點為 i/2 。既然我們完全可以根據索引找到某節點的 左子節點 和右子節點,那么我們用數組存儲是完全沒有問題的。
但是,我們再考慮一下這種情景,如果我們用數組存儲斜樹時會出現什么情況?
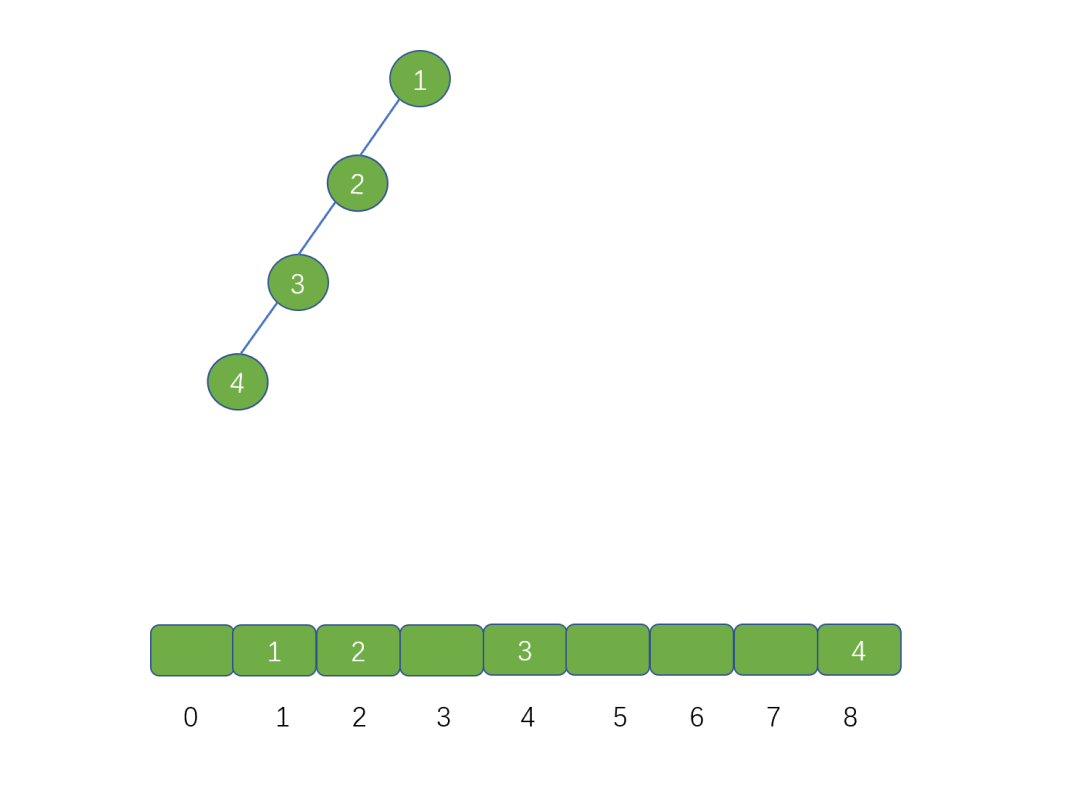
通過 2*i 進行存儲左子節點的話,如果遇到斜樹時,則會浪費很多的存儲空間,這樣顯然是不合適的,
所以說當存儲完全二叉樹時,我們用數組存儲,無疑是最省內存的,但是存儲斜樹時,則就不太合適。
所以我們下面介紹一下另一種存儲結構,鏈式存儲結構。
因為二叉樹的每個節點, 最多有兩個孩子, 所以我們只需為每個節點定義一個數據域,兩個指針域即可
val 為節點的值, left 指向左子節點, right 指向右子節點。

下面我們對樹 1, 2, 3, 4, 5, 6, 7 使用鏈式存儲結構進行存儲,即為下面這種情況。
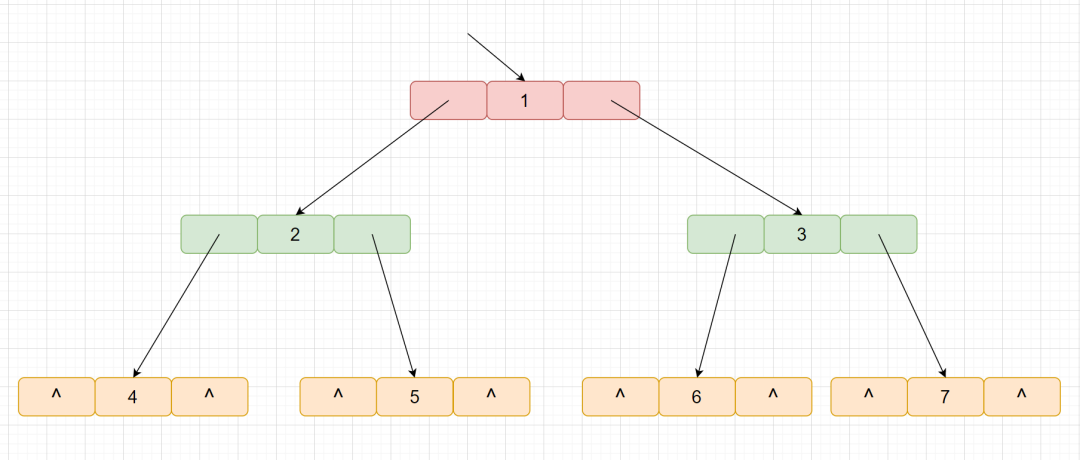
二叉鏈表的節點結構定義代碼
public class BinaryTree {
int val;
BinaryTree left;
BinaryTree right;
BinaryTree() {}
BinaryTree(int val) { this.val = val; }
BinaryTree(int val, BinaryTree left, BinaryTree right) {
this.val = val;
this.left = left;
this.right = right;
}
}
另外我們在刷題的時候, 可以自己實現一下數據結構, 加深我們的理解, 提升基本功, 而且面試考的也越來越多。
好啦,下面我們說一下樹的遍歷,
下面我會用動圖的形式進行描述,很容易理解, 我也會為大家總結對應的題目,歡迎各位閱讀。
遍歷二叉樹
二叉樹的遍歷指從根節點出發,按照某種次序依次訪問二叉樹的所有節點,使得每個節點都被訪問且訪問一次。
我們下面介紹二叉樹的幾種遍歷方法及其對應的題目, 前序遍歷, 中序遍歷 , 后序遍歷 , 層序遍歷 。
前序遍歷
前序遍歷的順序是, 對于樹中的某節點,先遍歷該節點,然后再遍歷其左子樹,最后遍歷其右子樹。
只看文字有點生硬, 下面我們直接看動畫吧
前序遍歷
測試題目: leetcode 144. 二叉樹的前序遍歷
代碼實現(遞歸版)
class Solution {
public List《Integer》 preorderTraversal(TreeNode root) {
List《Integer》 arr = new ArrayList《》();
preorder(root,arr);
return arr;
}
public void preorder(TreeNode root,List《Integer》 arr) {
if (root == null) {
return;
}
arr.add(root.val);
preorder(root.left,arr);
preorder(root.right,arr);
}
}
時間復雜度 : O(n) 空間復雜度 : O(n) 為遞歸過程中棧的開銷,平均為 O(logn),但是當二叉樹為斜樹時則為 O(n)
為了控制文章篇幅, 二叉樹的迭代遍歷形式, 會在下篇文章進行介紹。
中序遍歷
中序遍歷的順序是, 對于樹中的某節點,先遍歷該節點的左子樹, 然后再遍歷該節點, 最后遍歷其右子樹
繼續看動畫吧, 如果有些遺忘或者剛開始學數據結構的同學可以自己模擬一下執行步驟。
中序遍歷
測試題目: leetcode 94 題 二叉樹的中序遍歷
代碼實現(遞歸版)
class Solution {
public List《Integer》 inorderTraversal(TreeNode root) {
List《Integer》 res = new ArrayList《》();
inorder(root, res);
return res;
}
public void inorder (TreeNode root, List《Integer》 res) {
if (root == null) {
return;
}
inorder(root.left, res);
res.add(root.val);
inorder(root.right, res);
}
}
時間復雜度 : O(n) 空間復雜度 : O(n)
后序遍歷
后序遍歷的順序是,對于樹中的某節點, 先遍歷該節點的左子樹, 再遍歷其右子樹, 最后遍歷該節點。
后序遍歷
測試題目: leetcode 145 題 二叉樹的后序遍歷
代碼實現(遞歸版)
class Solution {
public List《Integer》 postorderTraversal(TreeNode root) {
List《Integer》 res = new ArrayList《》();
postorder(root,res);
return res;
}
public void postorder(TreeNode root, List《Integer》 res) {
if (root == null) {
return;
}
postorder(root.left, res);
postorder(root.right, res);
res.add(root.val);
}
}
時間復雜度 : O(n) 空間復雜度 : O(n)
層序遍歷
顧名思義,一層一層的遍歷。
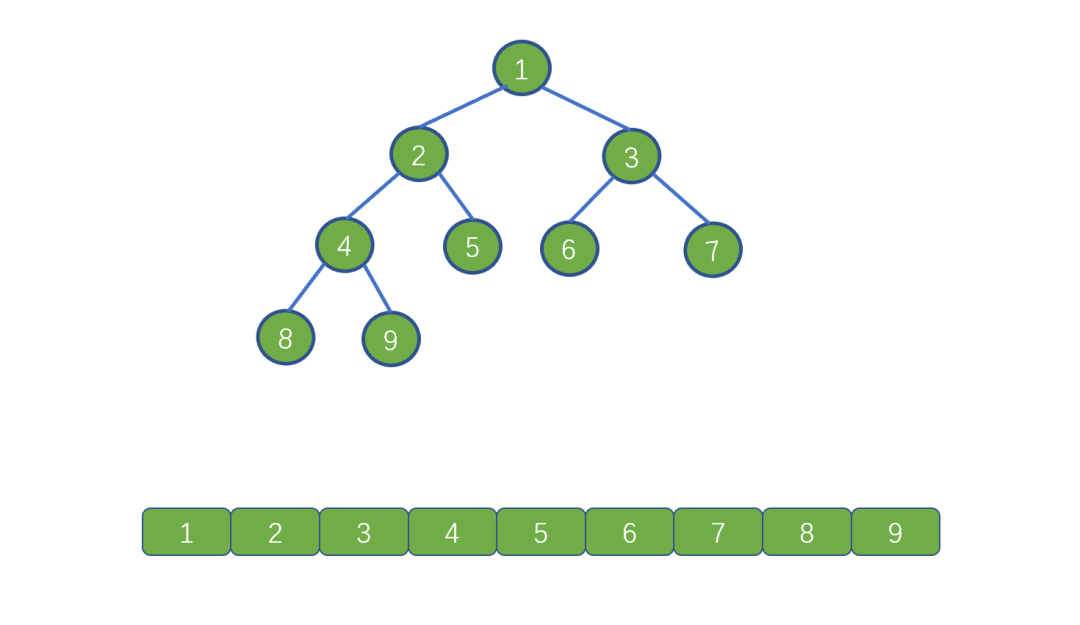
比如剛才那棵二叉樹的層序遍歷序列即為 1 ~ 9.
二叉樹的層序, 這里我們需要借助其他數據結構來實現, 我們思考一下, 我們需要對二叉樹進行層次遍歷, 從上往下進行遍歷, 我們可以借助什么數據結構來幫我們呢 ?
我們可以利用隊列先進先出的特性,使用隊列來幫助我們完成層序遍歷, 具體操作如下
讓二叉樹的每一層入隊, 然后再依次執行出隊操作,
對該層節點執行出隊操作時, 需要將該節點的左孩子節點和右孩子節點進行入隊操作,
這樣當該層的所有節點出隊結束后, 下一層也就入隊完畢,
不過我們需要考慮的就是, 我們需要通過一個變量來保存每一層節點的數量。
這樣做是為了防止, 一直執行出隊操作, 使輸出不能分層,
測試題目: leetcode 102 二叉樹的層序遍歷
題目代碼
class Solution {
public List《List《Integer》》 levelOrder(TreeNode root) {
List《List《Integer》》 res = new ArrayList《》();
if (root == null) {
return res;
}
//入隊 root 節點,也就是第一層
Queue《TreeNode》 queue = new LinkedList《》();
queue.offer(root);
while (!queue.isEmpty()) {
List《Integer》 list = new ArrayList《》();
int size = queue.size();
for (int i = 0; i 《 size; ++i) {
TreeNode temp = queue.poll();
//孩子節點不為空,則入隊
if (temp.left != null) queue.offer(temp.left);
if (temp.right != null) queue.offer(temp.right);
list.add(temp.val);
}
res.add(list);
}
return res;
}
}
時間復雜度:O(n) 空間復雜度:O(n)
大家如果吃透了二叉樹的層序遍歷的話,可以順手把下面幾道題目解決掉,思路一致,甚至都不用拐彎
leetcode 107. 二叉樹的層序遍歷 II
leetcode 103. 二叉樹的鋸齒形層序遍歷上面兩道題僅僅是多了翻轉
leetcode 199. 二叉樹的右視圖
leetcode 515. 在每個樹行中找最大值
leetcode 637. 二叉樹的層平均值
這三道題,僅僅是加了一層的一些操作
leetcode 116 填充每個節點的下一個右側
leetcode 117 填充每個節點的下一個右側2
這兩個題對每一層的節點進行鏈接即可,兩道題目代碼一致
大家可以去順手解決這些題目,但是也要注意一下其他解法,把題目吃透。不要為了數目而刷題,好啦,今天的節目就到這里啦,我們下期見!
原文標題:把二叉樹揉碎(一)
文章出處:【微信公眾號:算法與數據結構】歡迎添加關注!文章轉載請注明出處。
責任編輯:haq
-
數據
+關注
關注
8文章
7030瀏覽量
89035
原文標題:把二叉樹揉碎(一)
文章出處:【微信號:TheAlgorithm,微信公眾號:算法與數據結構】歡迎添加關注!文章轉載請注明出處。
發布評論請先 登錄
相關推薦
DDC264配置寄存器數據寫入和320 DCLK時鐘脈沖后的回讀數據結構是什么?
視覺軟件HALCON的數據結構
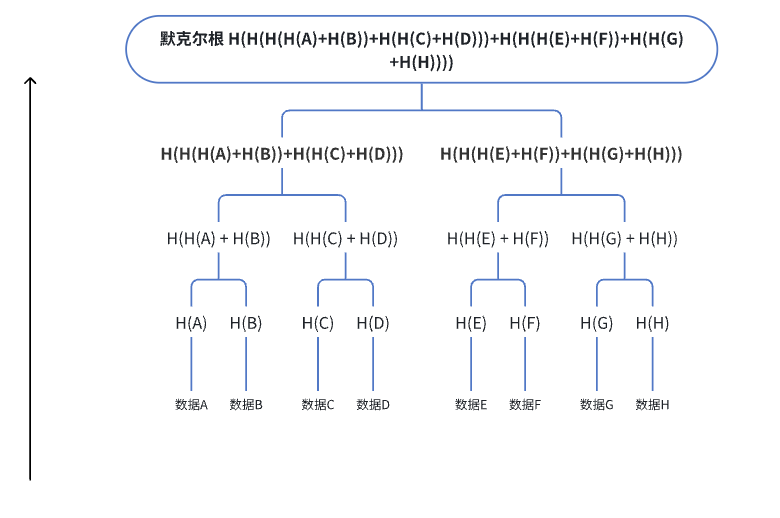
什么是默克爾樹(Merkle Tree)?如何計算默克爾根?
嵌入式常用數據結構有哪些
原理圖設計里兩顆重要的樹(國產EDA)




 新數據結構“樹”的詳細介紹
新數據結構“樹”的詳細介紹













評論