神經網絡知識。
有一種叫做注意機制的東西,但是你不需要知道注意力具體實現。
RNN/LSTM的不足。
A. Vaswani等人的《Attention Is All You Need》被認為是解決了眾所周知的LSTM/RNN體系結構在深度學習空間中的局限性的突破之一。本文介紹了transformers 在seq2seq任務中的應用。該論文巧妙地利用了 D.Bahdanau 等人通過聯合學習對齊和翻譯的神經機器翻譯注意機制的使用。并且提供一些示例明確且詳盡地解釋了注意力機制的數學和應用。
在本文中,我將專注于注意力機制的位置編碼部分及其數學。
假設您正在構建一個 seq2seq 學習任務,并且您想要開發一個模型,該模型將輸入英語句子并將其翻譯成其他 語言。“All animals are equal but some are more equal than others ”→Badhā prā?ī’ō samāna chē parantu kē?alāka an’ya karatā vadhu samāna chē你的第一步是獲取這個輸入句子,運行一個分詞器,將它轉換成數字,然后將它傳遞給一個嵌入層,這可能會為這個句子中的每個單詞添加一個額外的維度。
在運行 RNN 或 LSTM 時,隱藏狀態保留單詞在句子中的相對位置信息。然而,在 Transformer 網絡中,如果編碼器包含一個前饋網絡,那么只傳遞詞嵌入就等于為您的模型增加了不必要的混亂,因為在詞嵌入中沒有捕獲有關句子的順序信息。為了處理單詞相對位置的問題,位置編碼的想法出現了。
在從嵌入層提取詞嵌入后,位置編碼被添加到這個嵌入向量中。
解釋位置編碼最簡單的方法是為每個單詞分配一個唯一的數字 ∈ ? 。或者為每個單詞分配一個在 [0,1] ∈ ? 范圍內的實數(如果輸入句子很長,這樣可以處理很大的值)。但是,上述兩種方法都沒有捕捉到單詞之間時間步長的準確性。為了克服這個問題,本文使用了 sin 和 cosine 函數形式的位置編碼。
打個比方,我們輸入模型的序列,無論是句子、視頻序列還是股票市場價格數據,都將始終是時域信號。表示時域信號的最佳方式是通過正弦方程 sin(ωt)。如果我們巧妙地使用這個波動方程,我們可以在一次拍攝中捕獲詞嵌入的時間和維度信息。
讓我們看一下這個等式,在接下來的步驟中,我們將嘗試把它形象化。
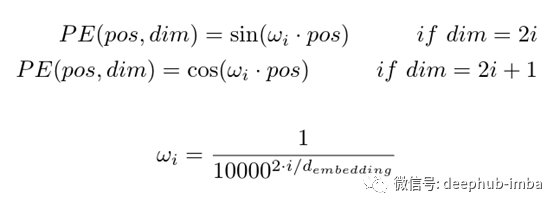
讓我們考慮一個簡單的句子,它被分詞,然后它的詞嵌入被提取。句子長度為5,嵌入維數為8。因此,每個單詞都表示為1x8的向量。
現在我們在時間維度上取一個序列把正弦PE向量加到這個嵌入向量上。
進一步,我們對沿dim維數的其他向量做類似的操作。
本文在嵌入向量中交替加入正弦和余弦。如果dim是偶數,則sin級數相加,如果dim是奇數,則cos級數相加。
這很好地捕獲了沿時間維度(或等式中描述的 pos 維度。我將 pos 和 time 互換使用,因為它們意味著相同的事情)但是如何也捕獲沿dims維度的相對位置信息呢?這里的答案也在于等式本身。ω 項。
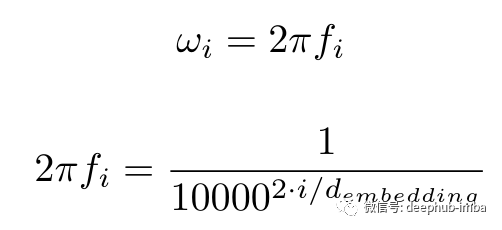
隨著 i 從 0 增加到 d_embedding/2,頻率也從 1/2π 減少到 1/(2π.10000)
因此我們看到,沿著無序方向的每個向量,位置的唯一性被捕獲。該論文還描述了這種編碼的魯棒性。但是我仍然無法找出為什么特別使用數字 10000 進行位置編碼(它可能是一個超參數嗎?)。這個解釋粗略地展示了如何使用正弦和余弦對于模型理解是非常合理和有效的。下面的圖表本身講述了位置編碼如何隨位置(時間)和尺寸變化。
人們可以很容易地看到,這些是簡單的時頻圖,其中位置代表時間,深度代表頻率。時間頻率圖已被用于從射電天文學到材料光譜分析的許多應用中。因此,從現有的現實世界系統構建類比確實可以更好地理解問題。
這是我對注意力機制中使用的位置編碼的看法。在接下來的系列中,我將嘗試撰寫有關編碼器-解碼器部分的內容,并將注意力應用于現實世界的規模問題。
編輯:jq
-
神經網絡
+關注
關注
42文章
4773瀏覽量
100890 -
編碼
+關注
關注
6文章
946瀏覽量
54870 -
rnn
+關注
關注
0文章
89瀏覽量
6895 -
LSTM
+關注
關注
0文章
59瀏覽量
3767
原文標題:位置編碼在注意機制中的作用
文章出處:【微信號:zenRRan,微信公眾號:深度學習自然語言處理】歡迎添加關注!文章轉載請注明出處。
發布評論請先 登錄
相關推薦




 簡述位置編碼在注意機制中的作用
簡述位置編碼在注意機制中的作用













評論