前文指出了基于系統滴答計數實現的毫秒級延時的問題。
uint32_t comm_get_ms(void)
{
return sys_tick_get();
}
void comm_delay(uint32_t ms)
{
uint32_t timeout = comm_get_ms() + ms;
while(comm_get_ms() 《 timeout);
}
comm_get_ms返回當前系統時間(系統滴答計數),即系統從啟動到現在經過了多少毫秒。comm_delay先獲取當前時間,加上延時時間以計算出到期時間timeout,之后循環等待當前時間超過timeout以完成延時。
系統時間使用uint32_t變量來記錄,經過49.71天后將達到最大值UINT32_MAX(0xffffffff),溢出后回到0重新累加。不僅是當前時間會溢出,在接近49.71天時,計算的timeout將會更先一步溢出,從而使延時判斷失效。
前文在結尾給出了解決方案:
void comm_delay(uint32_t ms)
{
uint32_t timeout = comm_get_ms() + ms;
while(comm_get_ms() - timeout 》 UINT32_MAX / 2);
}
其實改動很小,僅僅修改了判斷超時的條件。為什么要用兩個時間差去與UINT32_MAX / 2比較?判斷條件為什么是大于?
了解其中的原理是有必要的。因為延時的條件如上,而如果想實現定時的話,條件就會倒過來。知其所以然,方能靈活運用。
定時任務:
uint32_t timeout = 0;
while (1)
{
if (comm_get_ms() - timeout 《 UINT32_MAX / 2)
{
printf(“hello
”);
timeout = comm_get_ms() + 1000;
}
}
主要矛盾
無論是延時還是定時,我們都是在進行時間的比較。先根據延時或定時時長計算出到期時間timeout,之后不停的判斷當時時間有沒有超過這個timeout。
所有的時間變量都是uint32_t,由于它的最大值非常大,為了方便講解,我們假設所有的變量都是uint8_t,即8位無符號整型,取值范圍為0-255。同樣為方便敘述,以cur_time表示當前時間,以timeout表示目標到期時間。
現在的任務也非常清楚了,在各種場景下比較cur_time是否超過了timeout。比如:
起始cur_time為10,延時目標為5,則timeout為10 + 5 = 15。判斷依據非常簡單,cur_time 《 15時視為未超過timeout,或者說cur_time 《 timeout視為未超過timeout。
起始cur_time為250,延時目標為10,則timeout為250 + 10 = 260 = 4。此時cur_time 《 timeout不再適用。
張三和李四誰跑的快
既然時間溢出問題讓我們頭疼,那我們先來看一個簡單的問題,一個任何人都可以不假思索得出答案的問題:判斷跑道上的張三和李四誰跑的快,或者說誰跑在前面。
如下圖,張三(A)和李四(B)在跑道上跑步,沿逆時針方向跑。藍色是起跑線,不過他們并不只跑一圈,假設跑三圈。并且我們知道,張三和李四的水平相差不大,短短的三圈不足以讓他們拉快過長的距離,更不可能出現套圈。
假設這個跑道長256米,從起點開始沿逆時針方向(即跑步的方向)標注坐標。那么A和B在坐標軸的位置大致如下:

假設A為10,B為240,A 《 B,但是從跑道的圖中大家不假思索就得出A跑在前面。這是為什么呢?
大家在判斷誰在前面時,其實根本沒去管那根藍色的線(起點或終點)。因為跑道首尾相連,而且張三和李四要跑好幾圈,必將多次經過起終點,所以起終點沒有任何判斷價值。
人腦是怎么判斷的
筆者反復自我剖析,覺得可能是這樣判斷的:
人腦會做兩種假設,張三(A)快,或者李四(B)快。最終選擇一個最合理的假設。
假設張三(A)快,那么A沿順時針跑回B(逆時針是前進方向,往回跑就是順時針)的距離即為A超前B的距離,如下圖的紅色箭頭,相對于一圈的長度而言是一個較小的距離。假設李四(B)快,則B沿順時針方向需要跑大半圈才能遇到張三(A)。如果李四確實比張三快的話,那么快了不只一點點,而是超前大半圈。先前說過,張三和李四的水平相差不大,短短的三圈不足以讓他們拉快過長的距離。所以我們更愿意相信第一種假設成立,即張三(A)比李四(B)跑的快。
人腦做上述判斷的時候,并沒有給跑道建立坐標系,也不是判斷張三和李四的坐標值哪個大,而是判斷張三和李四的距離。這個距離是有方向性的。
假設張三(A)快,則目測A跑回B的距離L(A-B)。這個距離比較小,所以判斷成立,A確實在B前面。
假設李四(B)快,則目測B跑回A的距離L(B-A)。這個距離比較大,所以判斷不成立,B其實在A的后面。
其實根本不需要驗證兩種假設,只需要驗證一個就行了,因為它們是對立的。
回歸代碼
人腦通過視覺來估測張三與李四的距離,但是計算機不行,它需要一個明確的方法,還是需要坐標系的。
還是假設這個跑道長256米,從起點開始沿逆時針方向(即跑步的方向)標注坐標。
簡單情況
先看簡單的情況,即A和B在起點的同側。對應到坐標系上為:

A在40米處(記為Xa),B在20米處(記為Xb)。A返回到B的距離為
L = Xa - Xb = 40 - 20 = 20
這個距離遠小于256,所以A在B的前面。
溢出情況
再來看看復雜的溢出情況,即A和B在起點兩側。
對應在坐標系上時,為方便繪制,將A、B與起終點的距離拉遠一點。Xa=30,Xb=220。A返回到B的距離為:
L = L1 + L2 = (Xa - 0) + (256 - Xb) = 30 + (256 - 220) = 66
66也是遠小于256的,所以A還是在B的前面。
歸一
有沒有發現什么不對?剛才討論區分簡單情況和溢出情況,在計算L時的公式是不同的,這可有點小麻煩。如果有統一的公式就好了。
讓我們再看一眼溢出情況的公式:
L = L1 + L2
= (Xa - 0) + (256 - Xb)
= Xa - Xb + 256 = Xa - Xb
這么一調整就和簡單情況一樣了吧。為什么把加256給去掉了?因為我們討論Xa和Xb是uint8_t,加256和沒加是一樣的。
驗證
還是上一個例子的場景,我們來假設B在A前面。B返回到A的距離為:
L = Xb - Xa = 220 - 30 = 190
190比較接近256,所以假設不成立,B并不在A前面,而是A在B前面。
我們在判斷距離時,用了兩種標準:
L遠小于256
L比較接近256
對于計算機而言,這是無法實現的,它需要一個明確的標準。那是什么呢?就一刀切吧,以256 / 2為閾值。
L 《 256 / 2:假設成立
L 》 256 / 2:假設失敗至于L == 256 / 2的情況,隨便歸入哪個都行。
再看時間判斷
void comm_delay(uint32_t ms)
{
uint32_t timeout = comm_get_ms() + ms;
while(comm_get_ms() - timeout 》 UINT32_MAX / 2);
}
再看這時間判斷,有沒有豁然開朗呢?comm_get_ms()是張三,timeout是李四,變量范圍由uint8_t變成了uint32_t,僅此而已。
后記
這種超時判斷方法并非由筆者想出,是筆者在閱讀RT-Thead操作系統的timer源碼時發現的。rt_timer是RT-Thread的定時器模塊,提供基于系統滴答計數的定時功能,其計數值就是32位無符號整型uint32_t,時間久了必然溢出。
筆者之前也為溢出問題感到頭疼,而RT-Thread號稱不懼溢出,于是筆者懷著好奇的心態挖掘了其解決方法。在rt_timer中,有多處這樣的判斷,現在看起來是不是感覺很親切呢?
/*
* It supposes that the new tick shall less than the half duration of
* tick max.
*/if ((current_tick - t-》timeout_tick) 《 RT_TICK_MAX / 2)
編輯:jq
-
延時
+關注
關注
0文章
107瀏覽量
25535
原文標題:從rtthread timer模塊中找到裸機定時問題的解決方案
文章出處:【微信號:LinuxDev,微信公眾號:Linux閱碼場】歡迎添加關注!文章轉載請注明出處。
發布評論請先 登錄
相關推薦
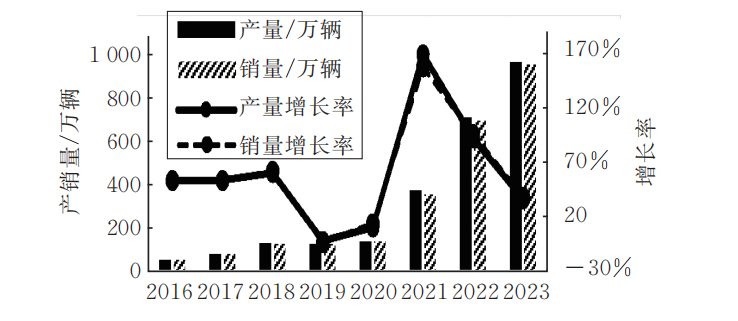
淺探電動汽車火災事故剖析與防控策略探究
用TLV320AIC3101配DM368的開發板做交互通話,音頻延時能調到最低多少毫秒?
請問PurePath Studio有定時器控件嗎?用AIC3254如何實現毫秒級的定時?
AIC3254可以把mic采集到的音頻相位調整180度再延時1毫秒輸出給揚聲器?
延時開關上l和a是什么意思
實現一個ns級的延時函數,延時時間不可控的原因?
使用定時器的編碼器接口模式,打開定時器的溢出中斷,當定時器上溢出和下溢出是,是否都會產生溢出中斷?
求助,關于系統嘀嗒時鐘溢出問題求解
stm32cubemx的HAL_Delay()函數,當HAL_GetTick()的計數正好要溢出時,是不是延時就不準了?
AI垃圾溢出識別攝像機





 剖析毫秒級延時防溢出的原理
剖析毫秒級延時防溢出的原理











評論