我們在生活中做出的許多決定都是基于其他人的意見,而通常情況下由一群人做出的決策比由該群體中的任何一個成員做出的決策會產生更好的結果,這被稱為群體的智慧。集成學習(Ensemble Learning)類似于這種思想,集成學習結合了來自多個模型的預測,旨在比集成該學習器的任何成員表現得更好,從而提升預測性能(模型的準確率),預測性能也是許多分類和回歸問題的最重要的關注點。
集成學習(Ensemble Learning)是將若干個弱分類器(也可以是回歸器)組合從而產生一個新的分類器。(弱分類器是指分類準確率略好于隨機猜想的分類器,即error rate 《 0.5)。
集成機器學習涉及結合來自多個熟練模型的預測,該算法的成功在于保證弱分類器的多樣性。而且集成不穩定的算法也能夠得到一個比較明顯的性能提升。集成學習是一種思想。當預測建模項目的最佳性能是最重要的結果時,集成學習方法很受歡迎,通常是首選技術。
為什么要使用集成學習?
(1) 性能更好:與任何單個模型的貢獻相比,集成可以做出更好的預測并獲得更好的性能;
(2) 魯棒性更強:集成減少了預測和模型性能的傳播或分散,平滑了模型的預期性能。
(3) 更加合理的邊界:弱分類器間存在一定差異性,導致分類的邊界不同。多個弱分類器合并后,就可以得到更加合理的邊界,減少整體的錯誤率,實現更好的效果;
(4) 適應不同樣本體量:對于樣本的過大或者過小,可分別進行劃分和有放回的操作產生不同的樣本子集,再使用樣本子集訓練不同的分類器,最后進行合并;
(5) 易于融合:對于多個異構特征數據集,很難進行融合,可以對每個數據集進行建模,再進行模型融合。
機器學習建模的偏差和方差
機器學習模型產生的錯誤通常用兩個屬性來描述:偏差和方差。
偏差是衡量模型可以捕獲輸入和輸出之間的映射函數的接近程度。它捕獲了模型的剛性:模型對輸入和輸出之間映射的函數形式的假設強度。
模型的方差是模型在擬合不同訓練數據時的性能變化量。它捕獲數據的細節對模型的影響。
理想情況下,我們更喜歡低偏差和低方差的模型,事實上,這也是針對給定的預測建模問題應用機器學習的目標。模型性能的偏差和方差是相關的,減少偏差通常可以通過增加方差來輕松實現。相反,通過增加偏差可以很容易地減少方差。
與單個預測模型相比,集成用在預測建模問題上實現更好的預測性能。實現這一點的方式可以理解為模型通過添加偏差來減少預測誤差的方差分量(即權衡偏差-方差的情況下)。
集成學習之Bagging思想
Bagging又稱自舉匯聚法(Bootstrap Aggregating),涉及在同一數據集的不同樣本上擬合許多學習器并對預測進行平均,通過改變訓練數據來尋找多樣化的集成成員。
Bagging思想就是在原始數據集上通過有放回的抽樣,重新選擇出N個新數據集來分別訓練N個分類器的集成技術。模型訓練數據中允許存在重復數據。
使用Bagging方法訓練出來的模型在預測新樣本分類的時候,會使用多數投票或者取平均值的策略來統計最終的分類結果。
基于Bagging的弱學習器(分類器/回歸器)可以是基本的算法模型,如Linear、Ridge、Lasso、Logistic、Softmax、ID3、C4.5、CART、SVM、KNN、Naive Bayes等。
隨機森林 (Random Forest)
1. 隨機森林算法原理
隨機森林是在Bagging策略的基礎上進行修改后的一種算法,方法如下:(1) 使用Bootstrap策略從樣本集中進行數據采樣;(2) 從所有特征中隨機選擇K個特征,構建正常決策樹;(3) 重復1,2多次,構建多棵決策樹;(4) 集成多棵決策樹,形成隨機森林,通過投票表決或取平均值對數據進行決策。
2. 隨機森林OOB Error
在隨機森林中可以發現Bootstrap采樣每次約有1/3的樣本不會出現在Bootstrap所采樣的樣本集合中,當然也沒有參加決策樹的建立,而這部分數據稱之為袋外數據OOB(out of bag),它可以用于取代測試集誤差估計方法。
對于已經生成的隨機森林,用袋外數據測試其性能,假設袋外數據總數為O,用這O個袋外數據作為輸入,帶進之前已經生成的隨機森林分類器,分類器會給出O個數據相應的分類,因為這O條數據的類型是已知的,則用正確的分類與隨機森林分類器的結果進行比較,統計隨機森林分類器分類錯誤的數目,設為X,則袋外數據誤差大小為X/O。
優點:這已經經過證明是無偏估計的,所以在隨機森林算法中不需要再進行交叉驗證或者單獨的測試集來獲取測試集誤差的無偏估計。
缺點:當數據量較小時,Bootstrap采樣產生的數據集改變了初始數據集的分布,這會引入估計偏差。
隨機森林算法變種
RF算法在實際應用中具有比較好的特性,應用也比較廣泛,主要應用在:分類、歸回、特征轉換、異常點檢測等。
以下為常見的RF變種算法:
Extra Trees (ET)
Totally Random Trees Embedding (TRTE)
Isolation Forest (IForest)
1. Extra Trees (ET)
Extra-Trees(Extremely randomized trees,極端隨機樹)是由Pierre Geurts等人于2006年提出。是RF的一個變種,原理基本和RF一樣。
但該算法與隨機森林有兩點主要的區別:(1) 隨機森林會使用Bootstrap進行隨機采樣,作為子決策樹的訓練集,應用的是Bagging模型;而ET使用所有的訓練樣本對每棵子樹進行訓練,也就是ET的每個子決策樹采用原始樣本訓練;(2) 隨機森林在選擇劃分特征點的時候會和傳統決策樹一樣(基于信息增益、信息增益率、基尼系數、均方差等),而ET是完全隨機的選擇劃分特征來劃分決策樹。
對于某棵決策樹,由于它的最佳劃分特征是隨機選擇的,因此它的預測結果往往是不準確的,但是多棵決策樹組合在一起,就可以達到很好的預測效果。
當ET構建完成,我們也可以應用全部訓練樣本得到該ET的誤差。因為盡管構建決策樹和預測應用的都是同一個訓練樣本集,但由于最佳劃分屬性是隨機選擇的,所以我們仍然會得到完全不同的預測結果,用該預測結果就可以與樣本的真實響應值比較,從而得到預測誤差。如果與隨機森林相類比的話,在ET中,全部訓練樣本都是OOB樣本,所以計算ET的預測誤差,也就是計算這個OOB誤差。
由于Extra Trees是隨機選擇特征值的劃分點,會導致決策樹的規模一般大于RF所生成的決策樹。也就是說Extra Trees模型的方差相對于RF進一步減少。在某些情況下,ET具有比隨機森林更強的泛化能力。
2. Totally Random Trees Embedding (TRTE)
TRTE是一種非監督學習的數據轉化方式。它將低維的數據映射到高維,從而讓映射到高維的數據更好的應用于分類回歸模型。
TRTE算法的轉換過程類似RF算法的方法,建立T個決策樹來擬合數據。當決策樹構建完成后,數據集里的每個數據在T個決策子樹中葉子節點的位置就定下來了,將位置信息轉換為向量就完成了特征轉換操作。
例如,有3棵決策樹,每棵決策樹有5個葉子節點,某個數據特征x劃分到第一個決策樹的第3個葉子節點,第二個決策樹的第1個葉子節點,第三個決策樹的第5個葉子節點。則x映射后的特征編碼為(0,0,1,0,0 1,0,0,0,0 0,0,0,0,1),有15維的高維特征。特征映射到高維之后,就可以進一步進行監督學習。
3. Isolation Forest (IForest)IForest是一種異常點檢測算法,使用類似RF的方式來檢測異常點。
IForest算法和RF算法的區別在于:
(1) 在隨機采樣的過程中,一般只需要少量數據即可;
(2) 在進行決策樹構建過程中,IForest算法會隨機選擇一個劃分特征,并對劃分特征隨機選擇一個劃分閾值;
(3) IForest算法構建的決策樹一般深度max_depth是比較小的。
IForest的目的是異常點檢測,所以只要能夠區分異常數據即可,不需要大量數據;另外在異常點檢測的過程中,一般不需要太大規模的決策樹。
對于異常點的判斷,則是將測試樣本x擬合到T棵決策樹上。計算在每棵樹上該樣本的葉子結點的深度ht(x)。從而計算出平均深度h(x);然后就可以使用下列公式計算樣本點x的異常概率值,p(s,m)的取值范圍為[0,1],越接近于1,則是異常點的概率越大。
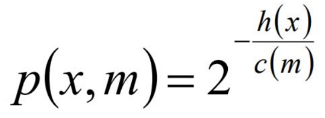
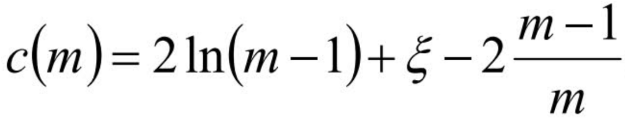
m為樣本個數,ξ 為歐拉常數
隨機森林優缺點總結
本文我們一起了解了Bagging思想及其原理,以及基于Bagging的隨機森林相關知識。最后,讓我們一起總結下隨機森林的優缺點:
優點
訓練可以并行化,對于大規模樣本的訓練具有速度的優勢;
由于進行隨機選擇決策樹劃分特征列表,這樣在樣本維度比較高的時候,仍然具有比較好的訓練性能;
由于存在隨機抽樣,訓練出來的模型方差小,泛化能力強;
實現簡單;
對于部分特征缺失不敏感;
可以衡量特征的重要性。
缺點
在某些噪聲比較大的特征上,易過擬合;
取值比較多的劃分特征對RF的決策會產生更大的影響,從而有可能影響模型的效果。
編輯:jq
-
集成學習
+關注
關注
0文章
10瀏覽量
7321 -
分類器
+關注
關注
0文章
152瀏覽量
13183 -
數據采樣
+關注
關注
0文章
9瀏覽量
6661
原文標題:機器學習建模中的Bagging思想
文章出處:【微信號:sessdw,微信公眾號:三星半導體互動平臺】歡迎添加關注!文章轉載請注明出處。
發布評論請先 登錄
相關推薦
如何選擇云原生機器學習平臺
Arm成功將Arm KleidiAI軟件庫集成到騰訊自研的Angel 機器學習框架
什么是機器學習?通過機器學習方法能解決哪些問題?

NPU與機器學習算法的關系
eda在機器學習中的應用
人工智能、機器學習和深度學習存在什么區別

人工智能、機器學習和深度學習是什么
機器學習算法原理詳解
深度學習與傳統機器學習的對比
機器學習模型偏差與方差詳解

英飛凌科技旗下Imagimob可視化Graph UX改變邊緣機器學習建模




 為什么要使用集成學習 機器學習建模的偏差和方差
為什么要使用集成學習 機器學習建模的偏差和方差











評論