原始結構的RNN還不夠處理較為復雜的序列建模問題,它存在較為嚴重的梯度消失問題,最直觀的現象就是隨著網絡層數增加,網絡會逐漸變得無法訓練。長短期記憶網絡(Long Short Time Memory,LSTM)正是為了解決梯度消失問題而設計的一種特殊的RNN結構。
深度神經網絡的困擾:梯度爆炸與梯度消失
在此前的普通深度神經網絡和深度卷積網絡的講解時,圖1就是一個簡單的兩層普通網絡,但當網絡結構變深時,神經網絡在訓練時碰到梯度爆炸或者梯度消失的情況。那么什么是梯度爆炸和梯度消失呢?它們又是怎樣產生的?
鑒于神經網絡的訓練機制,不管是哪種類型的神經網絡,其訓練都是通過反向傳播計算梯度來實現權重更新的。通過設定損失函數,建立損失函數關于各層網絡輸入輸出的梯度計算,當網絡訓練開動起來的時候,系統便按照反向傳播機制來不斷更新網絡各層參數直到停止訓練。但當網絡層數加深時,這個訓練系統并不是很穩,經常會出現一些問題。其中梯度爆炸和梯度消失便是較為嚴重的兩個問題。
所謂梯度爆炸就是在神經網絡訓練過程中,梯度變得越來越大以使得神經網絡權重得到瘋狂更新的情形,這種情況很容易發現,因為梯度過大,計算更新得到的參數也會大到崩潰,這時候我們可能看到更新的參數值中有很多的NaN,這說明梯度爆炸已經使得參數更新出現數值溢出。這便是梯度爆炸的基本情況。
然后是梯度消失。與梯度爆炸相反的是,梯度消失就是在神經網絡訓練過程中梯度變得越來越小以至于梯度得不到更新的一種情形。當網絡加深時,網絡深處的誤差很難因為梯度的減小很難影響到前層網絡的權重更新,一旦權重得不到有效的更新計算,神經網絡的訓練機制也就失效了。
為什么神經網絡訓練過程中梯度怎么就會變得越來越大或者越來越小?可以用本書第一講的神經網絡反向傳播推導公式為例來解釋。
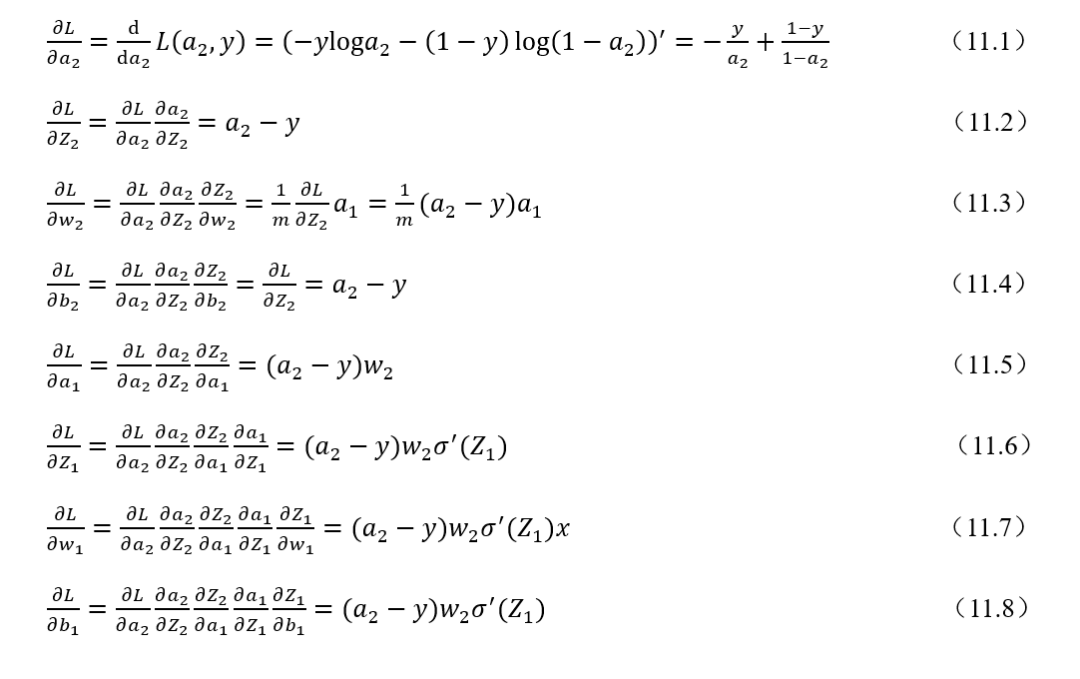
式(11.1)~-式(11.8)是一個兩層網絡的反向傳播參數更新公式推導過程。離輸出層相對較遠的是輸入到隱藏層的權重參數,可以看到損失函數對于隱藏層輸出輸入到隱藏層權重和偏置的梯度計算公式,一般而言都會轉換從下一層的權重乘以激活函數求導后的式子。如果激活函數求導后的結果和下一層權重的乘積大于1或者說遠遠大于1的話,在網絡層數加深時,層層遞增的網絡在做梯度更新時往往就會出現梯度爆炸的情況。如果激活函數求導和下一層權重的乘積小于1的話,在網絡加深時,淺層的網絡梯度計算結果會越來越小往往就會出現梯度消失的情況。所以可是說是反向傳播的機制本身造就梯度爆炸和梯度消失這兩種不穩定因素。例如,一個100層的深度神經網絡,假設每一層的梯度計算值都為1.1,經過由輸出到輸入的反向傳播梯度計算可能最后的梯度值就變成= 13780.61234,這是一個極大的梯度值了,足以造成計算溢出問題。若是每一層的梯度計算值為 0.9,反向傳播輸入層的梯度計算值則可能為= 0.000026561398,足夠小到造成梯度消失。本例只是一個簡化的假設情況,實際反向傳播計算要更為復雜。
所以總體來說,神經網絡的訓練中梯度過大或者過小引起的參數過大過小都會導致神經網絡失效,那我們的目的就是要讓梯度計算回歸到正常的區間范圍,不要過大也不要過小,這也是解決這兩個問題的一個思路。
那么如何解決梯度爆炸和梯度消失問題?梯度爆炸較為容易處理,在實際訓練的時候對梯度進行修剪即可,但是梯度消失的處理就比較麻煩了,由上述的分析我們知道梯度消失一個關鍵在于激活函數。Sigmoid激活函數本身就更容易產生這種問題,所以一般而言,我們換上更加魯棒的ReLu激活函數以及給神經網絡加上歸一化激活函數層(BN層),一般問題都能得到很好的解決,但也不是任何情形下都管用,例如,RNN網絡,具體在下文中我們再做集中探討。
以上便是梯度爆炸和梯度消失這兩種問題的基本解釋,下面我們回歸正題,來談談本文的主角——LSTM。
LSTM:讓RNN具備更好的記憶機制
前面說了很多鋪墊,全部都是為了來講LSTM。梯度爆炸和梯度消失,普通神經網絡和卷積神經網絡有,那么循環神經網絡RNN也有嗎?必須有。而且梯度消失和梯度爆炸的問題之于RNN來說傷害更大。當RNN網絡加深時,因為梯度消失的問題使得前層的網絡權重得不到更新,RNN就會在一定程度上丟失記憶性。為此,在傳統的RNN網絡結構基礎上,研究人員給出一些著名的改進方案,因為這些改進方案都脫離不了經典的RNN架構,所以一般來說我們也稱這些改進方案為RNN變種網絡。比較著名的就是GRU(循環門控單元)和LSTM(長短期記憶網絡)。GRU和LSTM二者結構基本一致,但有部分不同的地方,本講以更有代表性的LSTM來進行詳解。
在正式深入LSTM的技術細節之前,先要明確幾點。第一,LSTM的本質是一種RNN網絡。第二,LSTM在傳統的RNN結構上做了相對復雜的改進,這些改進使得LSTM相對于經典RNN能夠很好的解決梯度爆炸和梯度消失問題,讓循環神經網絡具備更強更好的記憶性能,這也是LSTM的價值所在。那咱們就來重點看一下LSTM的技術細節。
咱們先擺一張經典RNN結構與LSTM結構對比圖,這樣能夠有一個宏觀的把握,然后再針對LSTM結構圖中各個部分進行拆解分析。圖2所示是標準RNN結構,圖3所示是LSTM結構。
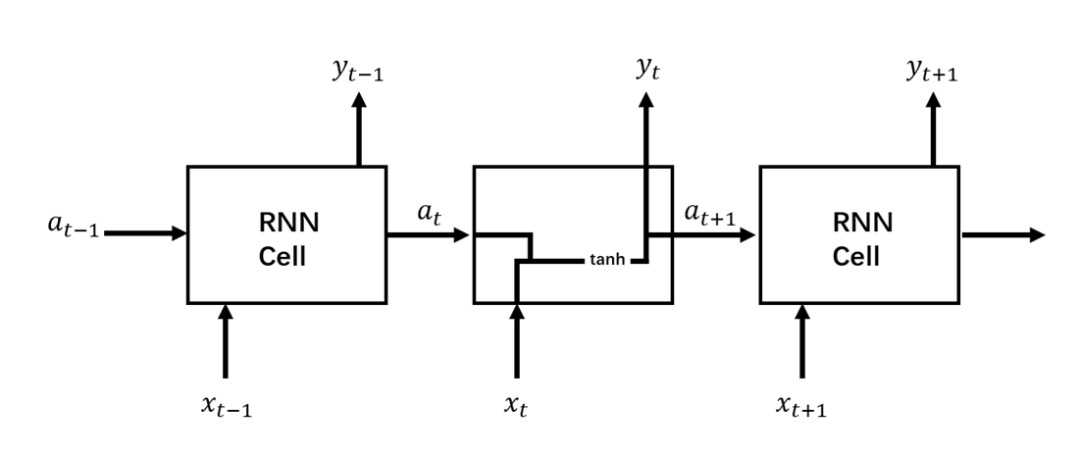
圖2 RNN結構
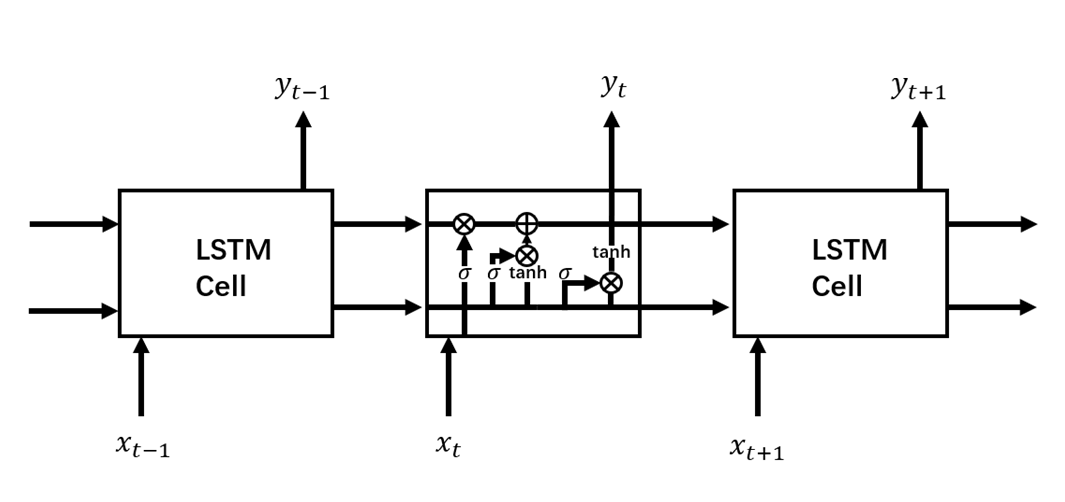
圖3 LSTM結構
從圖3中可以看到,相較于RNN單元,LSTM單元要復雜許多。每個LSTM單元中包含了4個交互的網絡層,現在將LSTM單元放大,并標注上各個結構名稱,如圖4所示。
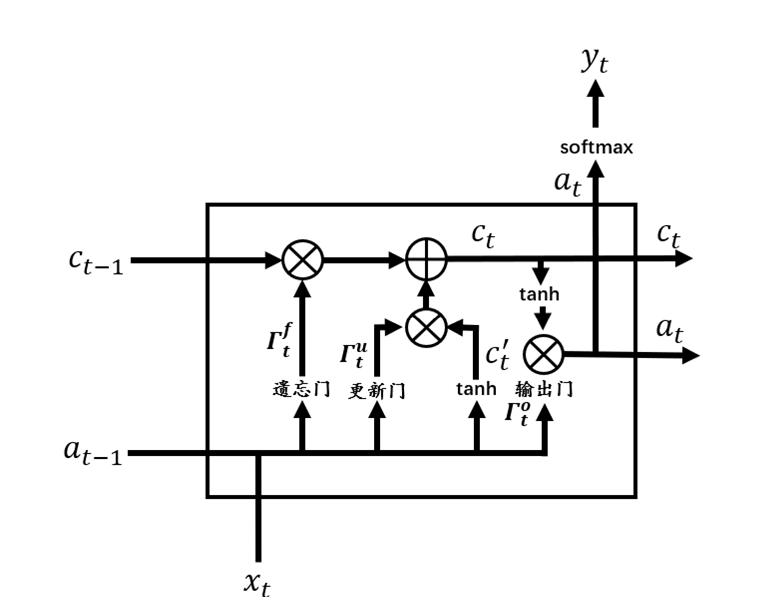
圖4 LSTM單元
根據圖4,一個完整的LSTM單元可以用式(11.9)~(11.14)來表示,其中符號表示兩個向量合并。
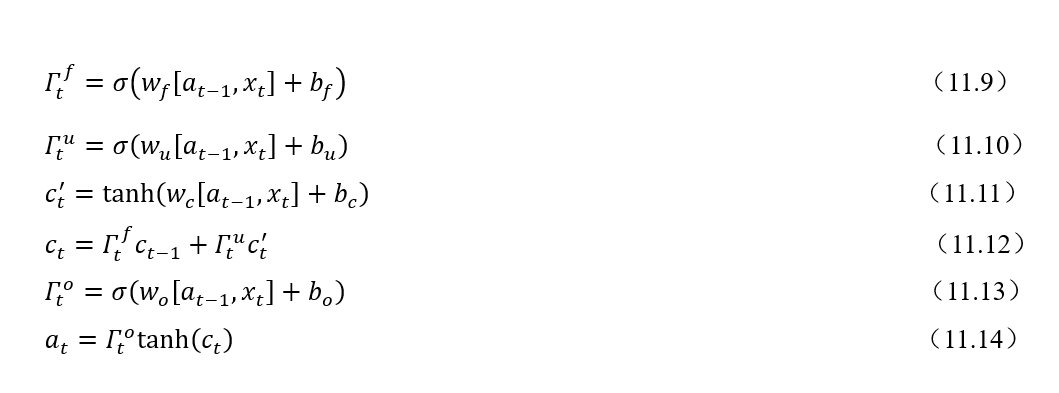
現在我們將LSTM單元結構圖進行分解,根據結構圖和公式來逐模塊解釋LSTM。
1. 記憶細胞
如圖5紅色部分所示,可以看到在LSTM單元的最上面部分有一條貫穿的箭頭直線,這條直線由輸入到輸出,相較于RNN,LSTM提供了c作為記憶細胞輸入。記憶細胞提供了記憶的功能,在網絡結構加深時仍能傳遞前后層的網絡信息。這樣貫穿的直線使得記憶信息在網絡各層之間保持下去很容易。
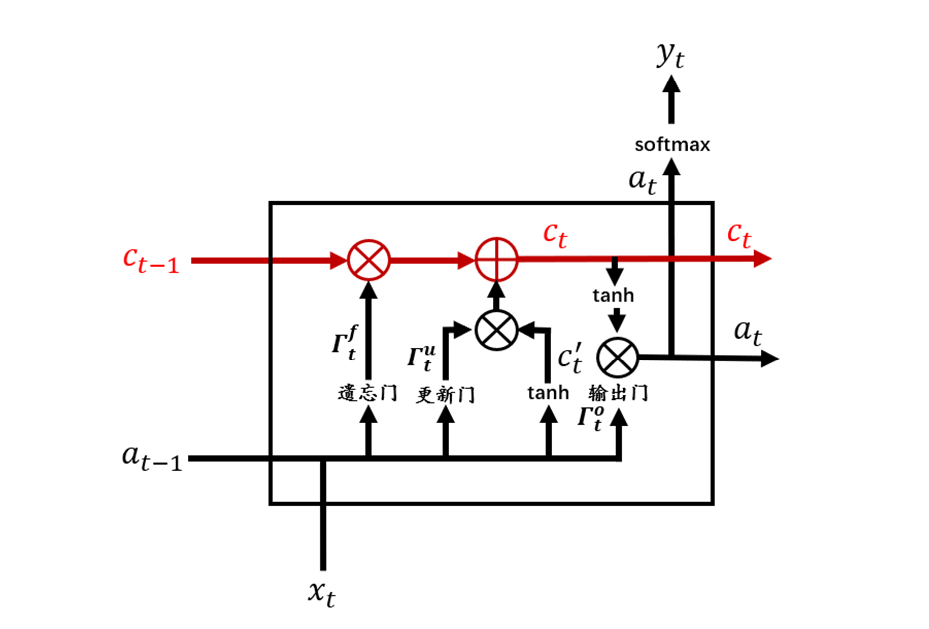
圖5 LSTM記憶細胞
2. 遺忘門(Forget Gate)
遺忘門的計算公式如下:
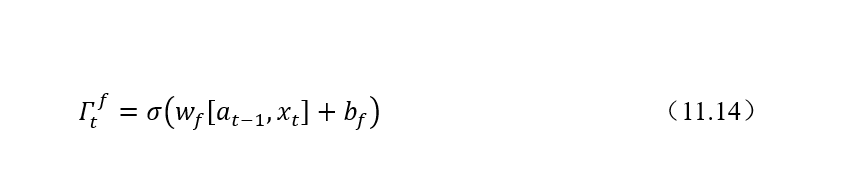
遺忘門的作用是要決定從記憶細胞c中是否丟棄某些信息,這個過程可以通過一個 Sigmoid函數來進行處理。遺忘門在整個結構中的位置如圖11.6所示。可以看到,遺忘門接受來自輸入和上一層隱狀態的值進行合并后加權計算處理。
3. 記憶細胞候選值和更新門
更新門(Update Gate)表示需要將什么樣的信息能存入記憶細胞中。除了計算更新門之外,還需要使用tanh計算記憶細胞的候選值。LSTM中更新門需要更加細心一點。記憶細胞候選值和更新門的計算公式如下:
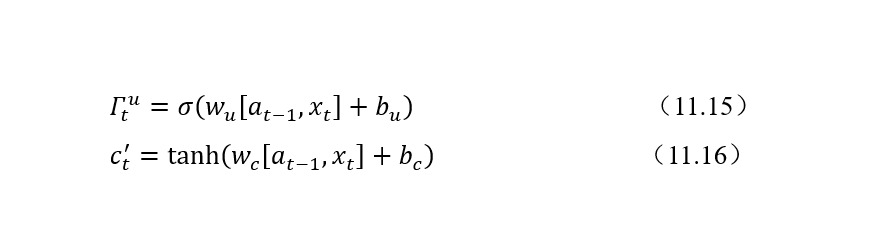
更新門和tanh在整個結構中的位置如圖7所示。
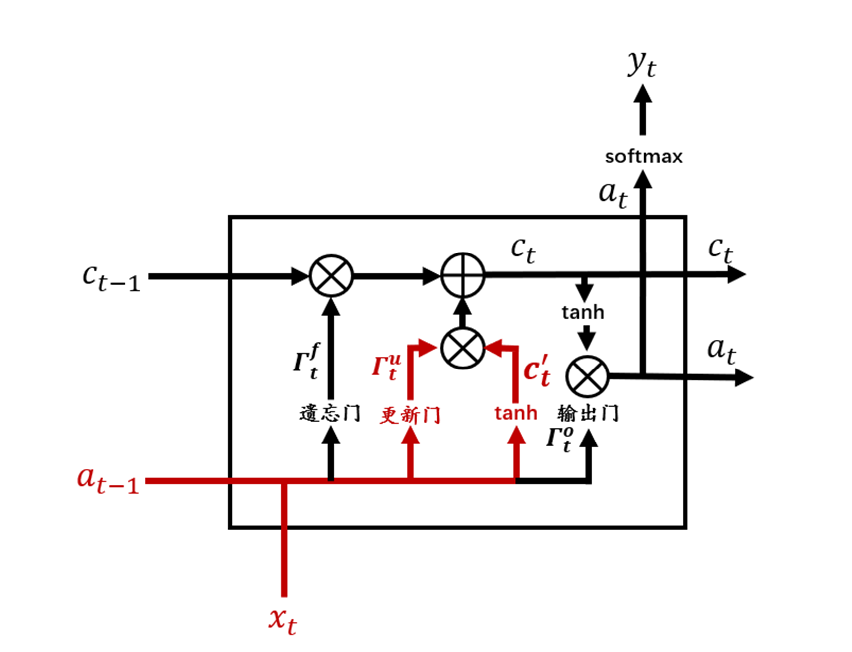
圖7 記憶細胞候選值和更新門
4. 記憶細胞更新
結合遺忘門、更新門、上一個單元記憶細胞值和記憶細胞候選值來共同決定和更新當前細胞狀態:
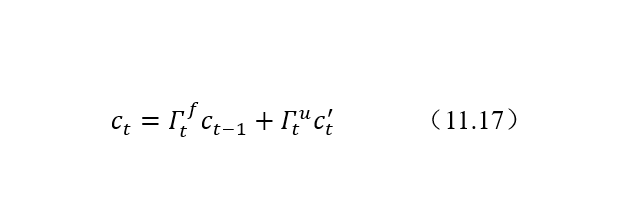
記憶細胞更新在LSTM整個結構中位置如圖8所示:
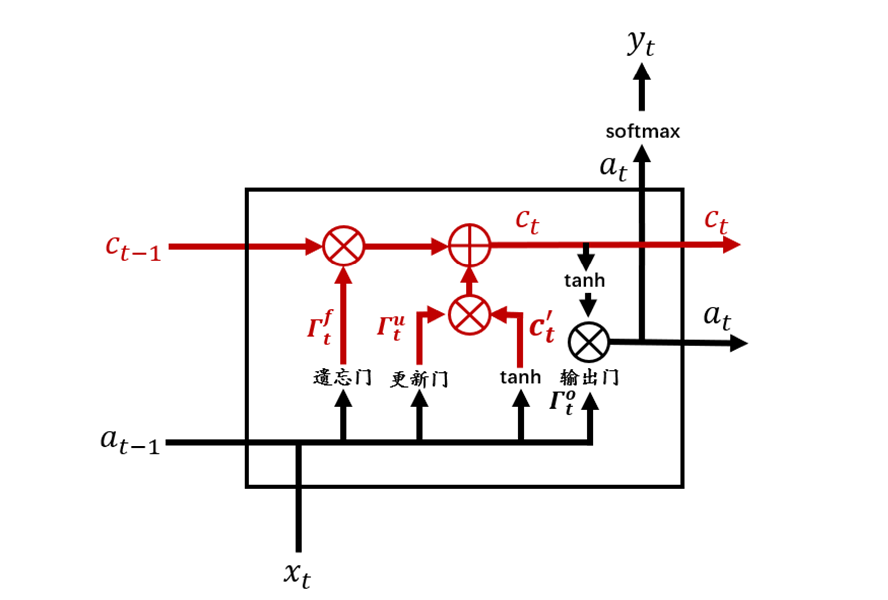
圖8 記憶細胞更新
5. 輸出門
LSTM 提供了單獨的輸出門(Output Gate)。計算公式如下:
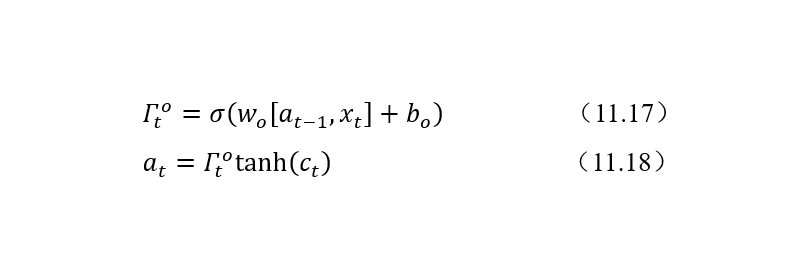
輸出門的位置如圖9所示。
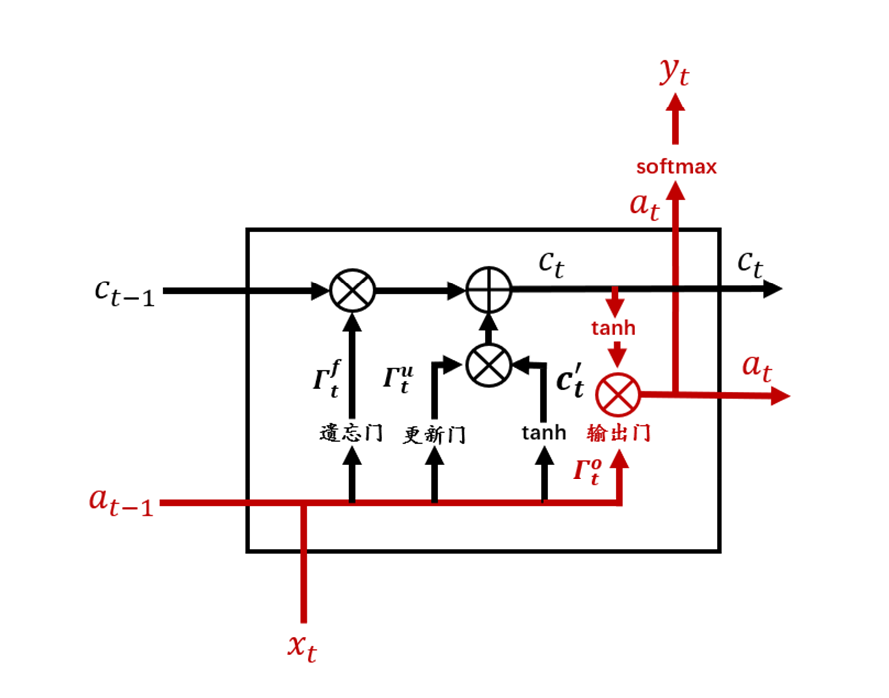
圖9 輸出門
以上便是完整的LSTM結構。雖然復雜,但經過逐步解析之后也就基本清晰了。LSTM 在自然語言處理、問答系統、股票預測等等領域都有著廣泛而深入的應用。
責任編輯:haq
-
神經網絡
+關注
關注
42文章
4774瀏覽量
100899 -
LSTM
+關注
關注
0文章
59瀏覽量
3767
原文標題:深入理解LSTM
文章出處:【微信號:sessdw,微信公眾號:三星半導體互動平臺】歡迎添加關注!文章轉載請注明出處。
發布評論請先 登錄
相關推薦




 深度神經網絡的困擾 梯度爆炸與梯度消失
深度神經網絡的困擾 梯度爆炸與梯度消失











評論