介紹
高效的管道設(shè)計(jì)對(duì)數(shù)據(jù)科學(xué)家至關(guān)重要。在編寫(xiě)復(fù)雜的端到端工作流時(shí),您可以從各種構(gòu)建塊中進(jìn)行選擇,每種構(gòu)建塊都專門(mén)用于特定任務(wù)。不幸的是,在數(shù)據(jù)格式之間重復(fù)轉(zhuǎn)換容易出錯(cuò),而且會(huì)降低性能。讓我們改變這一點(diǎn)!
在本系列博客中,我們將討論高效框架互操作性的不同方面:
在第一個(gè)職位中,我們討論了不同內(nèi)存布局以及異步內(nèi)存分配的內(nèi)存池的優(yōu)缺點(diǎn),以實(shí)現(xiàn)零拷貝功能。
在第二職位中,我們強(qiáng)調(diào)了數(shù)據(jù)加載/傳輸過(guò)程中出現(xiàn)的瓶頸,以及如何使用遠(yuǎn)程直接內(nèi)存訪問(wèn)( RDMA )技術(shù)緩解這些瓶頸。
在本文中,我們將深入討論端到端管道的實(shí)現(xiàn),展示所討論的跨數(shù)據(jù)科學(xué)框架的最佳數(shù)據(jù)傳輸技術(shù)。
要了解有關(guān)框架互操作性的更多信息,請(qǐng)查看我們?cè)?NVIDIA 的 GTC 2021 年會(huì)議上的演示。
讓我們深入了解以下方面的全功能管道的實(shí)現(xiàn)細(xì)節(jié):
從普通 CSV 文件解析 20 小時(shí)連續(xù)測(cè)量的電子 CTR 心電圖( ECG )。
使用傳統(tǒng)信號(hào)處理技術(shù)將定制 ECG 流無(wú)監(jiān)督分割為單個(gè)心跳。
用于異常檢測(cè)的變分自動(dòng)編碼器( VAE )的后續(xù)培訓(xùn)。
結(jié)果的最終可視化。
對(duì)于前面的每個(gè)步驟,都使用了不同的數(shù)據(jù)科學(xué)庫(kù),因此高效的數(shù)據(jù)轉(zhuǎn)換是一項(xiàng)至關(guān)重要的任務(wù)。最重要的是,在將數(shù)據(jù)從一個(gè)基于 GPU 的框架復(fù)制到另一個(gè)框架時(shí),應(yīng)該避免昂貴的 CPU 往返。
零拷貝操作:端到端管道
說(shuō)夠了!讓我們看看框架的互操作性。在下面,我們將逐步討論端到端管道。如果你是一個(gè)不耐煩的人,你可以直接在這里下載完整的 Jupyter 筆記本。源代碼可以在最近的RAPIDS docker 容器中執(zhí)行。
Getting started
In order to make it easier to have all those libraries up and running, we have used the RAPIDS 0.19 container on Ubuntu 18.04 as a base container, and then added a few missing libraries viapip install.
We encourage you to run this notebook on the latest RAPIDS container. Alternatively, you can also set up aconda virtual environment. In both cases, please visitRAPIDS release selectorfor installation details.
Finally, please find below the details of the container we used when creating this notebook . For reproducibility purposes, please use the following command:
foo@bar:~$ docker pull rapidsai/rapidsai-dev:21.06-cuda11.0-devel-ubuntu18.04-py3.7
foo@bar:~$ docker run --gpus all --rm -it -p 8888:8888 -p 8787:8787 -p 8786:8786 \
-v ~:/rapids/notebooks/host rapidsai/rapidsai-dev:21.06-cuda11.0-devel-ubuntu18.04-py3.7
步驟 1 :數(shù)據(jù)加載
在第一步中,我們下載 20 小時(shí)的 ele CTR 心電圖作為 CSV 文件,并將其寫(xiě)入磁盤(pán)(見(jiàn)單元格 1 )。之后,我們解析 CSV 文件中的 500 MB 標(biāo)量值,并使用 RAPIDS “ blazing fast CSV reader ”(參見(jiàn)單元格 2 )將其直接傳輸?shù)?GPU 。現(xiàn)在,數(shù)據(jù)駐留在 GPU 上,并將一直保留到最后。接下來(lái),我們使用cuxfilter( ku 交叉濾波器)框架繪制由 2000 萬(wàn)個(gè)標(biāo)量數(shù)據(jù)點(diǎn)組成的整個(gè)時(shí)間序列(見(jiàn)單元格 3 )。
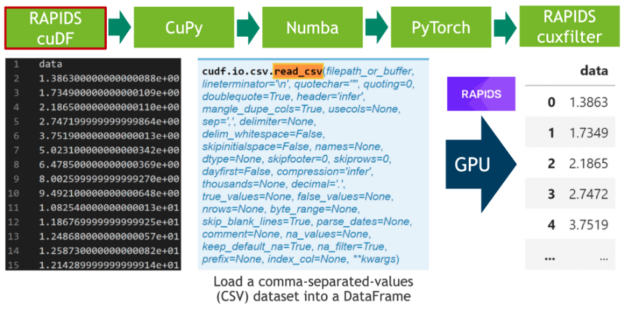
圖 1 :使用 RAPIDS CSV 解析器解析逗號(hào)分隔值( CSV )。
def retrieve_as_csv(url, root="./data"):
# local import because we will never see them again ;)
import os
import urllib
import zipfile
import numpy as np
from scipy.io import loadmat
filename = os.path.join(root, 'ECG_one_day.zip')
if not os.path.isdir(root):
os.makedirs(root)
if not os.path.isfile(filename):
urllib.request.urlretrieve(url, filename)
with zipfile.ZipFile(filename, 'r') as zip_ref:
zip_ref.extractall(root)
stream = loadmat(os.path.join(root, 'ECG_one_day','ECG.mat'))['ECG'].flatten()
csvname = os.path.join(root, 'heartbeats.csv')
if not os.path.isfile(csvname):
np.savetxt(csvname, stream[:-140000], delimiter=",", header="heartbeats", comments="")
# store the data as csv on disk
url = "https://www.cs.ucr.edu/~eamonn/ECG_one_day.zip"
retrieve_as_csv(url)
import cudf
heartbeats_cudf = cudf.read_csv("data/heartbeats.csv", dtype='float32')
heartbeats_cudf
| heartbeats | |
|---|---|
| 0 | -0.020 |
| 1 | -0.010 |
| 2 | -0.005 |
| 3 | -0.005 |
| 4 | -0.005 |
| ... | ... |
| 19999995 | -0.005 |
| 19999996 | 0.015 |
| 19999997 | 0.005 |
| 19999998 | -0.005 |
| 19999999 | 0.000 |
20000000 rows × 1 columns
Next, we will create a chart from theheartbeats_cudfDataFrame by making use of RAPIDScuxfilterlibrary.
We will get something similar to the following chart, but with a few nice features:
- The data is maintained in the GPU memory and operations like groupby aggregations, sorting and querying are done on the GPU itself, only returning the result as the output to the charts.
- The output is an interactive chart, facilitating data exploration.
import cuxfilter as cux
from cuxfilter.charts.datashader import line
# Chart width and height
WIDTH=600
HEIGHT=300
# 20 hours ECG look like a mess
heartbeats_cudf['x'] = heartbeats_cudf.index
line_cux = line(x='x', y='heartbeats', add_interaction=False)
_ = cux.DataFrame.from_dataframe(heartbeats_cudf).dashboard([line_cux])
line_cux.chart.title.text = 'ECG stream'
line_cux.chart.title.align = 'center'
line_cux.chart.width = WIDTH
line_cux.chart.height = HEIGHT
line_cux.view()[0]
步驟 2 :數(shù)據(jù)分割
在下一步中,我們使用傳統(tǒng)的信號(hào)處理技術(shù)將 20 小時(shí)的 ECG 分割成單個(gè)心跳。我們通過(guò)將 ECG 流與高斯分布的二階導(dǎo)數(shù)(也稱為里克爾小波)進(jìn)行卷積來(lái)實(shí)現(xiàn)這一點(diǎn),以便分離原型心跳中初始峰值的相應(yīng)頻帶。使用 CuPy (一種 CUDA 加速的密集線性代數(shù)和陣列運(yùn)算庫(kù))可以方便地進(jìn)行小波采樣和基于 FFT 的卷積運(yùn)算。直接結(jié)果是,存儲(chǔ) ECG 數(shù)據(jù)的 RAPIDS cuDF 數(shù)據(jù)幀必須使用 DLPack 作為零拷貝機(jī)制轉(zhuǎn)換為 CuPy 陣列。
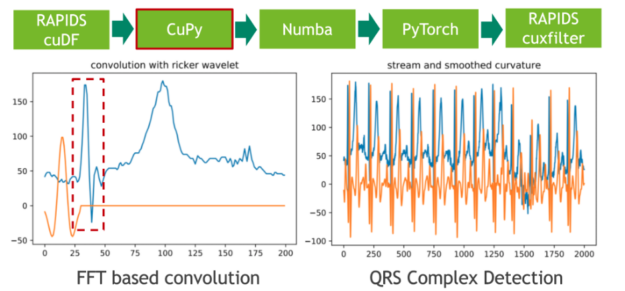
圖 2 :使用 CuPy 將 ele CTR 心圖( ECG )流與固定寬度的 Ricker 小波卷積。
卷積的特征響應(yīng)(結(jié)果)測(cè)量流中每個(gè)位置的固定頻率內(nèi)容的存在。請(qǐng)注意,我們選擇小波的方式使局部最大值對(duì)應(yīng)于心跳的初始峰值。
view rawCell040506.ipynb hosted with by GitHub
步驟 3 :局部極大值檢測(cè)
在下一步中,我們使用非最大抑制( NMS )的 1D 變體將這些極值點(diǎn)映射到二進(jìn)制門(mén)。 NMS 確定流中每個(gè)位置的對(duì)應(yīng)值是否為預(yù)定義窗口(鄰域)中的最大值。這個(gè)令人尷尬的并行問(wèn)題的 CUDA 實(shí)現(xiàn)非常簡(jiǎn)單。在我們的示例中,我們使用即時(shí)編譯器 Numba 實(shí)現(xiàn)無(wú)縫的 Python 集成。 Numba 和 Cupy 都將 CUDA 陣列接口實(shí)現(xiàn)為零拷貝機(jī)制,因此可以完全避免從 Cupy 陣列到 Numba 設(shè)備陣列的顯式轉(zhuǎn)換。
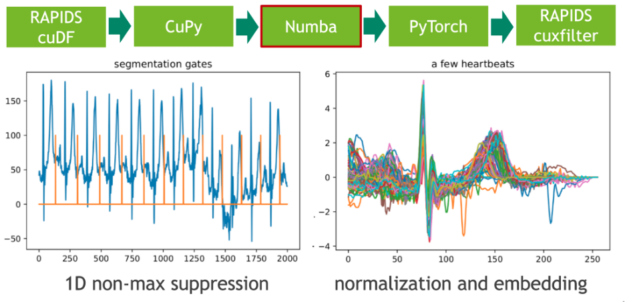
圖 3 :使用 Numba JIT 的 1D 非最大抑制和嵌入心跳。
每個(gè)心跳的長(zhǎng)度是通過(guò)計(jì)算門(mén)位置的相鄰差分(有限階導(dǎo)數(shù))來(lái)確定的。我們通過(guò)使用謂詞門(mén)== 1 過(guò)濾索引域,然后調(diào)用 cupy 。 diff ()來(lái)實(shí)現(xiàn)這一點(diǎn)。得到的直方圖描述了長(zhǎng)度分布。
Inspecting heart beat lengths
The binary mask gate_cupy is 1 for each position that starts a heartbeat and 0 otherwise. Subsequently, we want to transform this dense representation with many zeroes to a sparse one where one only stores the indices in the stream that start a heartbeat. You could write a CUDA-kernel usingwarp-aggregated atomicsfor that purpose. In CuPy, however, this can be achieved easier by filtering the index domain with the predicate gate==1. An adjacent difference (discrete derivative cupy.diff) computes the heartbeat lengths as index distance between positive gate positions. Finally, the computed lengths are visualized in a histogram.
def indices_and_lengths_cupy(gate):
# all indices 0 1 2 3 4 5 6 ...
iota = cp.arange(len(gate))
# after filtering with gate==1 it becomes 3 6 10
indices = iota[gate == 1]
lengths = cp.diff(indices)
return indices, lengths
from cuxfilter.charts import bar
# inspect the segment lengths, we will later prune very long and short segments
indices_cupy, lengths_cupy = indices_and_lengths_cupy(gate_cupy)
# currently, cuxfilter doesn't support histogram chart with density=True,
# so we will create a histogram chart from a bar chart
BINS=30
lengths_hist_cupy = cp.histogram(lengths_cupy, bins=BINS, density=True)
hist_range = cp.max(lengths_cupy) - cp.min(lengths_cupy)
hist_width = int(hist_range/BINS)
lengths_cudf = cudf.DataFrame({'length': lengths_hist_cupy[0]})
lengths_cudf = lengths_cudf.loc[lengths_cudf.index.repeat(hist_width)]
lengths_cudf['x'] = cp.arange(0, BINS * hist_width) + cp.min(lengths_cupy)
bar_cux = bar(x='x', y='length', add_interaction=False)
_ = cux.DataFrame.from_dataframe(lengths_cudf).dashboard([bar_cux])
bar_cux.chart.title.text = 'Segment lengths'
bar_cux.chart.title.align = 'center'
bar_cux.chart.left[0].axis_label = ""
bar_cux.chart.width = WIDTH
bar_cux.chart.height = HEIGHT
bar_cux.view()[0]
步驟 4 :候選修剪和嵌入
我們打算使用固定長(zhǎng)度的輸入矩陣在心跳集上訓(xùn)練(卷積)變分自動(dòng)編碼器( VAE )。用 CUDA 內(nèi)核可以實(shí)現(xiàn)心跳信號(hào)在零向量中的嵌入。在這里,我們?cè)俅问褂?Numba 進(jìn)行候選修剪和嵌入。
Candidate pruning and embedding in fixed length vectors
In a later stage we intend to train a Variational Autoencoder (VAE) with fixed-length input and thus the heartbeats must be embedded in a data matrix of fixed shape. According to the histogram the majority of length is somewhere in the range between 100 and 250. The embedding is accomplished with Numba kernel. A warp of 32 consecutive threads works on each heartbeat. The first thread in a warp (leader) checks if the heartbeat exhibits a valid length and increments a row counter in an atomic manner to determine the output row in the data matrix. Subsequently, the target row is communicated to the remaining 31 threads in the warp using the warp-intrinsic shfl_sync (broadcast). In a final step, we (re-)use the threads in the warp to write the values to the output row in the data matrix in a warp-cyclic fashion (warp-stride loop). Finally, we plot a few of the zero-embedded heartbeats and observe approximate alignment of the QRS complex -- exactly what we wanted to achieve.
@cuda.jit
def zero_padding_kernel(signal, indices, counter, lower, upper, out):
"""using warp intrinsics to speedup the calcuation"""
for candidate in range(cuda.blockIdx.x, indices.shape[0]-1, cuda.gridDim.x):
length = indices[candidate+1]-indices[candidate]
# warp-centric: 32 threads process one signal
if lower <= length <= upper:
entry = 0
if cuda.threadIdx.x == 0:
# here we select in thread 0 what will be the target row
entry = cuda.atomic.add(counter, 0, 1)
# broadcast the target row to all other threads
# all 32 threads (warp) know the value
entry = cuda.shfl_sync(0xFFFFFFFF, entry, 0)
for index in range(cuda.threadIdx.x, upper, 32):
out[entry, index] = signal[indices[candidate]+index] if index < length else 0.0
def zero_padding_numba(signal, indices, lengths, lower=100, upper=256):
mask = (lower <= lengths) * (lengths <= upper)
num_entries = int(cp.sum(mask))
out = cp.empty((num_entries, upper), dtype=signal.dtype)
counter = cp.zeros(1).astype(cp.int64)
zero_padding_kernel[80*32, 32](signal, indices, counter, lower, upper, out)
cuda.synchronize()
print("removed", 100-100*num_entries/len(lengths), "percent of the candidates")
return out
# let's prune the short and long segments (heartbeats) and normalize them
data_cupy = zero_padding_numba(heartbeats_cupy, indices_cupy, lengths_cupy, lower=100, upper=256)
removed 3.3824004429883274 percent of the candidates
# looks good, they are approximately aligned
HEARTBEATS_SAMPLE = 10
data_cudf = cudf.DataFrame({'y_{}'.format(i):data_cupy[i] for i in range(HEARTBEATS_SAMPLE)})
data_cudf['x'] = cp.arange(0, data_cupy.shape[1])
data_cudf = data_cudf.astype('float64')
stacked_lines_cux = stacked_lines(x='x', y=['y_{}'.format(i) for i in range(HEARTBEATS_SAMPLE)],
legend=False, add_interaction=False,
colors = ["red", "grey", "black", "purple", "pink",
"yellow", "brown", "green", "orange", "blue"])
_ = cux.DataFrame.from_dataframe(data_cudf).dashboard([stacked_lines_cux])
stacked_lines_cux.chart.title.text = 'A few heartbeats'
stacked_lines_cux.chart.title.align = 'center'
stacked_lines_cux.chart.width = WIDTH
stacked_lines_cux.chart.height = HEIGHT
stacked_lines_cux.view()[0]
步驟 5 :異常值檢測(cè)
在這一步中,我們?cè)?75% 的數(shù)據(jù)上訓(xùn)練 VAE 模型。 DLPack 再次用作零拷貝機(jī)制,將 CuPy 數(shù)據(jù)矩陣映射到 PyTorch 張量。
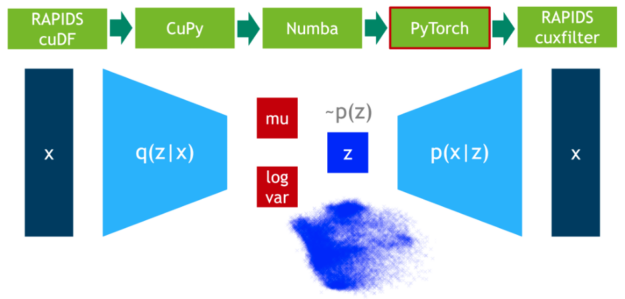
圖 4 :使用 PyTorch 訓(xùn)練可變自動(dòng)編碼器。
Installing PyTorch...
WARNING: Running pip as root will break packages and permissions. You should install packages reliably by using venv: https://pip.pypa.io/warnings/venv
Subsequently, we define the network topology. Here, we use a convolutional version but you could also experiment with a classicalMLP VAE.
import torch
class Swish(torch.nn.Module):
def __init__(self):
super().__init__()
self.alpha = torch.nn.Parameter(torch.tensor([1.0], requires_grad=True))
def forward(self, x):
return x*torch.sigmoid(self.alpha.to(x.device)*x)
class Downsample1d(torch.nn.Module):
def __init__(self):
super().__init__()
self.filter = torch.tensor([1.0, 2.0, 1.0]).view(1, 1, 3)
def forward(self, x):
w = torch.cat([self.filter]*x.shape[1], dim=0).to(x.device)
return torch.nn.functional.conv1d(x, w, stride=2, padding=1, groups=x.shape[1])
class LightVAE(torch.nn.Module):
def __init__(self, num_dims):
super(LightVAE, self).__init__()
self.num_dims = num_dims
assert num_dims & num_dims-1 == 0, "num_dims must be power of 2"
self.down = Downsample1d()
self.up = torch.nn.Upsample(scale_factor=2)
self.sigma = Swish()
self.conv0 = torch.nn.Conv1d(1, 2, kernel_size=3, stride=1, padding=1)
self.conv1 = torch.nn.Conv1d(2, 4, kernel_size=3, stride=1, padding=1)
self.conv2 = torch.nn.Conv1d(4, 8, kernel_size=3, stride=1, padding=1)
self.convA = torch.nn.Conv1d(8, 2, kernel_size=3, stride=1, padding=1)
self.convB = torch.nn.Conv1d(8, 2, kernel_size=3, stride=1, padding=1)
self.restore = torch.nn.Linear(2, 8*num_dims//8)
self.conv3 = torch.nn.Conv1d( 8, 4, kernel_size=3, stride=1, padding=1)
self.conv4 = torch.nn.Conv1d( 4, 2, kernel_size=3, stride=1, padding=1)
self.conv5 = torch.nn.Conv1d( 2, 1, kernel_size=3, stride=1, padding=1)
def encode(self, x):
x = x.view(-1, 1, self.num_dims)
x = self.down(self.sigma(self.conv0(x)))
x = self.down(self.sigma(self.conv1(x)))
x = self.down(self.sigma(self.conv2(x)))
return torch.mean(self.convA(x), dim=(2,)), \
torch.mean(self.convB(x), dim=(2,))
def reparameterize(self, mu, logvar):
std = torch.exp(0.5*logvar)
eps = torch.randn_like(std)
return mu + eps*std
def decode(self, z):
x = self.restore(z).view(-1, 8, self.num_dims//8)
x = self.sigma(self.conv3(self.up(x)))
x = self.sigma(self.conv4(self.up(x)))
return self.conv5(self.up(x)).view(-1, self.num_dims)
def forward(self, x):
mu, logvar = self.encode(x)
z = self.reparameterize(mu, logvar)
return self.decode(z), mu, logvar
# Reconstruction + KL divergence losses summed over all elements and batch
def loss_function(recon_x, x, mu, logvar):
MSE = torch.sum(torch.mean(torch.square(recon_x-x), dim=1))
# see Appendix B from VAE paper:
# Kingma and Welling. Auto-Encoding Variational Bayes. ICLR, 2014
# https://arxiv.org/abs/1312.6114
# 0.5 * sum(1 + log(sigma^2) - mu^2 - sigma^2)
KLD = -0.1 * torch.sum(torch.mean(1 + logvar - mu.pow(2) - logvar.exp(), dim=1))
return MSE + KLD
Pytorch expects its dedicated tensor type and thus we need to map the CuPy array data_cupy to a FloatTensor. We perform that again using zero-copy functionality via DLPack. The remaining code is plain Pytorch program that trains the VAE on the training set for 10 epochs using the Adam optimizer.
# zero-copy to pytorch tensors using dlpack
from torch.utils import dlpack
cp.random.seed(42)
cp.random.shuffle(data_cupy)
split = int(0.75*len(data_cupy))
trn_torch = dlpack.from_dlpack(data_cupy[:split].toDlpack())
tst_torch = dlpack.from_dlpack(data_cupy[split:].toDlpack())
dim = trn_torch.shape[1]
model = LightVAE(dim).to('cuda')
optimizer = torch.optim.Adam(model.parameters())
# let's train a VAE
NUM_EPOCHS = 10
BATCH_SIZE = 1024
trn_loader = torch.utils.data.DataLoader(trn_torch, batch_size=BATCH_SIZE, shuffle=True)
tst_loader = torch.utils.data.DataLoader(tst_torch, batch_size=BATCH_SIZE, shuffle=False)
model.train()
for epoch in range(NUM_EPOCHS):
trn_loss = 0.0
for data in trn_loader:
optimizer.zero_grad()
recon_batch, mu, logvar = model(data)
loss = loss_function(recon_batch, data, mu, logvar)
loss.backward()
trn_loss += loss.item()
optimizer.step()
print('====> Epoch: {} Average loss: {:.4f}'.format(
epoch, trn_loss / len(trn_loader.dataset)))
====> Epoch: 0 Average loss: 0.0186 ====> Epoch: 1 Average loss: 0.0077 ====> Epoch: 2 Average loss: 0.0066 ====> Epoch: 3 Average loss: 0.0063 ====> Epoch: 4 Average loss: 0.0061 ====> Epoch: 5 Average loss: 0.0060 ====> Epoch: 6 Average loss: 0.0059 ====> Epoch: 7 Average loss: 0.0059 ====> Epoch: 8 Average loss: 0.0058 ====> Epoch: 9 Average loss: 0.0058
步驟 6 :結(jié)果可視化
在最后一步中,我們可視化剩余 25% 數(shù)據(jù)的潛在空間。
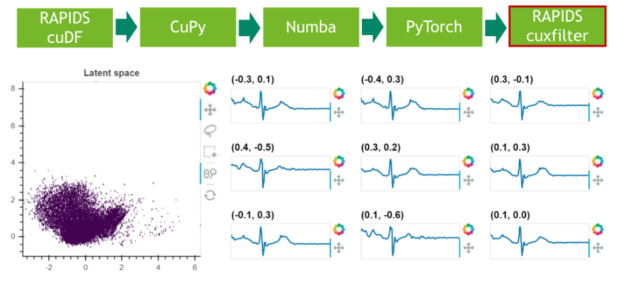
圖 5 :使用 RAPIDS cuxfilter 對(duì)潛在空間進(jìn)行采樣和可視化。
Let's check if the test loss is in the same range:
# it will be used to visualize a scatter char
mu_cudf = cudf.DataFrame()
model.eval()
with torch.no_grad():
tst_loss = 0
for data in tst_loader:
recon_batch, mu, logvar = model(data)
tst_loss += loss_function(recon_batch, data, mu, logvar).item()
mu_cudf = mu_cudf.append(cudf.DataFrame(mu, columns=['x', 'y']))
tst_loss /= len(tst_loader.dataset)
print('====> Test set loss: {:.4f}'.format(tst_loss))
====> Test set loss: 0.0074
Finally, we visualize the latent space which is an approximate isotropic Gaussian centered around the origin:
from cuxfilter.charts import scatter
scatter_chart_cux = scatter(x='x', y='y', pixel_shade_type="linear",
legend=False, add_interaction=False)
_ = cux.DataFrame.from_dataframe(mu_cudf).dashboard([scatter_chart_cux])
scatter_chart_cux.chart.title.text = 'Latent space'
scatter_chart_cux.chart.title.align = 'center'
scatter_chart_cux.chart.width = WIDTH
scatter_chart_cux.chart.height = 2*HEIGHT
scatter_chart_cux.view()[0]
結(jié)論
從這篇和前面的博文中可以看出,互操作性對(duì)于設(shè)計(jì)高效的數(shù)據(jù)管道至關(guān)重要。在不同的框架之間復(fù)制和轉(zhuǎn)換數(shù)據(jù)是一項(xiàng)昂貴且極其耗時(shí)的任務(wù),它為數(shù)據(jù)科學(xué)管道增加了零價(jià)值。數(shù)據(jù)科學(xué)工作負(fù)載變得越來(lái)越復(fù)雜,多個(gè)軟件庫(kù)之間的交互是常見(jiàn)的做法。 DLPack 和 CUDA 陣列接口是事實(shí)上的數(shù)據(jù)格式標(biāo)準(zhǔn),保證了基于 GPU 的框架之間的零拷貝數(shù)據(jù)交換。
對(duì)外部?jī)?nèi)存管理器的支持是一個(gè)很好的特點(diǎn),在評(píng)估您的管道將使用哪些軟件庫(kù)時(shí)要考慮。例如,如果您的任務(wù)同時(shí)需要數(shù)據(jù)幀和數(shù)組數(shù)據(jù)操作,那么最好選擇 RAPIDS cuDF + CuPy 庫(kù)。它們都受益于 GPU 加速,支持 DLPack 以零拷貝方式交換數(shù)據(jù),并共享同一個(gè)內(nèi)存管理器 RMM 。或者, RAPIDS cuDF + JAX 也是一個(gè)很好的選擇。然而,后一種組合 或許需要額外的開(kāi)發(fā)工作來(lái)利用內(nèi)存使用,因?yàn)?JAX 缺乏對(duì)外部?jī)?nèi)存分配器的支持。
在處理大型數(shù)據(jù)集時(shí),數(shù)據(jù)加載和數(shù)據(jù)傳輸瓶頸經(jīng)常出現(xiàn)。 NVIDIA GPU 直接技術(shù)起到了解救作用,它支持將數(shù)據(jù)移入或移出 GPU 內(nèi)存,而不會(huì)加重 CPU 的負(fù)擔(dān),并將不同節(jié)點(diǎn)上 GPU 之間傳輸數(shù)據(jù)時(shí)所需的數(shù)據(jù)副本數(shù)量減少到一個(gè)。
關(guān)于作者
Christian Hundt 在德國(guó)美因茨的 Johannes Gutenberg 大學(xué)( JGU )獲得了理論物理的文憑學(xué)位。在他的博士論文中,他研究了時(shí)間序列數(shù)據(jù)挖掘算法在大規(guī)模并行架構(gòu)上的并行化。作為并行和分布式體系結(jié)構(gòu)組的博士后研究員,他專注于各種生物醫(yī)學(xué)應(yīng)用的高效并行化,如上下文感知的元基因組分類、基因集富集分析和胸部 mri 的深層語(yǔ)義圖像分割。他目前的職位是深度學(xué)習(xí)解決方案架構(gòu)師,負(fù)責(zé)協(xié)調(diào)盧森堡的 NVIDIA 人工智能技術(shù)中心( NVAITC )的技術(shù)合作。
Miguel Martinez 是 NVIDIA 的高級(jí)深度學(xué)習(xí)數(shù)據(jù)科學(xué)家,他專注于 RAPIDS 和 Merlin 。此前,他曾指導(dǎo)過(guò) Udacity 人工智能納米學(xué)位的學(xué)生。他有很強(qiáng)的金融服務(wù)背景,主要專注于支付和渠道。作為一個(gè)持續(xù)而堅(jiān)定的學(xué)習(xí)者, Miguel 總是在迎接新的挑戰(zhàn)。
審核編輯:郭婷
-
編碼器
+關(guān)注
關(guān)注
45文章
3651瀏覽量
134827 -
NVIDIA
+關(guān)注
關(guān)注
14文章
5038瀏覽量
103305 -
gpu
+關(guān)注
關(guān)注
28文章
4754瀏覽量
129099
發(fā)布評(píng)論請(qǐng)先 登錄
相關(guān)推薦
智能網(wǎng)聯(lián)汽車云控系統(tǒng)第2部分:車云數(shù)據(jù)交互規(guī)范
優(yōu)化多相穩(wěn)壓器的高端FET電壓振鈴(第2部分)

如何進(jìn)行電源設(shè)計(jì)–第2部分

如何進(jìn)行電源設(shè)計(jì)–第3部分

電源設(shè)計(jì)方法-第5部分

電源設(shè)計(jì)方法-第6部分

電源設(shè)計(jì)方法-第3部分

電源設(shè)計(jì)方法-第2部分

電源設(shè)計(jì)方法-第1部分

電源設(shè)計(jì)方法-第4部分

如何進(jìn)行電源供應(yīng)設(shè)計(jì)-第3部分

互操作性對(duì)智能家居的重要性

是德科技攜手高通突破5G高頻段FR3互操作性
詳解TSMaster CAN 與 CANFD 的 CRC E2E 校驗(yàn)方法





 高效框架互操作性第3部分:使用E2E管道實(shí)現(xiàn)零拷貝
高效框架互操作性第3部分:使用E2E管道實(shí)現(xiàn)零拷貝










評(píng)論