經常拿回溯算法來說事兒的,無非就是八皇后問題和數獨問題了。那我們今天就通過實際且有趣的例子來講一下如何用回溯算法來解決數獨問題。
一、直觀感受
說實話我小的時候也嘗試過玩數獨游戲,但從來都沒有完成過一次。做數獨是有技巧的,我記得一些比較專業的數獨游戲軟件,他們會教你玩數獨的技巧,不過在我看來這些技巧都太復雜,我根本就沒有興趣看下去。
不過自從我學習了算法,多困難的數獨問題都攔不住我了。下面是我用程序完成數獨的一個例子:

PS:GIF 可能出現 bug,若卡住點開查看即可,下同。
這是一個安卓手機中的數獨游戲,我使用一個叫做 Auto.js 的腳本引擎,配合回溯算法來實現自動完成填寫,并且算法記錄了執行次數。
在后文,我會給出該腳本的實現思路代碼以及軟件工具的下載,你也可以拿來裝13用。
可以觀察到前兩次都執行了 1 萬多次,而最后一次只執行了 100 多次就算出了答案,這說明對于不同的局面,回溯算法得到答案的時間是不相同的。
那么計算機如何解決數獨問題呢?其實非常的簡單,就是窮舉嘛,下面我可視化了求解過程:
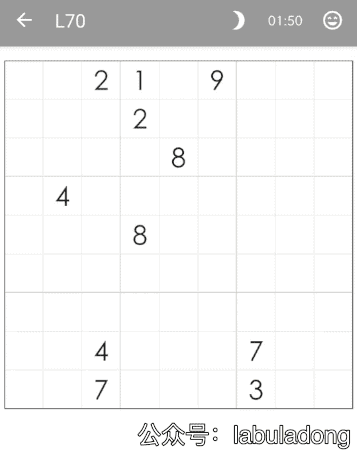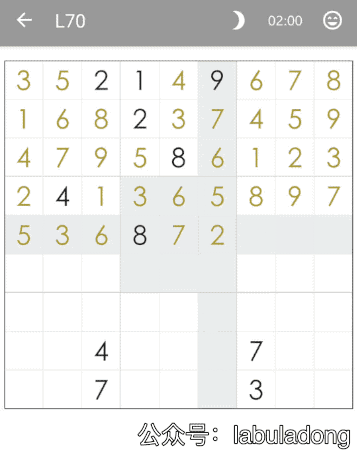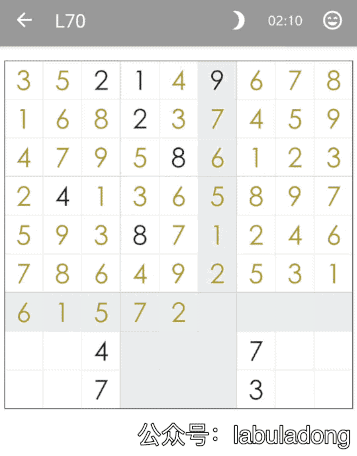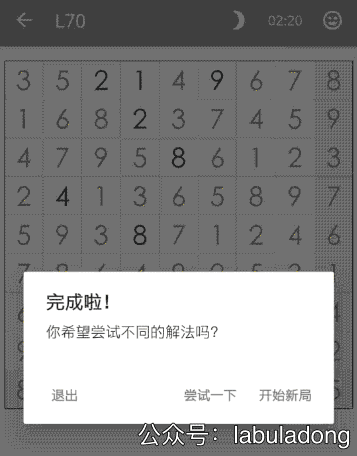
算法的核心思路非常非常的簡單,就是對每一個空著的格子窮舉 1 到 9,如果遇到不合法的數字(在同一行或同一列或同一個 3×3 的區域中存在相同的數字)則跳過,如果找到一個合法的數字,則繼續窮舉下一個空格子。
對于數獨游戲,也許我們還會有另一個誤區:就是下意識地認為如果給定的數字越少那么這個局面的難度就越大。
這個結論對人來說應該沒毛病,但對于計算機而言,給的數字越少,反而窮舉的步數就越少,得到答案的速度越快,至于為什么,我們后面探討代碼實現的時候會講。
上一個 GIF 是最后一關 70 關,下圖是第 52 關,數字比較多,看起來似乎不難,但是我們看一下算法執行的過程:
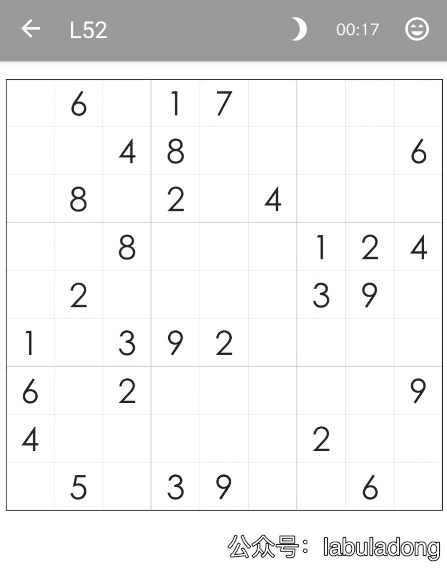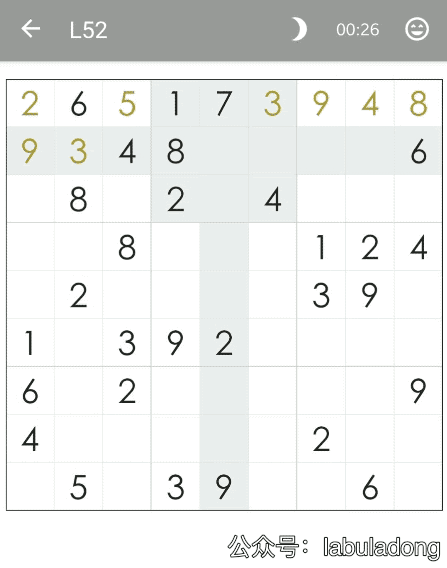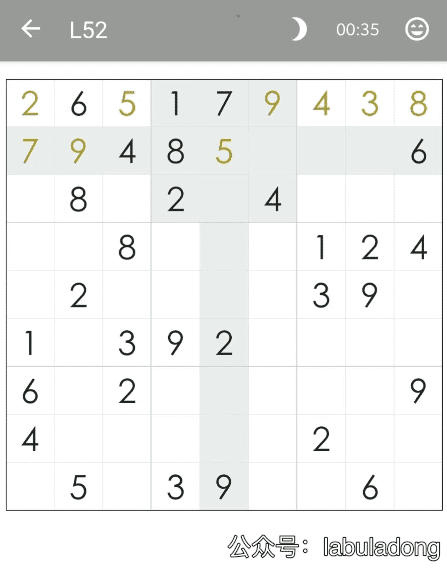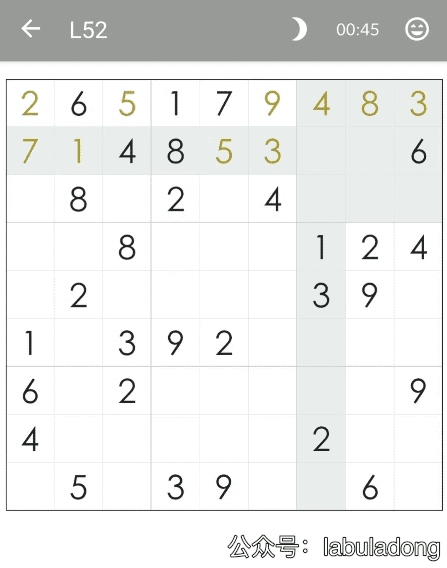
可以看到算法在前兩行窮舉了半天都沒有走出去,由于時間原因我就沒有繼續錄制了,事實上,這個局面窮舉的次數大概是上一個局面的 10 倍。
言歸正傳,下面我們就來具體探討一下如何用算法來求解數獨問題,順便說說我是如何可視化這個求解過程的。
二、代碼實現
首先,我們不用管游戲的 UI,先單純地解決回溯算法,LeetCode 第 37 題就是解數獨的問題,算法函數簽名如下:
voidsolveSudoku(char[][]board);
輸入是一個9x9的棋盤,空白格子用點號字符.表示,算法需要在原地修改棋盤,將空白格子填上數字,得到一個可行解。
至于數獨的要求,大家想必都很熟悉了,每行,每列以及每一個 3×3 的小方格都不能有相同的數字出現。那么,現在我們直接套回溯框架即可求解。
前文回溯算法詳解,已經寫過了回溯算法的套路框架,如果還沒看過那篇文章的,建議先看看。
回憶剛才的 GIF 圖片,我們求解數獨的思路很簡單粗暴,就是對每一個格子所有可能的數字進行窮舉。對于每個位置,應該如何窮舉,有幾個選擇呢?
很簡單啊,從 1 到 9 就是選擇,全部試一遍不就行了:
//對board[i][j]進行窮舉嘗試
voidbacktrack(char[][]board,inti,intj){
intm=9,n=9;
for(charch='1';ch<=?'9';ch++){
//做選擇
board[i][j]=ch;
//繼續窮舉下一個
backtrack(board,i,j+1);
//撤銷選擇
board[i][j]='.';
}
}
emmm,再繼續細化,并不是 1 到 9 都可以取到的,有的數字不是不滿足數獨的合法條件嗎?而且現在只是給j加一,那如果j加到最后一列了,怎么辦?
很簡單,當j到達超過每一行的最后一個索引時,轉為增加i開始窮舉下一行,并且在窮舉之前添加一個判斷,跳過不滿足條件的數字:
voidbacktrack(char[][]board,inti,intj){
intm=9,n=9;
if(j==n){
//窮舉到最后一列的話就換到下一行重新開始。
backtrack(board,i+1,0);
return;
}
//如果該位置是預設的數字,不用我們操心
if(board[i][j]!='.'){
backtrack(board,i,j+1);
return;
}
for(charch='1';ch<=?'9';ch++){
//如果遇到不合法的數字,就跳過
if(!isValid(board,i,j,ch))
continue;
board[i][j]=ch;
backtrack(board,i,j+1);
board[i][j]='.';
}
}
//判斷board[r][c]是否可以填入n
booleanisValid(char[][]board,intr,intc,charn){
for(inti=0;i9;i++){
//判斷行是否存在重復
if(board[r][i]==n)returnfalse;
//判斷列是否存在重復
if(board[i][c]==n)returnfalse;
//判斷3x3方框是否存在重復
if(board[(r/3)*3+i/3][(c/3)*3+i%3]==n)
returnfalse;
}
returntrue;
}
emmm,現在基本上差不多了,還剩最后一個問題:這個算法沒有 base case,永遠不會停止遞歸。這個好辦,什么時候結束遞歸?顯然r == m的時候就說明窮舉完了最后一行,完成了所有的窮舉,就是 base case。
另外,前文也提到過,為了減少復雜度,我們可以讓backtrack函數返回值為boolean,如果找到一個可行解就返回 true,這樣就可以阻止后續的遞歸。只找一個可行解,也是題目的本意。
最終代碼修改如下:
booleanbacktrack(char[][]board,inti,intj){
intm=9,n=9;
if(j==n){
//窮舉到最后一列的話就換到下一行重新開始。
returnbacktrack(board,i+1,0);
}
if(i==m){
//找到一個可行解,觸發basecase
returntrue;
}
if(board[i][j]!='.'){
//如果有預設數字,不用我們窮舉
returnbacktrack(board,i,j+1);
}
for(charch='1';ch<=?'9';ch++){
//如果遇到不合法的數字,就跳過
if(!isValid(board,i,j,ch))
continue;
board[i][j]=ch;
//如果找到一個可行解,立即結束
if(backtrack(board,i,j+1)){
returntrue;
}
board[i][j]='.';
}
//窮舉完1~9,依然沒有找到可行解,此路不通
returnfalse;
}
booleanisValid(char[][]board,intr,intc,charn){
//見上文
}
現在可以回答一下之前的問題,為什么有時候算法執行的次數多,有時候少?為什么對于計算機而言,確定的數字越少,反而算出答案的速度越快?
我們已經實現了一遍算法,掌握了其原理,回溯就是從 1 開始對每個格子窮舉,最后只要試出一個可行解,就會立即停止后續的遞歸窮舉。所以暴力試出答案的次數和隨機生成的棋盤關系很大,這個是說不準的。
那么你可能問,既然運行次數說不準,那么這個算法的時間復雜度是多少呢?
對于這種時間復雜度的計算,我們只能給出一個最壞情況,也就是 O(9^M),其中M是棋盤中空著的格子數量。你想嘛,對每個空格子窮舉 9 個數,結果就是指數級的。
這個復雜度非常高,但稍作思考就能發現,實際上我們并沒有真的對每個空格都窮舉 9 次,有的數字會跳過,有的數字根本就沒有窮舉,因為當我們找到一個可行解的時候就立即結束了,后續的遞歸都沒有展開。
這個 O(9^M) 的復雜度實際上是完全窮舉,或者說是找到所有可行解的時間復雜度。
如果給定的數字越少,相當于給出的約束條件越少,對于計算機這種窮舉策略來說,是更容易進行下去,而不容易走回頭路進行回溯的,所以說如果僅僅找出一個可行解,這種情況下窮舉的速度反而比較快。
至此,回溯算法就完成了,你可以用以上代碼通過 LeetCode 的判題系統,下面我們來簡單說下我是如何把這個回溯過程可視化出來的。
三、算法可視化
讓算法幫我玩游戲的核心是算法,如果你理解了這個算法,剩下就是借助安卓腳本引擎 Auto.js 調 API 操作手機了,工具我都放在后臺了,你等會兒就可以下載。
用偽碼簡單說下思路,我可以寫兩個函數:
voidsetNum(Buttonb,charn){
//輸入一個方格,將該方格設置為數字n
}
voidcancelNum(Buttonb){
//輸入一個方格,將該方格上的數字撤銷
}
回溯算法的核心框架如下,只要在框架對應的位置加上對應的操作,即可將算法做選擇、撤銷選擇的過程完全展示出來,也許這就是套路框架的魅力所在:
for(charch='1';ch<=?'9';ch++){
Buttonb=newButton(r,c);
//做選擇
setNum(b,ch);
board[i][j]=ch;
//繼續窮舉下一個
backtrack(board,i,j+1);
//撤銷選擇
cancelNum(b);
board[i][j]='.';
}
以上思路就可以模擬出算法窮舉的過程:

--- EOF ---
審核編輯 :李倩
-
代碼
+關注
關注
30文章
4815瀏覽量
68858 -
回溯算法
+關注
關注
0文章
10瀏覽量
6623
原文標題:搞懂回溯算法,我終于能做數獨了
文章出處:【微信號:TheAlgorithm,微信公眾號:算法與數據結構】歡迎添加關注!文章轉載請注明出處。
發布評論請先 登錄
相關推薦
Pure path studio內能否自己創建一個component,來實現特定的算法,例如LMS算法?
RVBacktrace RISC-V極簡棧回溯組件

回溯英特爾在跨越半個世紀的發展歷程
神經網絡如何用無監督算法訓練
bp神經網絡算法的基本流程包括哪些
工控主機的集顯和獨顯口怎么區分





 如何用回溯算法來解決數獨問題
如何用回溯算法來解決數獨問題











評論