訓練深度神經網絡是一項具有挑戰性的任務。多年來，研究人員提出了不同的方法來加速和穩定學習過程。歸一化是一種被證明在這方面非常有效的技術。

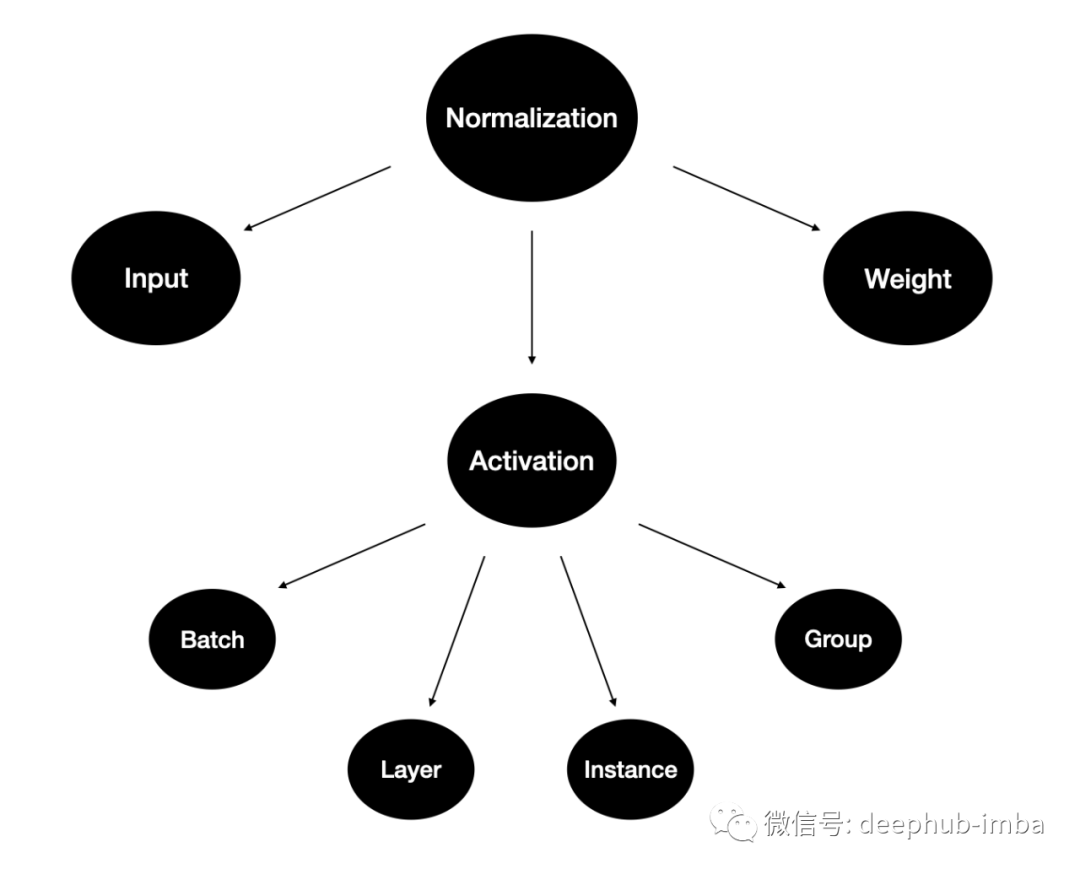
在這篇文章中，我將使用類比和可視化的方式來回顧這些方法中，這將幫助您了解它們的產生的原因和思維過程。

為什么要歸一化？

例如，我們現在用兩個特征構建一個簡單的神經網絡模型。這兩個特征一個是年齡：范圍在 0 到 65 之間，另一個是工資：范圍從 0 到 10 000。我們將這些特征提供給模型并計算梯度。

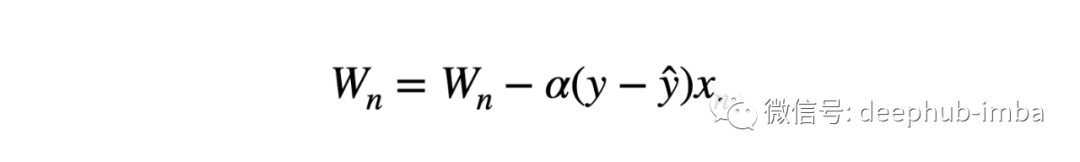
不同規模的輸入導致不同的權重更新和優化器的步驟向最小值的方向不均衡。這也使損失函數的形狀不成比例。在這種情況下，就需要使用較低的學習速率來避免過沖，這就意味著較慢的學習過程。

所以我們的解決方案是輸入進行歸一化，通過減去平均值(定心)并除以標準偏差來縮小特征。

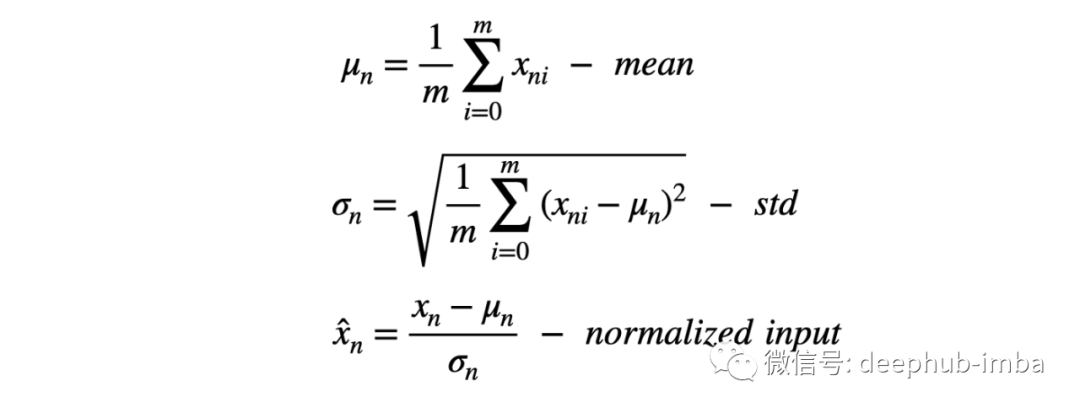
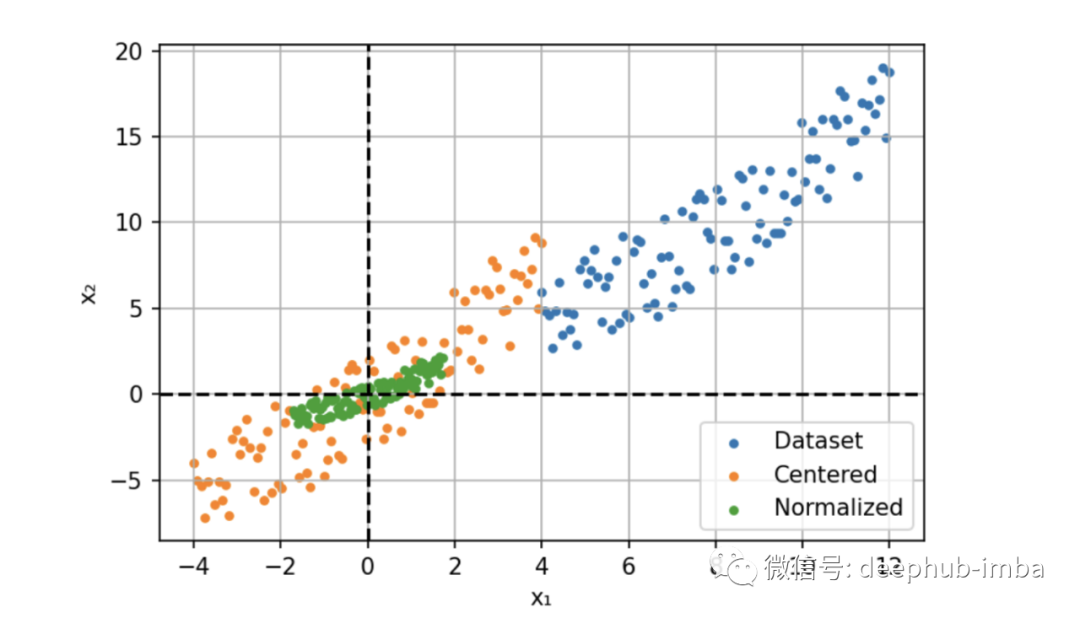
此過程也稱為“漂白”，處理后所有的值具有 0 均值和單位方差，這樣可以提供更快的收斂和更穩定的訓練。

這是一個很好的解決方案，那么為什么我們不規范化網絡中每一層的激活呢？

下面我們先看一下針對于激活的歸一化方法

Batch Normalization

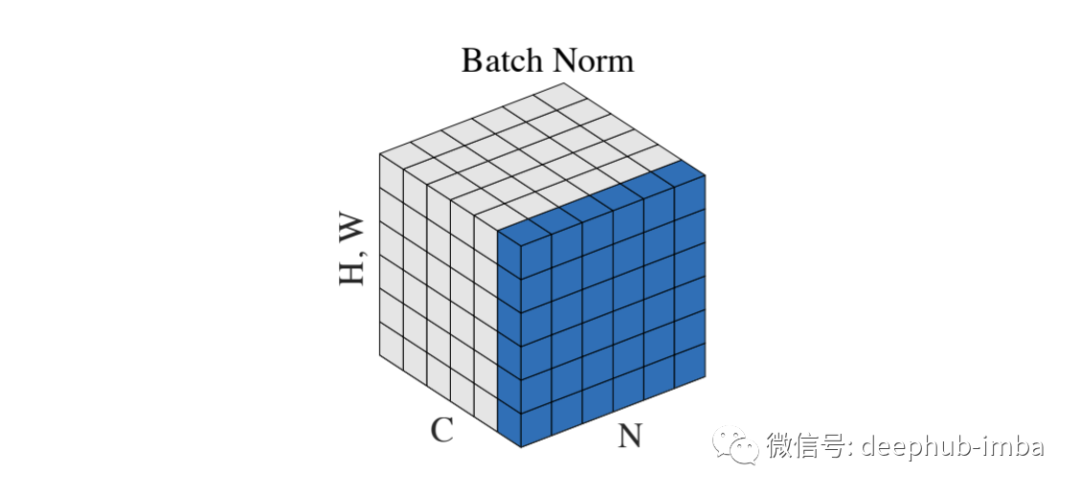
2015 年，Sergey Ioffe 和 Christian Szegedy[3] 采用了這個想法來解決內部協變量偏移問題。以前輸入層分布由于權值的更新而不斷變化。所以下面的層總是需要適應新的分布，它會導致收斂速度變慢和訓練不穩定。

批量標準化提供了一種控制和優化每一層之后的分布的方法。該過程與輸入歸一化相同，但我們添加了兩個可學習的參數，γ 和 β。

通過代碼來說明要比枯燥的公式好的多，所以BN的代碼如下：

def BatchNorm(x, gamma, beta, eps=1e-5): # x: input shape [N, C, H, W] N, C, H, W = x.shape mean = torch.mean(input=x, dim=[0,2,3], keepdim=True) var = torch.var(input=x, dim=[0,2,3], keepdim=True) # mean, var shape : [1, C, 1, 1] x = (x - mean) / torch.sqrt(var + eps) return x * gamma + beta

這兩個參數是通過反向傳播沿著網絡學習的。他們通過縮放(γ)和移動(β)激活優化分布。

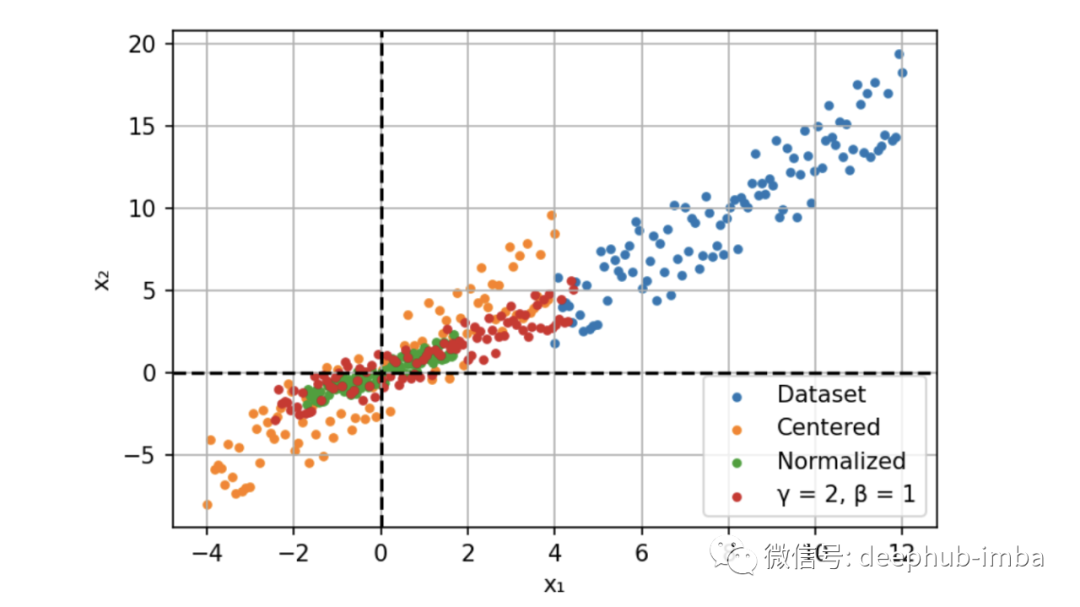
由于有固定的分布，所以可以提高學習率并加快收斂速度。除了計算提升之外，BN 還可以作為一種正則化技術。數據集統計數據的近似產生的噪聲消除了對 Dropout 的需要。

但這是一把雙刃劍。這種估計僅適用于較大的批次。當批次數量較少時，性能會急劇下降。

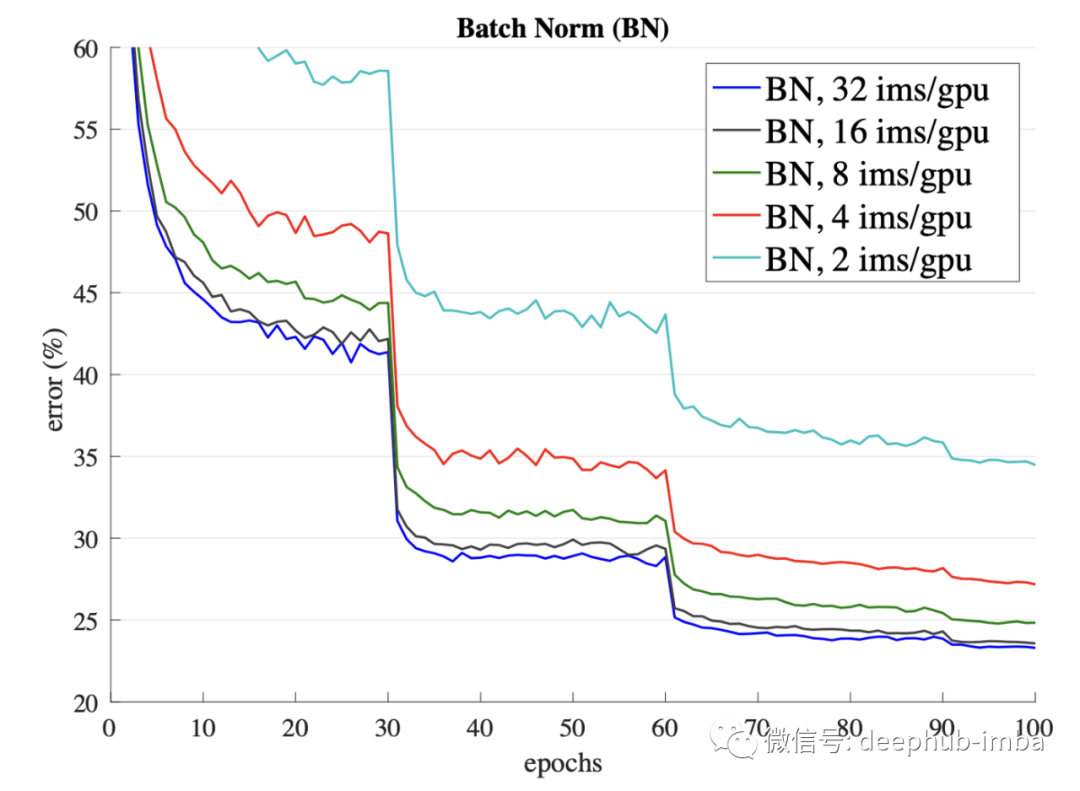
BN 的另一個缺點是對于批處理的依賴。如果我們傳遞了單個樣本而不是批量的樣本，網絡必須使用預先計算的訓練均值和方差，這可能會導致不同的結果。

這個問題的重要性促使人們創建替代方法以避免對批處理的依賴。

Layer Normalization

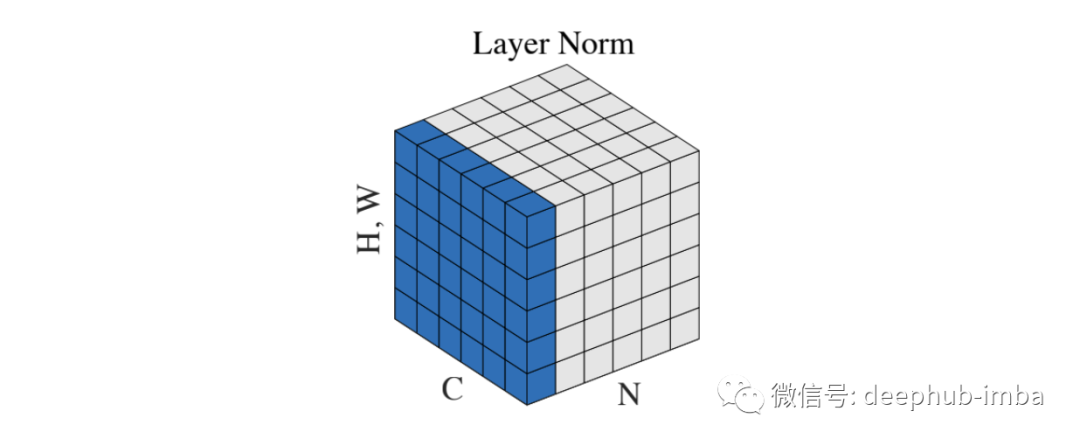
這是Geoffrey E. Hinton等人在2016年[4]中首次嘗試減少對批大小的約束。提出這個方法的主要原因是無法找到將BN應用于遞歸神經網絡，需要找到一個替代的方法。

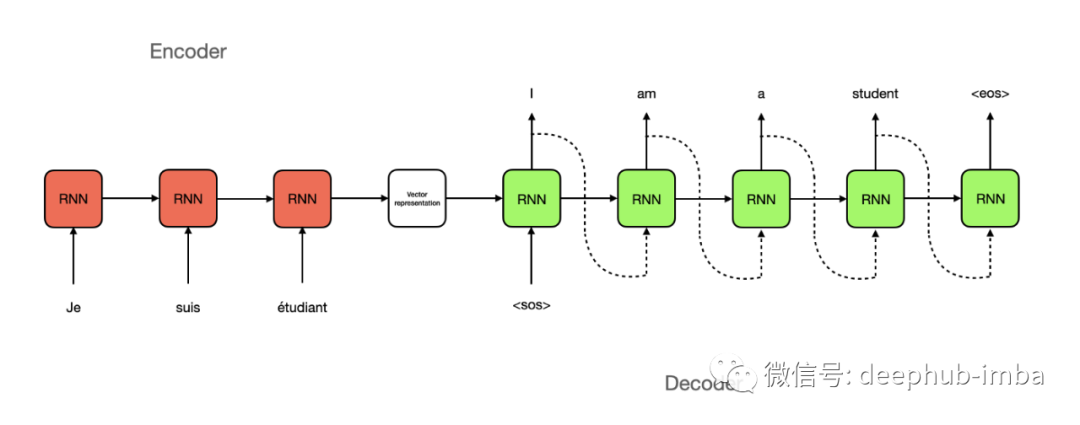
在深度神經網絡中，由于層數是固定的，因此很容易存儲每個 BN 層的統計信息。然而在 RNN 中，輸入和輸出形狀的長度不同。因此，在這種情況下，最好使用單個時間步長（樣本）而不是整個批次的統計信息進行標準化。

def LayerNorm(x, gamma, beta, eps=1e-5): # x: input shape [N, C, H, W] N, C, H, W = x.shape mean = torch.mean(input=x, dim=[1,2,3], keepdim=True) var = torch.var(input=x, dim=[1,2,3], keepdim=True) # mean, var shape: [N, 1, 1, 1] x = (x - mean) / torch.sqrt(var + eps) return x * gamma + beta

在這種方法中，batch(N) 中的每個示例都在 [C, H, W] 維度上進行了歸一化。與 BN 一樣，它可以加速和穩定訓練，并且不受批次的限制。此方法可用于批量為 1 的在線學習任務。

Instance Normalization

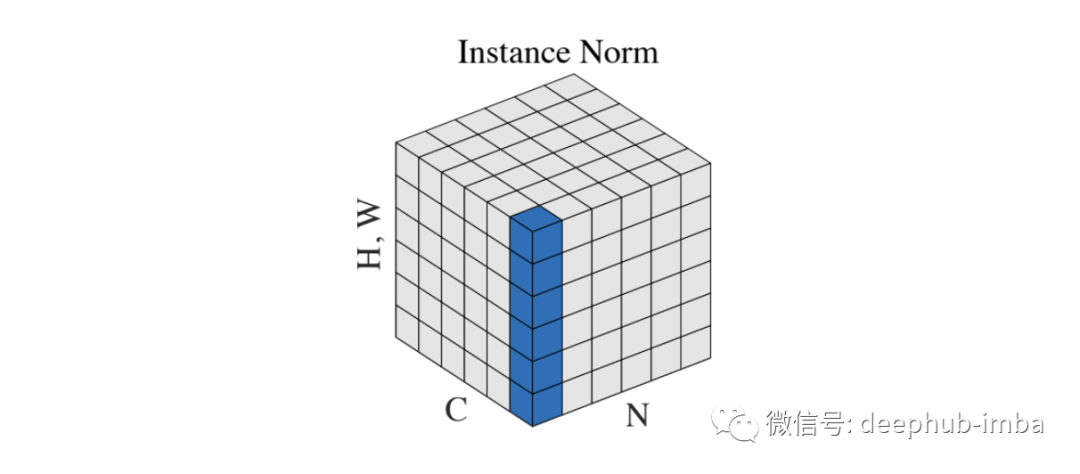
Dmitry Ulyanov 等人在 2016 年的論文 [5] 中介紹了Instance Normalization。這是另一種嘗試減少對批處理的依賴以改善樣式傳輸網絡的結果。

def InstanceNorm(x, gamma, beta, eps=1e-5): # x: input shape [N, C, H, W] N, C, H, W = x.shape mean = torch.mean(input=x, dim=[2,3], keepdim=True) var = torch.var(input=x, dim=[2,3], keepdim=True) # mean, var shape: [N, C, 1, 1] x = (x - mean) / torch.sqrt(var + eps) return x * gamma + beta

跨批次和通道的標準化允許從圖像中刪除特定的對比度信息，這有助于泛化。

這種方法在 Pix2Pix 或 CycleGAN 等生成模型中廣受歡迎，并成為著名的 StyleGAN2 中使用的自適應實例歸一化的先驅。

Group Normalization

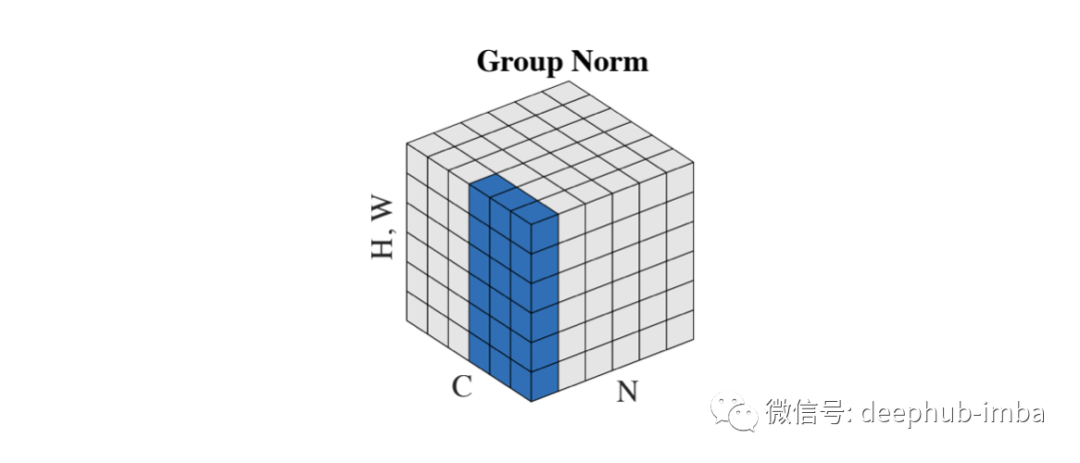
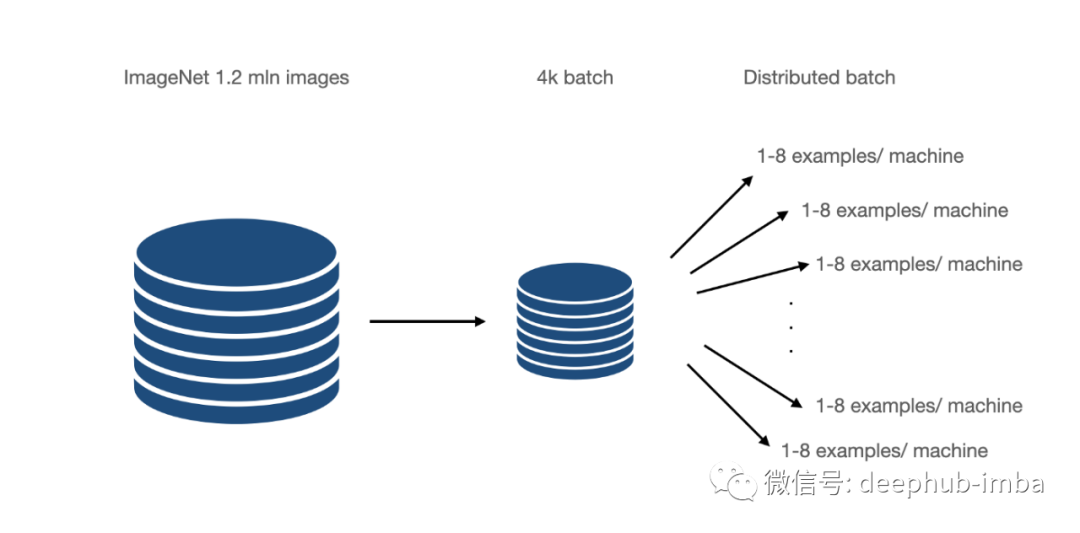
Group Normalization 在 2018[1] 論文中被引入，它直接解決了 CNN 的 BN 限制。主要針對的是分布式學習，其中批次被分成許多機器。這些是在少數例子上訓練的，比如 6-8，在某些情況下，甚至是 1-2。

GN 可以理解為Layer 和Instance的混合。GN 將通道分成組并在它們之間進行標準化。該方案使計算獨立于批量大小。

def GroupNorm(x, gamma, beta, G, eps=1e-5): # x: input features with shape [N, C, H, W] # G : number of groups N, C, H, W = x.shape x = torch.reshape(input=x, shape=[N, G, C // G, H, W]) mean = torch.mean(input=x, dim=[2,3,4], keepdim=True) var = torch.var(input=x, dim=[2,3,4], keepdim=True) # mean, var shape : [N, G, 1, 1, 1] x = (x - mean) / torch.sqrt(var + eps) x = torch.reshape(input=x, shape=[N, C, H, W]) return x * gamma + beta

GN 優于在小批量上訓練的 BN，但無法擊敗大批量的結果，但是這是一個很好的起點。

上面的針對于激活的歸一化方法我們基本上都聽說過也經常會用到，下面我們來介紹針對權重的歸一化方法。

Weight Standardization

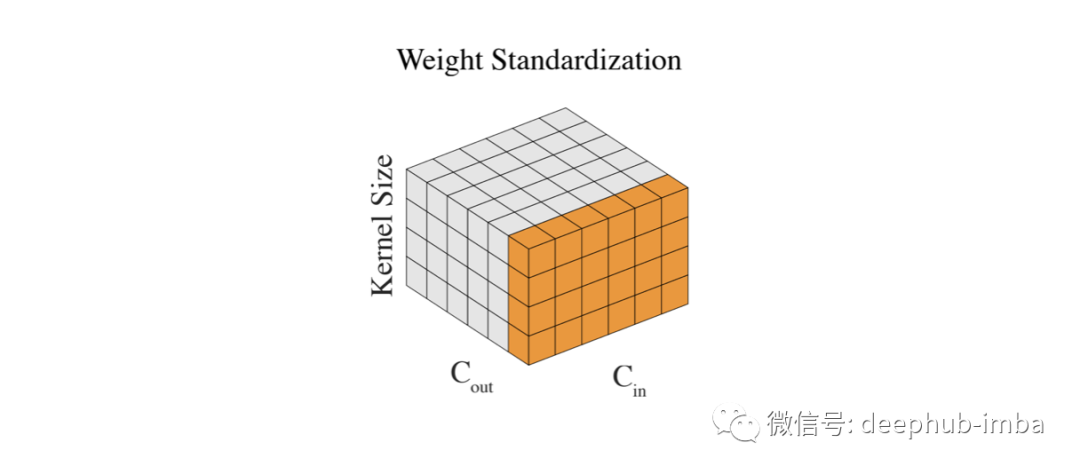
我們已經對輸入和層輸出進行了標準化，唯一剩下的就是權重。因為它們可以在沒有任何控制的情況下變大，尤其是當我們無論如何都要標準化輸出時。通過標準化權重，我們實現了更平滑的損失和更穩定的訓練。

def WeightStand(w, eps=1e-5): # w: input features shape [Cin, Cout, kernel_size, kernel_size] mean = torch.mean(input=w, dim=[0,2,3], keepdim=True) var = torch.var(input=w, dim=[0,2,3], keepdim=True) # mean, var shape : [1, Cout, 1, 1] w = (w - mean) / torch.sqrt(var + eps) return w

權重的標準化是Group Normalization的一個很好的輔助。在僅使用一個樣本的 BN（大批量）情況下，將這些方法結合起來會產生更好的結果。

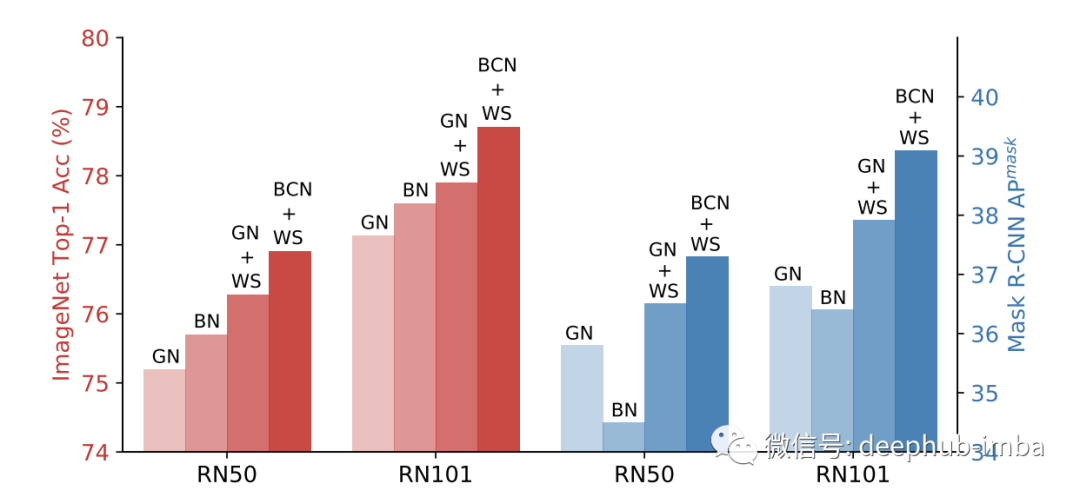
除此以外，有人還提出了BCN方法，稱為批處理通道規范化。簡而言之，每一層同時使用BN和GN。

總結

歸一化是深度學習中的一個基本概念。它加快了計算速度并穩定了訓練。多年來發展了許多不同的技術。本篇文章整理了目前與它相關的方法，希望對你有所幫助

審核編輯 ：李倩