穿越小说完本,小说阅读器,旷世神医

我們?cè)谏弦黄?/span>深度學(xué)習(xí)用于動(dòng)態(tài)系統(tǒng)建模（點(diǎn)擊跳轉(zhuǎn)）的文章中針對(duì)動(dòng)態(tài)系統(tǒng)的特性與數(shù)據(jù)驅(qū)動(dòng)的動(dòng)機(jī)進(jìn)行了論述。我們介紹了動(dòng)態(tài)系統(tǒng)當(dāng)前輸出不僅依賴于當(dāng)前的輸入，還依賴于系統(tǒng)過去的行為（歷史輸入和歷史輸出）。我們也介紹了什么場景下使用深度學(xué)習(xí)/系統(tǒng)辨識(shí)來進(jìn)行系統(tǒng)建模。本文我們主要介紹數(shù)據(jù)驅(qū)動(dòng)的另一個(gè)主題：系統(tǒng)辨識(shí)。為了更好地理解，我們可以設(shè)計(jì)一個(gè)簡單的線性系統(tǒng)[鏈接1]，更具體的是一個(gè)連續(xù)時(shí)間狀態(tài)空間模型，來解釋系統(tǒng)辨識(shí)的適用場景：

? 我們創(chuàng)建一個(gè)旋轉(zhuǎn)體的狀態(tài)空間模型，包括轉(zhuǎn)動(dòng)慣量J，阻尼力F和三個(gè)旋轉(zhuǎn)軸:

系統(tǒng)輸入 T 為驅(qū)動(dòng)扭矩。輸出 y 是旋轉(zhuǎn)體的角速度向量。將系統(tǒng)描述成狀態(tài)空間形式：

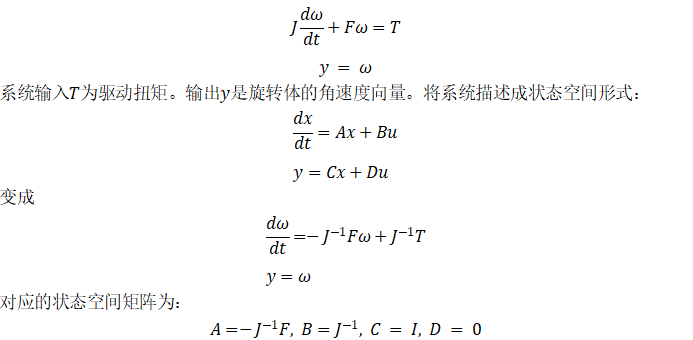
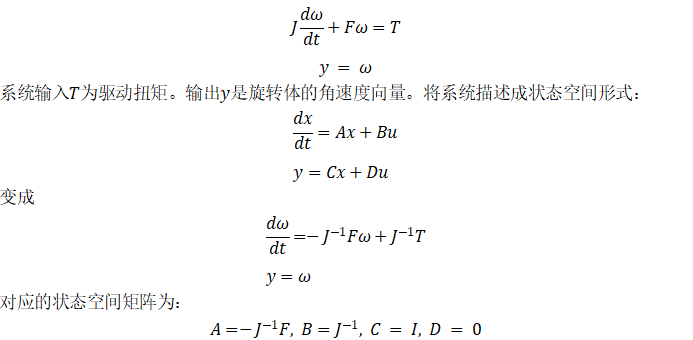變成

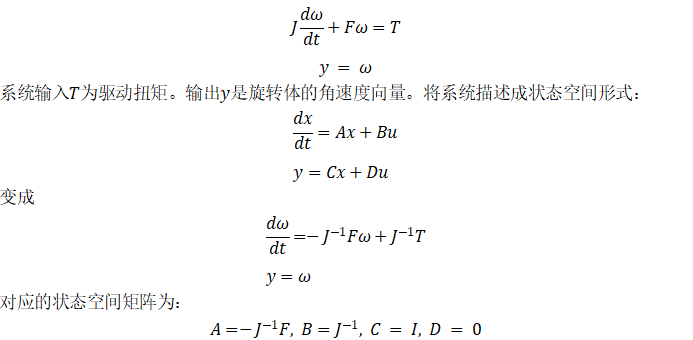
對(duì)應(yīng)的狀態(tài)空間矩陣為：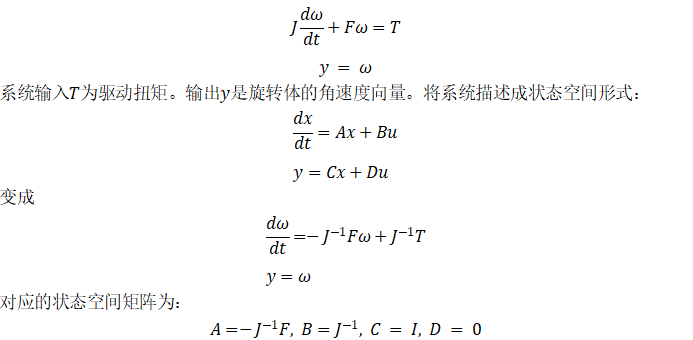

J = [8 -3 -3; -3 8 -3; -3 -3 8];

F = 0.2*eye(3);

A = -JF;

B = inv(J);

C = eye(3);

D = 0;

sys_mimo = ss(A,B,C,D);

?我們隨機(jī)生成控制輸入向量u的時(shí)間序列，作用于這個(gè)系統(tǒng)上，得到系統(tǒng)的輸出y。[鏈接2]

（滑動(dòng)窗口查看完整代碼）

% 構(gòu)建隨機(jī)步長的二值三維序列，N采樣數(shù)，Nu是控制量的維度

u = idinput([N,Nu],'prbs',frequency,Range);

for i = 1:Nu

% 為二值序列隨機(jī)賦值，得到不同幅值的序列

idx = find(diff(u(:,i))) + 1;

idx = [1;idx];

for j = 1:length(idx) - 1

u(idx(j):idx(j+1)-1,i) = randn*u(idx(j));

end

t = (1:N)*dt;

% 將控制輸入序列u作用系統(tǒng)上得到系統(tǒng)輸出

[y,t] = lsim(sys_mimo,u,t);

輸入 u=[u1 u2 u3] 應(yīng)三個(gè)維度的扭矩輸入，輸出對(duì)應(yīng) y=[y1 y2 y3] 三個(gè)維度的。如下：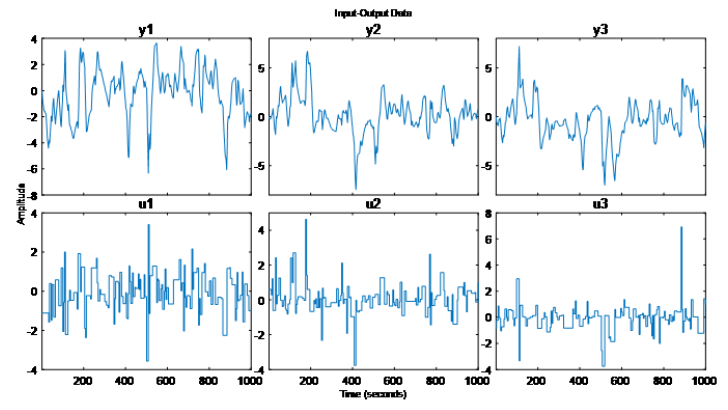

我們現(xiàn)在有系統(tǒng)的輸入 u，也有系統(tǒng)的輸出 y，這不就是數(shù)據(jù)科學(xué)的菜嗎，即使不知道系統(tǒng)模型，是不是也能“擬合”出來 y 和 u 的一個(gè)機(jī)器學(xué)習(xí)代理模型 (surrogate model)？我們工程中碰到的動(dòng)態(tài)系統(tǒng)通常也是可以獲取系統(tǒng)輸入和輸出，當(dāng)然比這個(gè)線性系統(tǒng)復(fù)雜多了，那能不能也用這種思路得到 y 和 u 的數(shù)據(jù)模型？接下來，是不是我們只需要把 y 和 u 作為輸出（真值）和輸入（特征）給到機(jī)器學(xué)習(xí)/深度學(xué)習(xí)算法，我們就能得到這樣一個(gè)動(dòng)態(tài)系統(tǒng)的數(shù)據(jù)模型呢？并非那么簡單。原因我們上一篇文章也解釋過，動(dòng)態(tài)系統(tǒng)的特殊性，狀態(tài)在時(shí)間維度上是有依賴的，并非某時(shí)刻有相同的控制輸入就有相同的狀態(tài)輸出，輸出也取決于當(dāng)前系統(tǒng)的狀態(tài)。我們不妨就用剛才的數(shù)據(jù) y 的第一個(gè)維度 y1 和 u，直接用幾種靜態(tài)機(jī)器學(xué)習(xí)算法對(duì)比動(dòng)態(tài)系統(tǒng)辨識(shí)算法來說明這種現(xiàn)象：a)使用高斯過程回歸進(jìn)行建模[鏈接3]

% 訓(xùn)練回歸模型

regressionGP = fitrgp(...

predictors,...

response,...

'BasisFunction','constant',...

'KernelFunction','rationalquadratic',...

'Standardize',true);

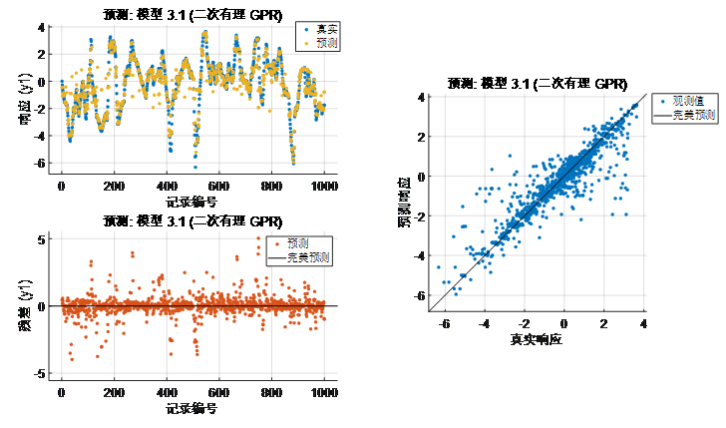圖表 1高斯過程回歸RMSE(Validation):0.7953a) 梯度提升集成回歸[鏈接4]

% 訓(xùn)練回歸模型

template = templateTree(...

'MinLeafSize',11, ...

'NumVariablesToSample',3);

regressionEnsemble = fitrensemble(...

predictors, ...

response, ...

'Method','LSBoost', ...

'NumLearningCycles',465, ...

'Learners', template,...

'LearnRate',0.2277131533235215);

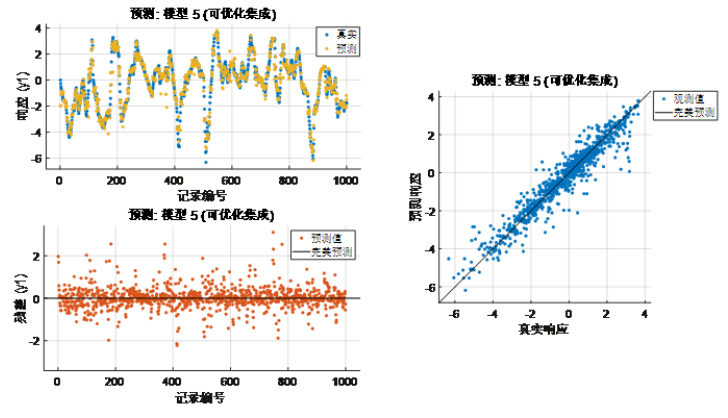圖表 2 梯度提升集成RMSE(Validation):0.5279從上面的高斯過程和梯度提升樹表現(xiàn)結(jié)果來看，雖然可以捕捉一些系統(tǒng)的特性，尤其梯度提升算法在精度上比高斯過程也有一定的提升，但誤差還是較大，系統(tǒng)瞬態(tài)特征被“平均”了。上述方式訓(xùn)練的機(jī)器學(xué)習(xí)靜態(tài)模型，在某瞬時(shí)只要輸入 u 是相同的，那么輸出 y 也是相同的，這與我們提到的動(dòng)態(tài)系統(tǒng)當(dāng)前時(shí)刻的輸出不止取決于輸入，還依賴于當(dāng)前系統(tǒng)狀態(tài)（換句話說即使在某個(gè)時(shí)刻相同的輸入，系統(tǒng)也可以有不同的輸出）的特性是不相符合的。當(dāng)然，可以通過一些特征衍生（例如不同尺度滑窗作用在輸入序列上生成新的特征等）的手段得到能夠反映狀態(tài)變化的多尺度特征用于模型訓(xùn)練，這樣的方式也使一些統(tǒng)計(jì)方法或機(jī)器學(xué)習(xí)模型或前饋神經(jīng)網(wǎng)絡(luò)等靜態(tài)模型可以用于動(dòng)態(tài)系統(tǒng)建模（上篇文章我們也介紹了電池、電機(jī)的使用示例）。b) 如果我們換個(gè)思路（系統(tǒng)辨識(shí)），假使我們提前已經(jīng)清楚這個(gè)系統(tǒng)可以用一個(gè)狀態(tài)空間模型表達(dá)，我們直接用動(dòng)態(tài)模型來“擬合”這個(gè)動(dòng)態(tài)系統(tǒng)，我們看看效果：nx = 3;sys = ssest(result,nx,'Ts',dt); % 進(jìn)行狀態(tài)空間模型系統(tǒng)辨識(shí)compare(result,sys) % 查看訓(xùn)練結(jié)果其實(shí)不必看結(jié)果我們也已經(jīng)估摸到結(jié)果可以達(dá)到100% 的準(zhǔn)確度，如下圖。當(dāng)然這個(gè)例子并非嚴(yán)謹(jǐn)，我們只看了訓(xùn)練過程，也沒有準(zhǔn)備測試數(shù)據(jù)，數(shù)據(jù)本身也沒有噪聲，但對(duì)于說明系統(tǒng)辨識(shí)的應(yīng)用場景還是比較直觀的。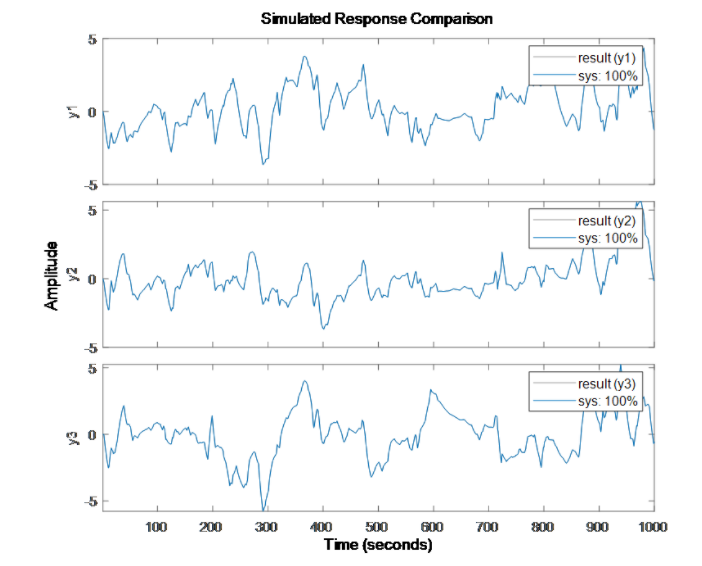

系統(tǒng)辨識(shí)利用測量得到的系統(tǒng)輸入和輸出信號(hào)來給那些不容易通過第一原理建模的動(dòng)態(tài)系統(tǒng)構(gòu)建數(shù)學(xué)模型。可以通過采集系統(tǒng)的輸入 - 輸出的時(shí)域和頻域數(shù)據(jù)來辨識(shí)連續(xù)時(shí)間或離散時(shí)間模型: 包括線性系統(tǒng)辨識(shí)，例如傳遞函數(shù)，過程模型，狀態(tài)空間模型，以及非線性系統(tǒng)動(dòng)態(tài)特性辨識(shí)，Hammerstein-Weiner 模型和 NARX（帶外部輸入的非線性自回歸，包含小波網(wǎng)絡(luò)，樹分類，sigmoid 網(wǎng)絡(luò)等）模型。另外，如果我們對(duì)系統(tǒng)結(jié)構(gòu)比較熟悉，也可以利用已有的理論定義含參的模型框架（微分方程），然后通過 Grey-Box 進(jìn)行模型參數(shù)辨識(shí)。辨識(shí)計(jì)算的過程就是模型參數(shù)迭代的過程（類似優(yōu)化算法），方法包括最大似然、預(yù)測誤差最小化 (PEM) 和子空間系統(tǒng)辨識(shí)。最后可以使用辨識(shí)好的模型進(jìn)行響應(yīng)預(yù)測與系統(tǒng)仿真。總結(jié)下來整個(gè)流程即：

接下來我們通過 MATLAB 自帶文檔示例（[鏈接5]，示例中提到了數(shù)據(jù)來源和參考文獻(xiàn)^[1]，Dr. Jiandong Wang 和 Dr. Akira Sano）來介紹上述提到的不同的模型。也鼓勵(lì)大家多多查閱幫助文檔。通過該示例，我們展示如何使用阻尼器的速度和阻尼力的測量數(shù)據(jù)來對(duì)系統(tǒng)創(chuàng)建線性、非線性 ARX 和 Hammerstein-Wiener 模型。

示例背景介紹和數(shù)據(jù)準(zhǔn)備

磁流變阻尼器是一種半主動(dòng)控制裝置，用于降低動(dòng)態(tài)結(jié)構(gòu)的振動(dòng)。磁流變液的粘度取決于輸入電壓/電流，因此可提供可控的阻尼力。為了研究這個(gè)系統(tǒng)的動(dòng)態(tài)性能，將磁流變阻尼器一端固定在地面上，另一端連接到振動(dòng)臺(tái)。每 0.005s 采樣一次阻尼力 f(t)。每 0.001s 采樣一次位移，用于在 0.005s 的采樣周期內(nèi)估計(jì)速度 v(t)。系統(tǒng)單輸入單輸出。輸入 v(t)為阻尼器的速度 [cm/s]，輸出為阻尼力 [N]。% F, V, Ts是load mrdamper.mat后加載的數(shù)據(jù)，將 F (output force), V (input% velocity) 和 Ts (sample time)封裝到iddata對(duì)象中.z = iddata(F, V, Ts,'Name', 'MR damper', ... 'InputName', 'v', 'OutputName', 'f',... 'InputUnit', 'cm/s', 'OutputUnit', 'N'); 將這個(gè)數(shù)據(jù)集 z 分成兩個(gè)子集，前 2000 個(gè)樣本 (ze) 用于估計(jì)/訓(xùn)練，其余的 (zv) 用于驗(yàn)證結(jié)果。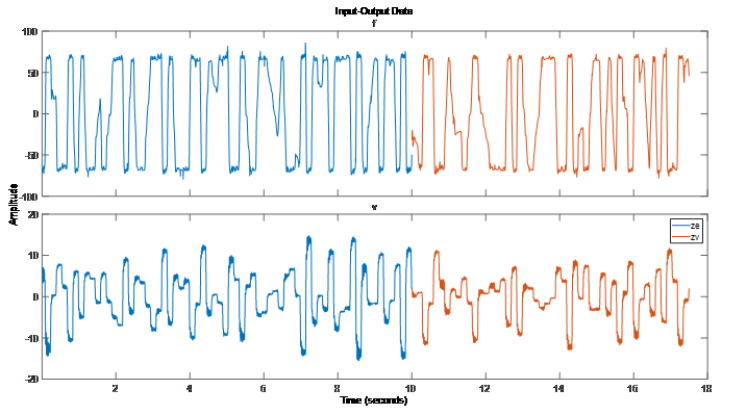

幾種線性系統(tǒng)模型

首先嘗試從簡單的線性模型開始。如果線性模型不能提供令人滿意的結(jié)果，那它也可以作為探索非線性模型的初值。ARX(Autoregressive with Extra Input) 模型ARX模型全稱帶外部輸入的自回歸(Autoregressive with Extra Input)。模型結(jié)構(gòu)方程：

模型中 y(t) 是系統(tǒng) t 時(shí)刻的輸出，自回歸是指模型中含有 y 自身的項(xiàng) y(t-1)···y(t-na)，na 對(duì)應(yīng)系統(tǒng)極點(diǎn)的個(gè)數(shù)，也就是 y(t) 和自身的 na 階有依賴，外部輸入項(xiàng) u(t-nk)+···+(t-nb-nk+1)是對(duì) y(t)產(chǎn)生影響的歷史輸入。其中 nk 是系統(tǒng)的延遲數(shù)，也就是 u(t)···u(t-nk+1) 這些項(xiàng)因?yàn)橄到y(tǒng)延遲還不會(huì)對(duì) y(t)產(chǎn)生影響，因此這些項(xiàng)不存在模型中。nb 是系統(tǒng)的零點(diǎn)個(gè)數(shù)，也就是輸入有 nb 階影響輸出。e(t) 是白噪音。模型一種更簡潔的寫法：

其中，q是單位延遲算子，

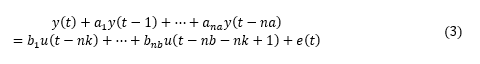
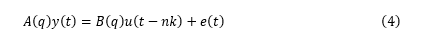
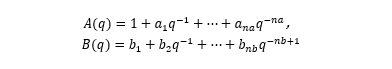?我們首先利用 ARX 模型來進(jìn)行模型階數(shù)推薦。階數(shù)的定義取決于模型的類型。通常模型最優(yōu)階數(shù)是通過試錯(cuò)得到的。但是線性 ARX 模型的階數(shù)可以通過 arxstruc 和 selstruc 等函數(shù)自動(dòng)計(jì)算出來。由此得到的階數(shù)也可以作為非線性模型嘗試使用的階數(shù)。我們先試著確定線性 ARX 模型的最優(yōu)階數(shù)。V = arxstruc(ze,zv,struc(1:5, 1:5,1:5));% 嘗試讓na, nb, nk在[1:5]取值Order = selstruc(V,'aic') % 根據(jù)Akaike's Information Criterion 選擇階數(shù)Order =2 4 1AIC 準(zhǔn)則選擇 Order = [na nb nk]=[2 4 1]，即在選擇的 ARX 模型結(jié)構(gòu)中，阻尼力 f(t) 使用 f(t-1)、f(t-2)、v(t-1)、v(t-2)、v(t-3)和v(t-4) 6 個(gè)回歸量 (regressor) 進(jìn)行預(yù)測。我們先按前面 selstruc 推薦的階數(shù)對(duì)應(yīng)的 ARX 模型進(jìn)行估計(jì)：LinMod1 = arx(ze, [2 4 1]);% ARX 模型 Ay = Bu + e, 形式同上面方程（4）OE 模型

這里先簡單介紹一下OE模型,它和傳遞函數(shù)相同，用多項(xiàng)式的比描述系統(tǒng)的輸入和輸出之間的關(guān)系。

模型階數(shù)等于分母多項(xiàng)式的階數(shù)。分母多項(xiàng)式的根稱為模型極點(diǎn)。分子多項(xiàng)式的根稱為模型零點(diǎn)。傳遞函數(shù)模型的參數(shù)是它的極點(diǎn)(階數(shù) nf)、零點(diǎn)(階數(shù) nb)和傳輸延遲(階數(shù) nk)。離散時(shí)間模型形式為:

對(duì)應(yīng)的階數(shù)：

連續(xù)時(shí)間 OE 或傳遞函數(shù)模型形式為：

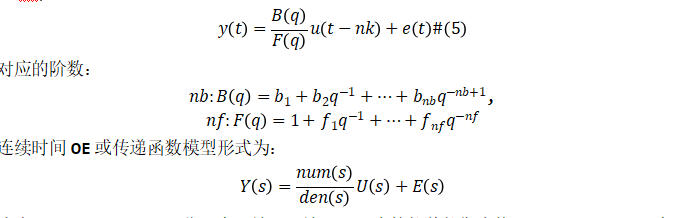
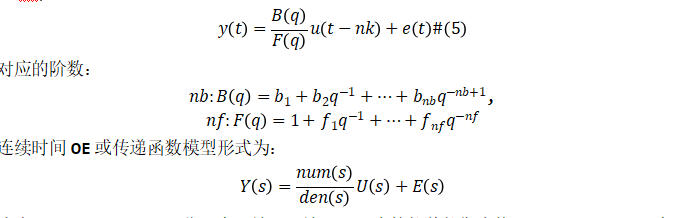
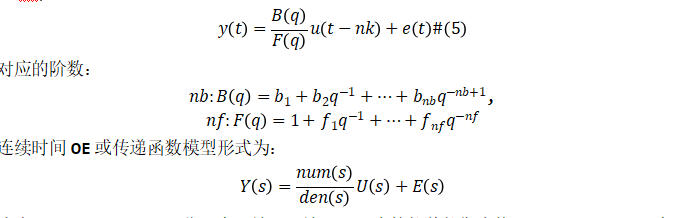
式中，Y(s)、U(s)、E(s) 分別表示輸出、輸入、噪聲的拉普拉斯變換。num(s)和 den(s)表示分子和分母多項(xiàng)式，定義了輸入和輸出之間的關(guān)系。

同樣我們用上面推薦的階數(shù)進(jìn)行輸出誤差模型(OE)估計(jì)。LinMod2 = oe(ze, [4 2 1]); % OE 模型 y = B/F u + e，形式同方程（5）

狀態(tài)空間模型

狀態(tài)空間模型用一組狀態(tài)變量的一階微分（連續(xù)時(shí)間）或差分（離散時(shí)間）方程來描述系統(tǒng)，而不是用一個(gè)或多個(gè) n 階微分或差分方程來描述系統(tǒng)。狀態(tài)變量 x(t) 可以從測量的輸入-輸出數(shù)據(jù)中抽象出來的，但在實(shí)驗(yàn)中它們本身不存在或不可測量的。狀態(tài)方程模型只需要你指定一個(gè)輸入,即這個(gè)模型階數(shù) n。模型階數(shù)等于 x(t) 的維數(shù)，它和對(duì)應(yīng)的線性差分方程中輸入輸出的延遲數(shù)相關(guān),但不一定相等。定義參數(shù)化狀態(tài)空間模型時(shí)，連續(xù)時(shí)間形式通常比離散時(shí)間形式容易，因?yàn)檫B續(xù)時(shí)間就跟你寫物理常微分方程類似。連續(xù)時(shí)間狀態(tài)空間模型有如下形式:

矩陣 F、G、H 和 D 具有一定的物理意義，例如和材料有關(guān)。K 包含擾動(dòng)矩陣。X0 代表初始狀態(tài)。可以使用時(shí)域和頻域數(shù)據(jù)來估計(jì)連續(xù)時(shí)間狀態(tài)空間模型。離散時(shí)間形式我們就不寫了，連續(xù)時(shí)間頻域數(shù)據(jù)不能用于估計(jì)離散時(shí)間狀態(tài)空間模型。回到問題本身，我們可以創(chuàng)建一個(gè)線性狀態(tài)空間模型，其階數(shù)(=狀態(tài)數(shù))將自動(dòng)確定:LinMod3 = ssest(ze);% 創(chuàng)建一個(gè) 3 階狀態(tài)空間模型 state-space model我們可以看一下這三個(gè)模型訓(xùn)練集和驗(yàn)證集上效果比較：

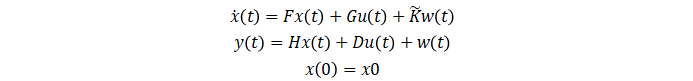
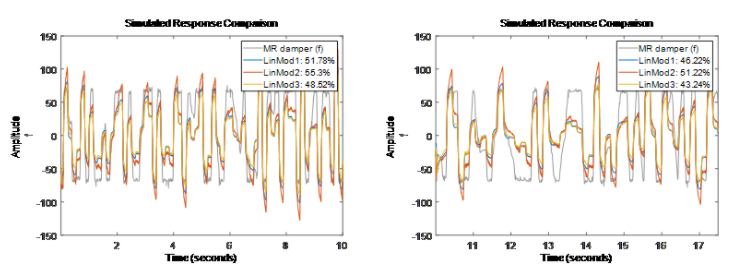
從驗(yàn)證集的結(jié)果看最好的模型擬合有 51% 的擬合度（擬合度即 NRMSE值，100(1-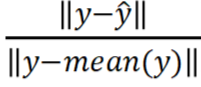），其中y是真實(shí)值，

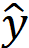?是模型預(yù)測值）。幾種非線性系統(tǒng)模型非線性 ARX 模型

前面的嘗試看上去線性模型精度還有待提高，我們嘗試用 Nonlinear ARX (IDNLARX)模型。我們也可以用 advice 函數(shù)來查看系統(tǒng)的輸入輸出數(shù)據(jù)的非線性程度。

advice(ze, 'nonlinearity') % 查看系統(tǒng)的非線性建議There is an indication of nonlinearity in the data.A nonlinear ARX model of order [4 4 1] and idTreePartition function performs better prediction of output than the corresponding ARX model of the same order. Consider using nonlinear models, such as IDNLARX, or IDNLHW. You may also use the "isnlarx" command to test for nonlinearity with more options.非線性ARX模型對(duì) ARX 做了一些擴(kuò)展。它在結(jié)構(gòu)中添加了非線性函數(shù)，如小波和 sigmoid 網(wǎng)絡(luò)，可以模擬復(fù)雜的非線性行為。對(duì)比線性 ARX 模型，見方程 (3)，我們重新組織一下方程 (3)，把當(dāng)前輸出 y(t)寫成過去輸出 + 當(dāng)前輸入 + 過去輸入之前權(quán)重和的形式, 我們把延遲數(shù) nk 先設(shè)置成 0，噪聲也不考慮，模型結(jié)構(gòu)簡化為：

u(t),y(t),e(t)分別是輸入，輸出和噪聲。y(t-1),y(t-2),···,y(t-na),u(t),u(t-1),···,u(t-nb-1) 是歷史輸出和延遲的輸入，他們看作 y(t) 的回歸量 (regressors,類似機(jī)器學(xué)習(xí)中的特征量，predictors)。系數(shù)矩陣 -a₁,···b_nb是作用在這些回歸量上的權(quán)重。線性 ARX 的輸出 y(t) 是這些回歸量的線性權(quán)重加和。對(duì)比線性 ARX，非線性 ARX 模型：

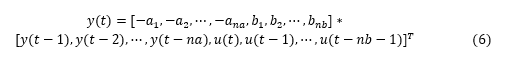
與方程 (6)不同處在于輸出 y(t)與回歸量之間的關(guān)系不是線性映射，而是一個(gè)非線性的映射 F。

F可以選擇不同的非線性函數(shù)，如小波網(wǎng)絡(luò)，多層前饋神經(jīng)網(wǎng)絡(luò)，樹分類。

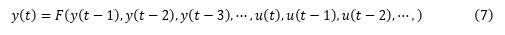
F 的輸入也就是模型的回歸量 (regressors)，這些回歸量對(duì)于線性 ARX 來說都是原始輸入和輸出的一些延遲項(xiàng)，非線性 ARX 則可以更復(fù)雜，可以是各種輸入輸出的非線性組合，例如：y(t-1)²,y(t-2)*u(t-1),abs(u(t-1)),max(y(t-3)*u(t-1),-10)。

我們通過一個(gè)結(jié)構(gòu)圖更形象的理解非線性 ARX 模型

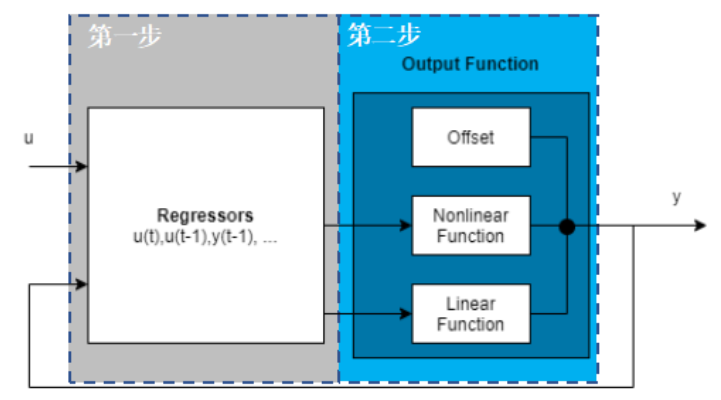主要通過兩步來計(jì)算輸出有 y(t)1. 根據(jù)當(dāng)前輸入 u(t)、歷史輸入 u(t-1)···、歷史輸出 y(t-1)··· 計(jì)算這些回歸量 (regressor) 的值。這些回歸量可以認(rèn)為就是對(duì)應(yīng)機(jī)器學(xué)習(xí)模型的特征量 (predictor)，可以是線性項(xiàng)，例如 u(t-1)，y(t-3),可以是多階多項(xiàng)式項(xiàng) u(t-1)²，也可以是一些自定義的變換后的非線性項(xiàng)，例如 u(t-1)*y(t-3)。你可以把這些回歸量作為輸入指定給模型中的線性函數(shù)或者非線性函數(shù)。2. 使用輸出函數(shù)（同時(shí)包含線性和非線性兩部分）將前面計(jì)算的回歸量 regressor 映射到輸出。例如下面這個(gè)函數(shù)：

式中 x 對(duì)應(yīng)著回歸量（regressor）向量，r 是 x 的均值。L^T(x-r)輸出函數(shù)的線性部分，g(Q(x-r))代表函數(shù)的非線性部分，Q 是一個(gè)投影矩。d 是一個(gè)補(bǔ)償偏置。F(x) 可以是任意非線性函數(shù)（小波網(wǎng)絡(luò)，多層感知機(jī)網(wǎng)絡(luò)，樹分類網(wǎng)絡(luò)），當(dāng)使用數(shù)據(jù)進(jìn)行模型辨識(shí)時(shí)，主要是通過迭代優(yōu)化來估計(jì)模型的參數(shù)值，例如 L,r,d,Q 以及網(wǎng)絡(luò) g 中的參數(shù)。接下來我們回到示例本身，嘗試創(chuàng)建非線性 ARX 模型，按我們上面提到的兩個(gè)步驟，我們首先來創(chuàng)建回歸量 (regressor)。簡化起見，我們主要使用 linearRegressor 來創(chuàng)建線性回歸量，可以通過階數(shù)矩陣 [na nb nk] 來方便創(chuàng)建，至于多階多項(xiàng)式回歸量（可以使用 polynomialRegressor 創(chuàng)建）或者自定義回歸量（可以試用 customRegressor 來創(chuàng)建）我們暫不探索。本示例我們主要通過探索不同的模型階數(shù)（上面介紹的階數(shù)矩陣 [na nb nk]）和不同的非線性映射函數(shù)（小波、sigmoid 網(wǎng)絡(luò)、樹分類等等）。

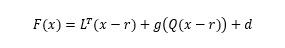
估計(jì)一個(gè)默認(rèn)的非線性 ARX 模型

Options = nlarxOptions('SearchMethod','lm');% 使用

LevenbergMarquardt作為估計(jì)算法

Options.SearchOptions.MaxIterations = 50;

Narx1 = nlarx(ze, [2 4 1], idSigmoidNetwork,Options)% 模型階數(shù)設(shè)置為 [2 4 1]，映射函數(shù)選擇 sigmoid 網(wǎng)絡(luò)，這個(gè)網(wǎng)絡(luò)用了一個(gè) sigmoid 函數(shù)和一個(gè)回歸量的線性權(quán)重和來計(jì)算輸出，nlarx 函數(shù)用來估計(jì)非線性 ARX 模型

disp(Narx1.OutputFcn)

Sigmoid NetworkInputs: f(t-1), f(t-2), v(t-1), v(t-2), v(t-3), v(t-4)Output: fNonlinear Function: Sigmoid network with 10 unitsLinear Function: initialized to [48.3 -3.38 -3.34 -2.7 -1.38 2.15]Output Offset: initialized to -18.9因?yàn)殡A數(shù)[na nb nk] = [2 4 1],所以模型回歸量包含 f(t-1),f(t-2),v(t-1),v(t-2),v(t-3),v(t-4)。此處 f 代表輸出，v 代表輸入。分別在訓(xùn)練集 ze 和驗(yàn)證集 zv 上進(jìn)行模型準(zhǔn)確度驗(yàn)證。

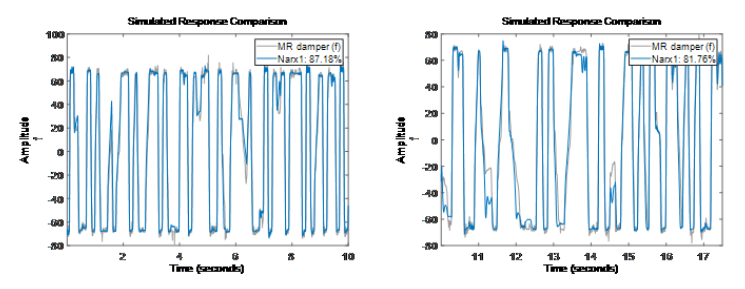通過結(jié)果可以看到，同樣的階數(shù)情況下，非線性 ARX 比線性模型的結(jié)果還是有提升。我們有很多可以嘗試的方向來測試不同的模型參數(shù)。

嘗試不同的模型階數(shù)

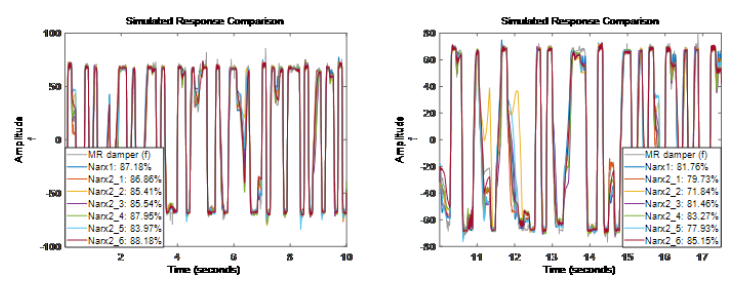圖表 3Narx2 為不同階數(shù)的模型在測試集上的結(jié)果從結(jié)果看出 Narx2{6} 模型對(duì)估計(jì)（訓(xùn)練）數(shù)據(jù)集和驗(yàn)證數(shù)據(jù)集的擬合結(jié)果都很好，同時(shí)階數(shù)比 Narx1 的要小。因此，我們將階數(shù)矩陣 [1 3 1] 作為后續(xù)試驗(yàn)的階數(shù)，同時(shí)將 Nlarx2{6} 作為參考進(jìn)行擬合比較。階數(shù)矩陣選擇對(duì)應(yīng)于使用 [f(t-1)， v(t-1)， v(t-2)， v(t-3)] 作為回歸量 (regressor) 集合。

嘗試修改 Sigmoid 網(wǎng)絡(luò)函數(shù)的隱含單元數(shù)

接下來我們嘗試修改 Sigmoid 網(wǎng)絡(luò)函數(shù)的隱含單元數(shù)。

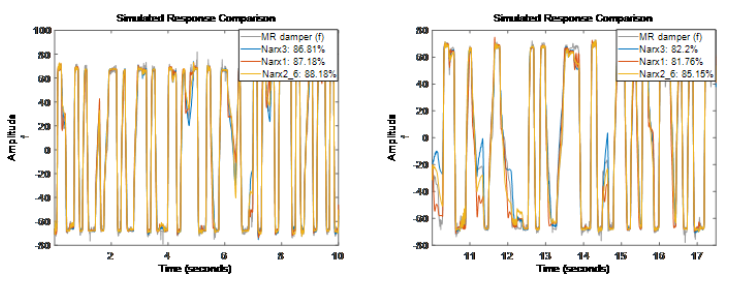看上去增加隱含單元數(shù)并沒有帶來精度提升 (Narx3結(jié)果不如Narx2{6})，所以我們?nèi)匀挥媚J(rèn) 10 個(gè)單元的 Sigmoid 網(wǎng)絡(luò)。

特征選擇：給非線性映射函數(shù)選擇回歸量子集

上面的示例中通過階數(shù)矩陣 ([na nb nk] = [1 3 1]) 定義的所有的回歸量都會(huì)作為非線性映射函數(shù)的輸入（此處用的 sigmoid 網(wǎng)絡(luò)）。但當(dāng)回歸量的數(shù)量很大時(shí)，會(huì)增加模型的復(fù)雜度。在不改變模型階數(shù)的情況下，可以只選擇一部分回歸量作為 sigmoid 網(wǎng)絡(luò)的輸入，可以通過 RegressorUsage 來控制特征選擇。它的值是一個(gè)表，它指定哪些函數(shù)使用哪些回歸量。例如，我們可以只把輸入變量相關(guān)的 v(t-1)，v(t-2)，v(t-3) 傳給非線性 sigmoid 函數(shù)而不需要 f(t-1)這可以通過以下方式實(shí)現(xiàn):Sig = idSigmoidNetwork(10);NarxInit = idnlarx(ze.OutputName, ze.InputName, [1 3 1], Sig);NarxInit.RegressorUsage.("f:NonlinearFcn")(1) = false; % 通過這個(gè)指定，回% 歸量 v(t-1), v(t-2), and v(t-3) 會(huì)被 sigmoid 函數(shù)使用，輸出回歸量 f(t-1) 則不會(huì)% 被 sigmoid 函數(shù)使用，idSigmoidNetwork也包含一個(gè)線性函數(shù)，這個(gè)函數(shù)則使用了所有% 的回歸量disp(NarxInit.RegressorUsage)Narx4 = nlarx(ze, NarxInit, Options);f:LinearFcn f:NonlinearFcn___________ ______________f(t-1) true false v(t-1) true true v(t-2) true true v(t-3) true true 創(chuàng)建另一個(gè)模型，僅使用回歸量 {y1(t-1)， u1(t-2)， u1(t-3)} 作為其非線性分量。Use = false(4,1);Use([1 3 4]) = true;NarxInit.RegressorUsage{:,2} = Use;% 指定 {y1(t-1)， u1(t-2)， u1(t-3)} 作為% 非線性輸入量Narx5 = nlarx(ze,NarxInit,Otions);

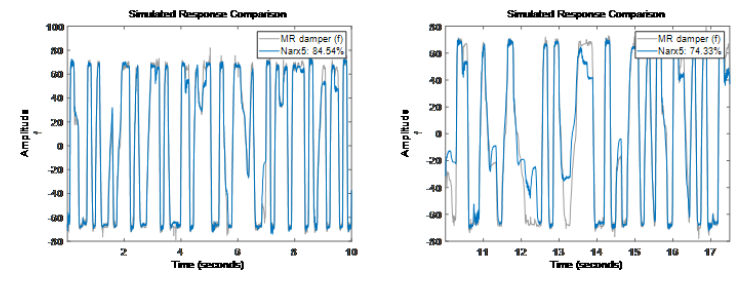看上去 Narx5 模型在估計(jì)數(shù)據(jù)和驗(yàn)證數(shù)據(jù)上表現(xiàn)還可以。

嘗試不同的非線性映射函數(shù)

我們這次使用小波網(wǎng)絡(luò)（對(duì)回歸量的線性映射和非線性映射兩部分中的非線性映射部分使用小波網(wǎng)絡(luò)）。NarxInit = idnlarx(ze.OutputName, ze.InputName, [1 3 1], idWaveletNetwork);% 僅使用回歸量 1 和 3 用于非線性網(wǎng)絡(luò)映射NarxInit.RegressorUsage.("f:NonlinearFcn")([2 4]) = false;Narx6 = nlarx(ze, NarxInit, Options);除了小波網(wǎng)絡(luò)，也可以使用樹分類非線性函數(shù)。TreeNet = idTreePartition;TreeNet.NonlinearFcn.NumberOfUnits = 20;NarxInit.OutputFcn = TreeNet;Narx7 = nlarx(ze, NarxInit, Options);將他們的結(jié)果和之前的Narx3，Narx5 結(jié)果進(jìn)行比較：

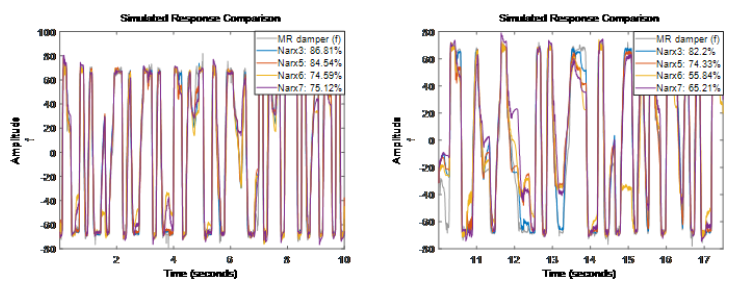從目前嘗試的結(jié)果看 Narx6 和 Narx7 模型的表現(xiàn)比 Narx5 還差一些。

分析估計(jì)出來的 IDNLARX 模型得到直觀解釋

我們通過前面的結(jié)果選擇比較好的模型，接下來可以使用 plot 和 resid 等命令進(jìn)一步分析來深入了解訓(xùn)練的模型的非線性特性，檢查模型 f(t) = F(f(t-1)， F(t-2)， v(t-1)，…，v(t-4)) 中非線性函數(shù) F 的截面。例如，在模型 Narx5 中，函數(shù) F 是一個(gè) sigmoid 網(wǎng)絡(luò)。為了探究 F() 作為回歸量 (regressor) 的函數(shù)的形狀，可以使用 PLOT 命令:plot(Narx5)

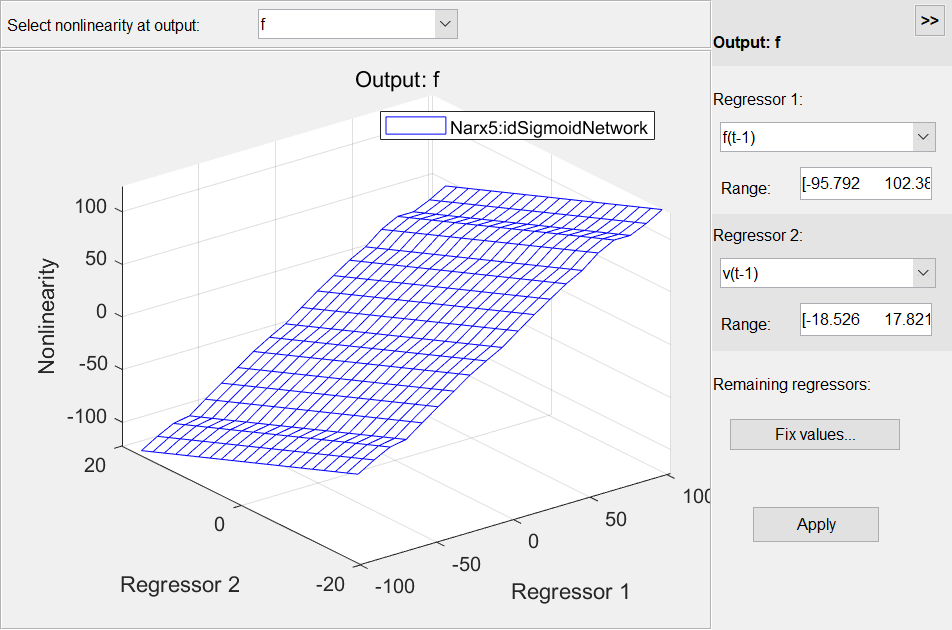plot 函數(shù)窗口提供了選擇繪制橫截面的回歸量及其范圍的選項(xiàng)。殘差檢驗(yàn) (residual test) 可用于進(jìn)一步模型分析。這個(gè)測試用于查看預(yù)測誤差是否為白噪聲且與輸入數(shù)據(jù)不相關(guān)。resid(zv, Narx3, Narx5)

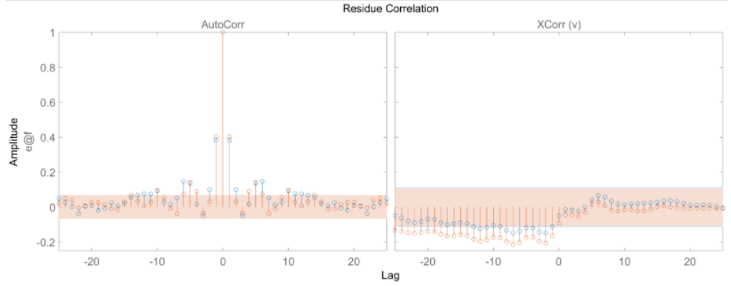殘差測試結(jié)果失敗可能是由于模型沒有捕捉到系統(tǒng)的動(dòng)態(tài)。從 Narx3 結(jié)果看殘差大多在 99% 的置信區(qū)間內(nèi)。非線性 ARX Hammerstein-Wiener模型Hammerstein-Wiener模型首先是一個(gè)非線性模型，但對(duì)于動(dòng)態(tài)部分，它其實(shí)是一個(gè)線性傳遞函數(shù)，那么非線性它怎么實(shí)現(xiàn)的?他其實(shí)是在輸入和輸出分別加了一個(gè)靜態(tài)的非線性變換，這樣通過一個(gè)先行傳遞函數(shù)來描述動(dòng)態(tài)特性再加上輸入和輸出的兩個(gè)靜態(tài)非線性函數(shù)，就組成了 Hammerstein-Wiener 模型。

圖中，f 是一個(gè)非線性函數(shù)，將輸入數(shù)據(jù) u(t) 轉(zhuǎn)換（靜態(tài)變換，t 時(shí)刻的輸出值只取決于 t 時(shí)刻的輸入值）為 w(t) = F (u(t))。B/F 是一個(gè)線性傳遞函數(shù)，將 w(t) 變換為 x(t) = (B/F)w(t)，這是動(dòng)態(tài)變換。B 和 F 類似于前面介紹的 OE 模型中的多項(xiàng)式。對(duì)于 ny 輸出和 nu 輸入，傳遞函數(shù)矩陣為:

其中，j = 1,2,……,ny和I = 1,2,…,nu 。h 是一個(gè)非線性函數(shù)，它將 x(t) 的輸出映射到(靜態(tài)變換)系統(tǒng)輸出 y(t)，即 y(t) = h (x(t))。我們使用和最開始 OE 模型 LinMod2 相同的階數(shù) (nb = 4, nf = 2, nk = 1) 來估計(jì)一個(gè) IDNLHW(Hammerstein-Wiener) 模型。使用 sigmoid 網(wǎng)絡(luò)作為 HW 模型非線性輸入和輸出。nlhw函數(shù)和其他估計(jì)函數(shù)（如 oe, nlarx 等函數(shù)）一樣。Opt = nlhwOptions('SearchMethod','lm');UNL = idSigmoidNetwork;YNL = idSigmoidNetwork;Nhw1 = nlhw(ze, [4 2 1], UNL, YNL, Opt)Nhw1 =Hammerstein-Wiener modelwith 1 output and 1 inputLinear transfer function corresponding to the orders nb = 4, nf = 2, nk = 1Input nonlinearity: Sigmoid network with 10 units Output nonlinearity: Sigmoid network with 10 unitsSample time: 0.005 secondsnhw1 模型在驗(yàn)證數(shù)據(jù)上有約 70% 的擬合度。

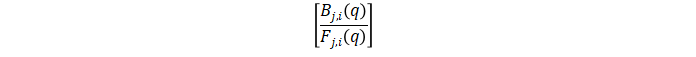
分析估計(jì)的 IDNLHW 模型

和非線性 ARX 模型類似，Hammerstein-Wiener 模型也可以使用 PLOT 命令檢查 I/O 非線性和中間部分線性傳函的特性。plot(Nhw1)

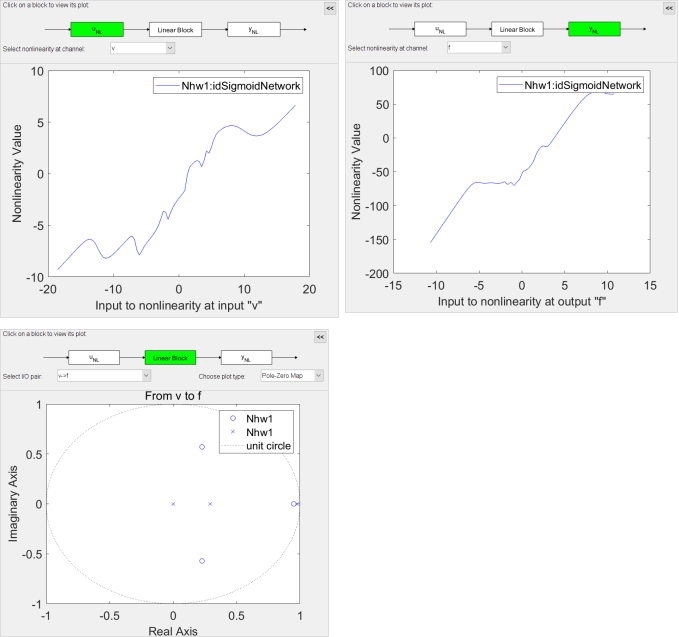從結(jié)果可以看出輸入非線性函數(shù)（像一個(gè)飽和函數(shù)）和輸出非線性函數(shù)（像一個(gè)分段線性函數(shù)）的形狀。線性傳函模塊的零極點(diǎn)圖中有一個(gè)零點(diǎn)和一個(gè)極點(diǎn)非常接近，說明可以去掉它們，從而減少模型的階數(shù)。接下來和 IDNLARX 一樣我們可以嘗試不同的模型參數(shù)，包括階數(shù)和輸入輸出的非線性函數(shù)。此處不在贅述，大家可以根據(jù)示例自由嘗試。

Conclusions 總結(jié)

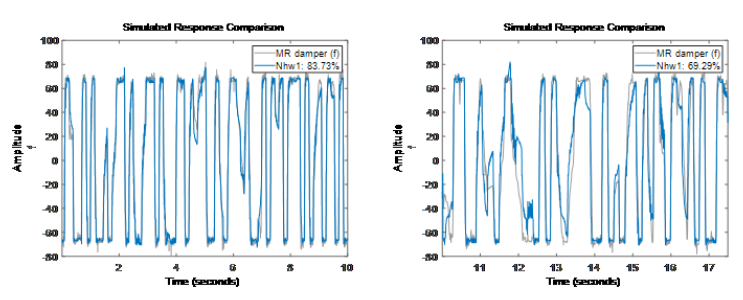
我們探索了各種非線性模型來表達(dá)輸入電壓和輸出阻尼力之間的動(dòng)態(tài)關(guān)系。結(jié)果表明，在非線性 ARX 模型中，Narx2{6} 和 Narx5 表現(xiàn)最好，而在 Hammerstein-Wiener 模型中，Nhw1 表現(xiàn)最好。非線性ARX模型最好的描述了 MR 阻尼器的動(dòng)態(tài)特性 (擬合度最好)。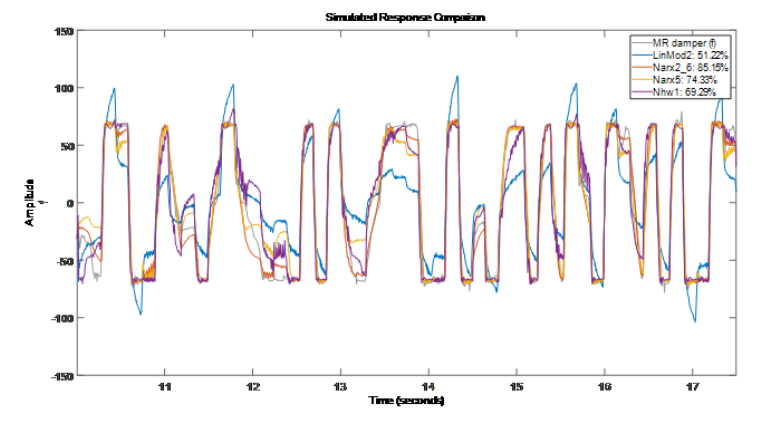

通過示例我們看到每種模型類型都有多個(gè)可用調(diào)項(xiàng)。例如對(duì)于非線性 ARX 模型，我們不僅可以指定模型的階數(shù)和非線性函數(shù)的類型，還可以修改和設(shè)置回歸量以及調(diào)整對(duì)應(yīng)函數(shù)的屬性。對(duì)于 Hammerstein-Wiener 模型，我們可以選擇輸入輸出非線性函數(shù)的類型，以及線性傳函的階數(shù)。因此使用數(shù)據(jù)辨識(shí)模型可以在對(duì)模型結(jié)構(gòu)或動(dòng)力學(xué)缺乏明確原理的情況下，嘗試各種選項(xiàng)，并分析它們對(duì)結(jié)果模型質(zhì)量的影響。當(dāng)然這個(gè)示例本身是單輸入單輸出（SISO，Single Input Single Output）的系統(tǒng), 對(duì)于多輸入多輸出（MIMO, Multi-Input Multi-Output）的系統(tǒng)上述大部分模型也都支持。具體的MIMO也可以查看文檔中更多的示例[鏈接6]。

附言：

系統(tǒng)辨識(shí)還有很多內(nèi)容文中示例沒有涉及，例如Grey-Box 模型估計(jì)，在線估計(jì)。附言中簡單介紹一下，也歡迎查閱相關(guān)詳細(xì)鏈接。

Grey-Box 模型

對(duì)于 Grey-Box 模型估計(jì)[鏈接7]，總體思想是說你已經(jīng)有了系統(tǒng)的微分/差分方程（線性，非線性）、狀態(tài)空間方程等等，但方程的系數(shù)是未知的，可以使用數(shù)據(jù)進(jìn)行方程系數(shù)的估計(jì)。這種估計(jì)的難點(diǎn)通產(chǎn)是構(gòu)建這個(gè)含參數(shù)的線性或非線性的系統(tǒng)方程。可以參考示例：包括車輛模型、電機(jī)模型、飛行器模型等等。

在線估計(jì)

在線估計(jì)[鏈接8]顧名思義就是說在物理系統(tǒng)（被控對(duì)象）運(yùn)行過程中，利用實(shí)時(shí)流數(shù)據(jù)不斷地對(duì)模型的參數(shù)和狀態(tài)進(jìn)行估計(jì)。

針對(duì)在線參數(shù)估計(jì)，主要使用迭代算法，利用當(dāng)前的實(shí)時(shí)測量數(shù)據(jù)和歷史的參數(shù)估計(jì)值來估計(jì)當(dāng)前模型（文章前面提到的模型）的參數(shù)值，算法迭代效率比較高，也可以支持嵌入式。
針對(duì)在線狀態(tài)估計(jì)，主要包含幾種狀態(tài)估計(jì)器，Kalman Filter（線性系統(tǒng)），Extended Kalman Filter（可線性化的非線性系統(tǒng)），Unscented Kalman Filter（非線性系統(tǒng)）， Particle Filter （類似 UKF）等。

原文標(biāo)題：數(shù)據(jù)驅(qū)動(dòng)的動(dòng)態(tài)系統(tǒng)（Dynamical System）建模(二)：系統(tǒng)辨識(shí)

文章出處：【微信公眾號(hào)：MATLAB】歡迎添加關(guān)注！文章轉(zhuǎn)載請(qǐng)注明出處。

審核編輯：湯梓紅

聲明：本文內(nèi)容及配圖由入駐作者撰寫或者入駐合作網(wǎng)站授權(quán)轉(zhuǎn)載。文章觀點(diǎn)僅代表作者本人，不代表電子發(fā)燒友網(wǎng)立場。文章及其配圖僅供工程師學(xué)習(xí)之用，如有內(nèi)容侵權(quán)或者其他違規(guī)問題，請(qǐng)聯(lián)系本站處理。舉報(bào)投訴

數(shù)據(jù)驅(qū)動(dòng)

數(shù)據(jù)驅(qū)動(dòng)

+關(guān)注

關(guān)注
0

文章
127

瀏覽量
12339
系統(tǒng)辨識(shí)

系統(tǒng)辨識(shí)

+關(guān)注

關(guān)注
0

文章
11

瀏覽量
7283
動(dòng)態(tài)系統(tǒng)

動(dòng)態(tài)系統(tǒng)

+關(guān)注

關(guān)注
0

文章
4

瀏覽量
5244