K-means 算法是典型的基于距離的聚類算法，采用距離作為相似性的評價指標，兩個對象的距離越近，其相似度就越大。而簇是由距離靠近的對象組成的，因此算法目的是得到緊湊并且獨立的簇。

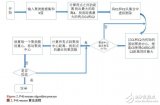
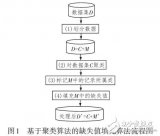
假設要將對象分成 k 個簇，算法過程如下：

(1) 隨機選取任意 k 個對象作為初始聚類的中心（質心，Centroid），初始代表每一個簇；

(2) 對數據集中剩余的每個對象根據它們與各個簇中心的距離將每個對象重新賦給最近的簇；

(3) 重新計算已經得到的各個簇的質心；

(4) 迭代步驟(2)-(3)直至新的質心與原來的質心相等或小于設定的閾值，算法結束。

注意！

(1) 在 K-means 算法 k 值通常取決于人的主觀經驗；

(2) 距離公式常用歐氏距離和余弦相似度公式，前者是根據位置坐標直接計算的，主要體現個體數值特征的差異，而后者更多體現了方向上的差異而不是位置上的，cosθ越接近 1 個體越相似，可以修正不同度量標準不統一的問題；

(3) K-means 算法獲得的是局部最優解，在算法中，初始聚類中心常常是隨機選擇的，一旦初始值選擇的不好，可能無法得到有效的聚類結果。

對于一堆數據，K 值（簇數）的最優解如何確定呢？常見的有“肘”方法

（Elbow method）和輪廓系數法（Silhouette Coeffient）：

① “肘”方法：核心指標是 SSE（sum of the squared errors，誤差平方和），即所有樣本的聚類誤差（累計每個簇中樣本到質心距離的平方和），隨著 K 的增大每個簇聚合度會增強，SSE 下降幅度會增大，隨著 K 值繼續增大 SSE 的下降幅度會減少并趨于平緩，SSE 和 K 值的關系圖會呈現成一個手肘的形狀，此肘部對應的 K 值就是最佳的聚類數。

② 輪廓系數法：結合聚類的凝聚度（Cohesion）和分離度（Separation）來考慮，凝聚度為樣本與同簇其他樣本的平均距離，分離度為樣本與最近簇中所有樣本的平均距離，該值處于-1~1 之間，值越大表示聚類效果越好。

以 iris 數據為例：

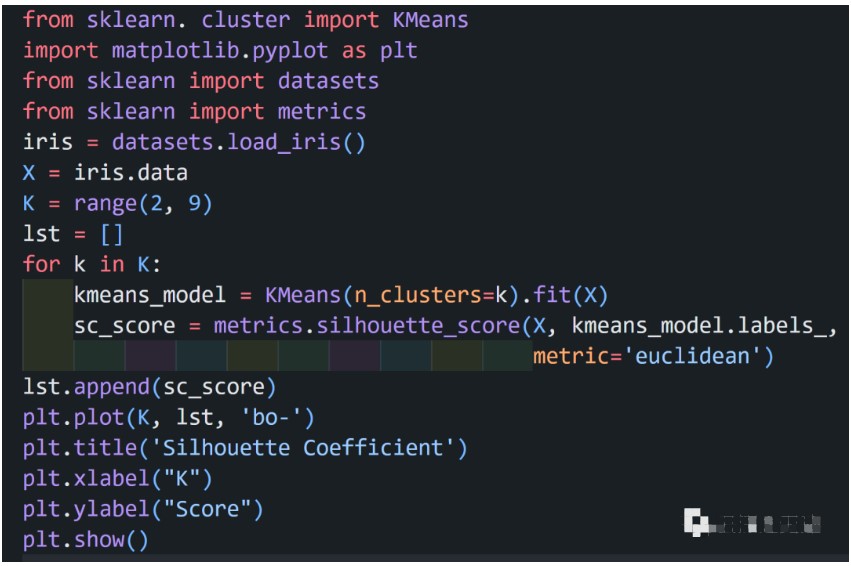
代碼實現

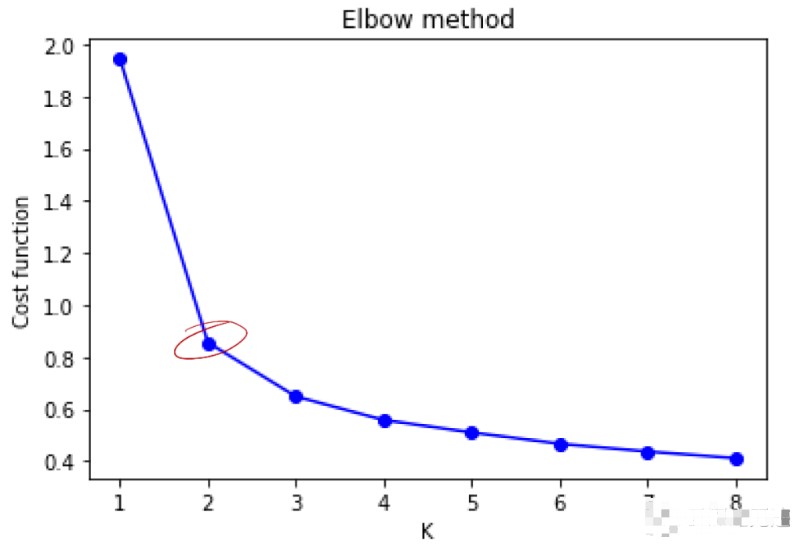
由圖看出拐點在 K=2 處，K=3 次之，iris 實際數據分成了三類。