線性反饋移位寄存器(LFSR):通常由移位寄存器和異或門邏輯組成。其主要應用在:偽隨機數,偽噪聲序列,計數器,BIST,數據的加密和CRC校驗等。
Part.1
線性反饋移位寄存器(LFSR)主要包括兩大類:斐波那契(外部LFSR),又稱many-to-one;伽羅瓦(內部LFSR),又稱one-to-many。
如下圖(模2的多項式:x^8+x^6+x^4+1):
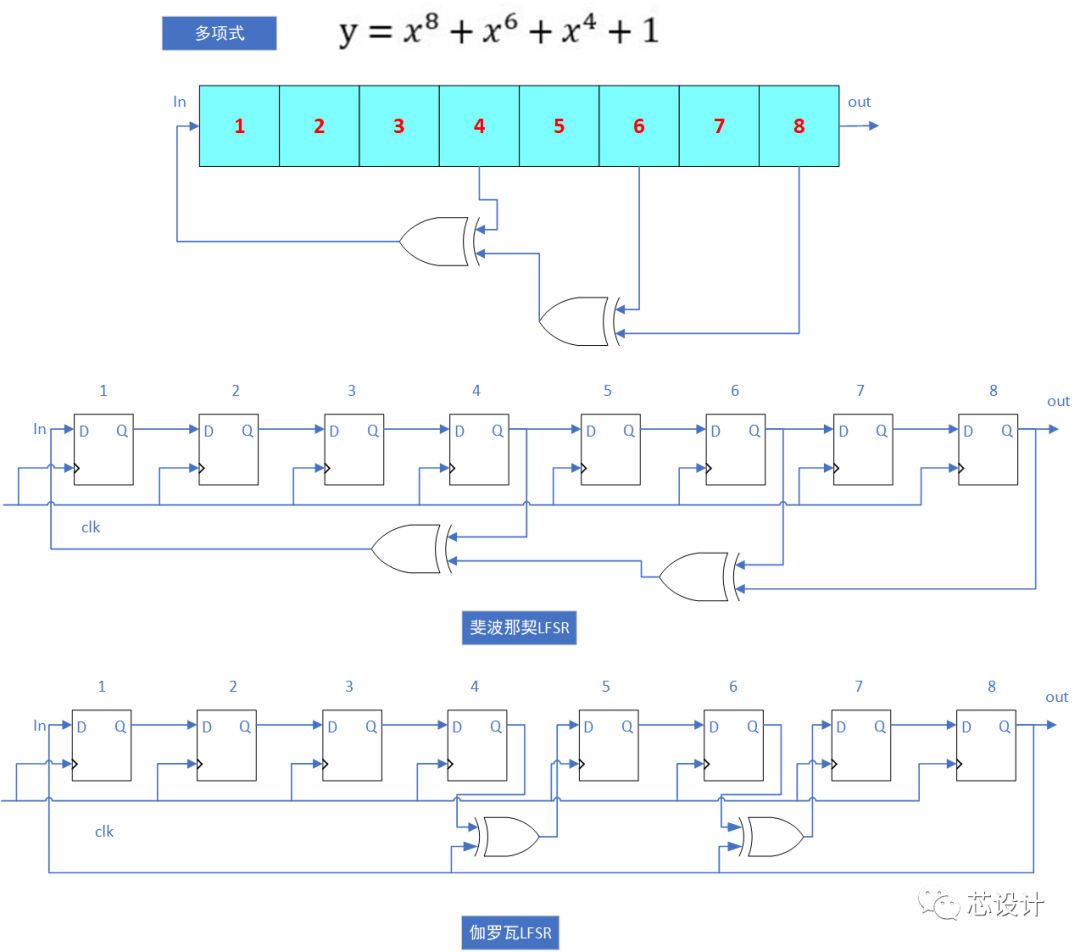
Part.2
抽頭(tap):影響線性反饋寄存器下一個狀態的比特位叫做抽頭,抽頭的設定會決定線性反饋寄存器最大的輸出序列長度,抽頭通常用有限域算數中模2的多項式來表示(例如模2的多項式為:x^8+x^6+x^4+1)。通常N bits的線性反饋寄存器能產生最長的不重復序列為2^N-1。因為當所有寄存器的輸出為全零狀態時,線性反饋寄存器陷入死循環,故Nbit的線性反饋寄存器的輸出狀態有2^N-1。抽頭的位置會影響LSFR的最大輸出狀態的個數,例如:3bit的抽頭為【3,2】會產生7個狀態(多項式對應為:x^3+x^2+1),若抽頭為【3,1】會產生2個狀態(多項式對應為:x^3+x+1)。當N bits下,抽頭的設定產生的最大輸出序列長度為2^N-1時,此時對應的模2多項式為本原多項式。下表為不同的bits下,抽頭的設定(對應不同的本原多項式)和最大的輸出狀態個數關系表。
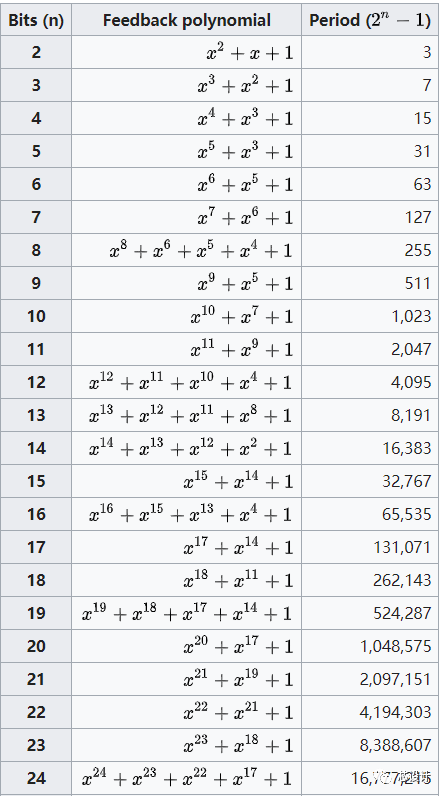
Part.3
上面提到N bits的LFSR能產生最大輸出狀態的個數為2^N-1,如果輸出狀態包括全零的狀態,最大輸出狀態的個數可達到2^N,那么通過對LFSR做如下圖的修改,即如果檢測到Q[7]-Q[0]輸出狀態為全零時,經過~|Q[6:0]^Q[7]邏輯運算后輸出的結果為1,進而保證線性反饋寄存器不會陷入死循環中。
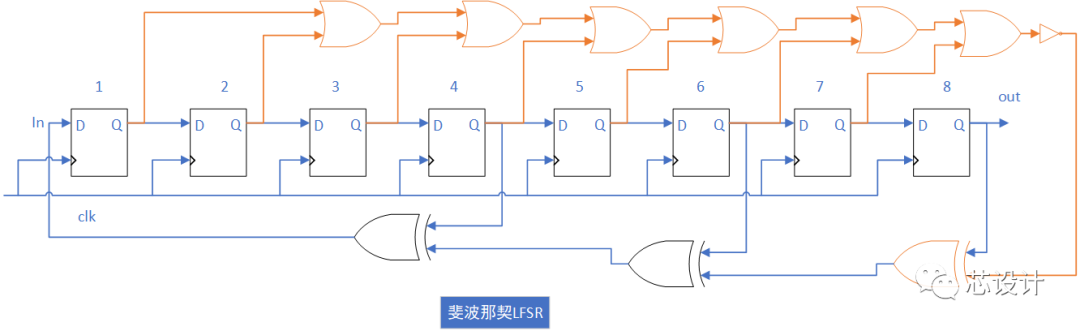
Part.4
在實際的應用中,例如crc的校驗,會用到模2的多項式的運算,遵循如下的計算原則:

寫在最后
這里只是介紹了線性反饋移位寄存器的原理,后面會講到RTL的實現。
審核編輯:郭婷
-
寄存器
+關注
關注
31文章
5343瀏覽量
120379 -
計數器
+關注
關注
32文章
2256瀏覽量
94575
原文標題:線性反饋移位寄存器原理
文章出處:【微信號:zhuyandz,微信公眾號:FPGA之家】歡迎添加關注!文章轉載請注明出處。
發布評論請先 登錄
相關推薦
移位寄存器的工作原理、類型及應用
移位寄存器中使用的儲存單元是什么
移位寄存器中Dsr有什么用
移位寄存器右移是怎么移位的
PLC移位寄存器指令的工作過程
8位移位寄存器工作原理是什么?
移位寄存器的工作原理與作用
雙向移位寄存器的工作原理、特點及應用
移位寄存器的功能是什么 移位寄存器的工作原理
線性反饋移位寄存器輸出序列怎么算
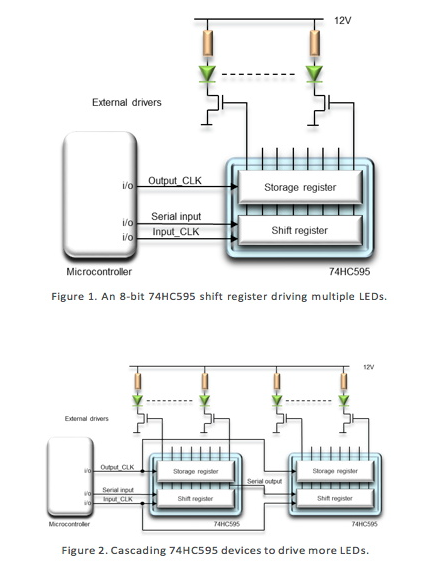
移位寄存器可降低LED設計的尺寸和成本




 線性反饋移位寄存器原理
線性反饋移位寄存器原理











評論