之前面試,被問到一道非常經典且非常實用的算法題目:會議室安排問題。
力扣上類似的問題是會員題目,你可能沒辦法做,但對于這種經典的算法題,掌握思路還是必要的。
先說下題目,給你輸入若干形如[begin, end]的區間,代表若干會議的開始時間和結束時間,請你計算至少需要申請多少間會議室。
函數簽名如下:
//返回需要申請的會議室數量
intminMeetingRooms(int[][]meetings);
比如給你輸入meetings = [[0,30],[5,10],[15,20]],算法應該返回 2,因為后兩個會議和第一個會議時間是沖突的,至少申請兩個會議室才能讓所有會議順利進行。
如果會議之間的時間有重疊,那就得額外申請會議室來開會,想求至少需要多少間會議室,就是讓你計算同一時刻最多有多少會議在同時進行。
換句話說,如果把每個會議的起止時間看做一個線段區間,那么題目就是讓你求最多有幾個重疊區間,僅此而已。
對于這種時間安排的問題,本質上講就是區間調度問題,十有八九得排序,然后找規律來解決。
題目延伸
我們之前寫過很多區間調度相關的文章,這里就順便幫大家梳理一下這類問題的思路:
第一個場景,假設現在只有一個會議室,還有若干會議,你如何將盡可能多的會議安排到這個會議室里?
這個問題需要將這些會議(區間)按結束時間(右端點)排序,然后進行處理,詳見前文貪心算法做時間管理。
第二個場景,給你若干較短的視頻片段,和一個較長的視頻片段,請你從較短的片段中盡可能少地挑出一些片段,拼接出較長的這個片段。
這個問題需要將這些視頻片段(區間)按開始時間(左端點)排序,然后進行處理,詳見前文剪視頻剪出一個貪心算法。
第三個場景,給你若干區間,其中可能有些區間比較短,被其他區間完全覆蓋住了,請你刪除這些被覆蓋的區間。
這個問題需要將這些區間按左端點排序,然后就能找到并刪除那些被完全覆蓋的區間了,詳見前文刪除覆蓋區間。
第四個場景,給你若干區間,請你將所有有重疊部分的區間進行合并。
這個問題需要將這些區間按左端點排序,方便找出存在重疊的區間,詳見前文合并重疊區間。
第五個場景,有兩個部門同時預約了同一個會議室的若干時間段,請你計算會議室的沖突時段。
這個問題就是給你兩組區間列表,請你找出這兩組區間的交集,這需要你將這些區間按左端點排序,詳見前文區間交集問題。
第六個場景,假設現在只有一個會議室,還有若干會議,如何安排會議才能使這個會議室的閑置時間最少?
這個問題需要動動腦筋,說白了這就是個 0-1 背包問題的變形:
會議室可以看做一個背包,每個會議可以看做一個物品,物品的價值就是會議的時長,請問你如何選擇物品(會議)才能最大化背包中的價值(會議室的使用時長)?
當然,這里背包的約束不是一個最大重量,而是各個物品(會議)不能互相沖突。把各個會議按照結束時間進行排序,然后參考前文0-1 背包問題詳解的思路即可解決,等我以后有機會可以寫一寫這個問題。
第七個場景,就是本文想講的場景,給你若干會議,讓你合理申請會議室。
好了,舉例了這么多,來看看今天的這個問題如何解決。
題目分析
重復一下題目的本質:
給你輸入若干時間區間,讓你計算同一時刻「最多」有幾個區間重疊。
題目的關鍵點在于,給你任意一個時刻,你是否能夠說出這個時刻有幾個會議在同時進行?
如果可以做到,那我遍歷所有的時刻,找個最大值,就是需要申請的會議室數量。
有沒有一種數據結構或者算法,給我輸入若干區間,我能知道每個位置有多少個區間重疊?
老讀者肯定可以聯想到之前說過的一個算法技巧:差分數組技巧。
把時間線想象成一個初始值為 0 的數組,每個時間區間[i, j]就相當于一個子數組,這個時間區間有一個會議,那我就把這個子數組中的元素都加一。
最后,每個時刻有幾個會議我不就知道了嗎?我遍歷整個數組,不就知道至少需要幾間會議室了嗎?
舉例來說,如果輸入meetings = [[0,30],[5,10],[15,20]],那么我們就給數組中[0,30],[5,10],[15,20]這幾個索引區間分別加一,最后遍歷數組,求個最大值就行了。
還記得嗎,差分數組技巧可以在 O(1) 時間對整個區間的元素進行加減,所以可以拿來解決這道題。
不過,這個解法的效率不算高,所以我這里不準備具體寫差分數組的解法,參照差分數組技巧的原理,有興趣的讀者可以自己嘗試去實現。
基于差分數組的思路,我們可以推導出一種更高效,更優雅的解法。
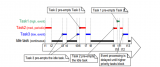
我們首先把這些會議的時間區間進行投影:
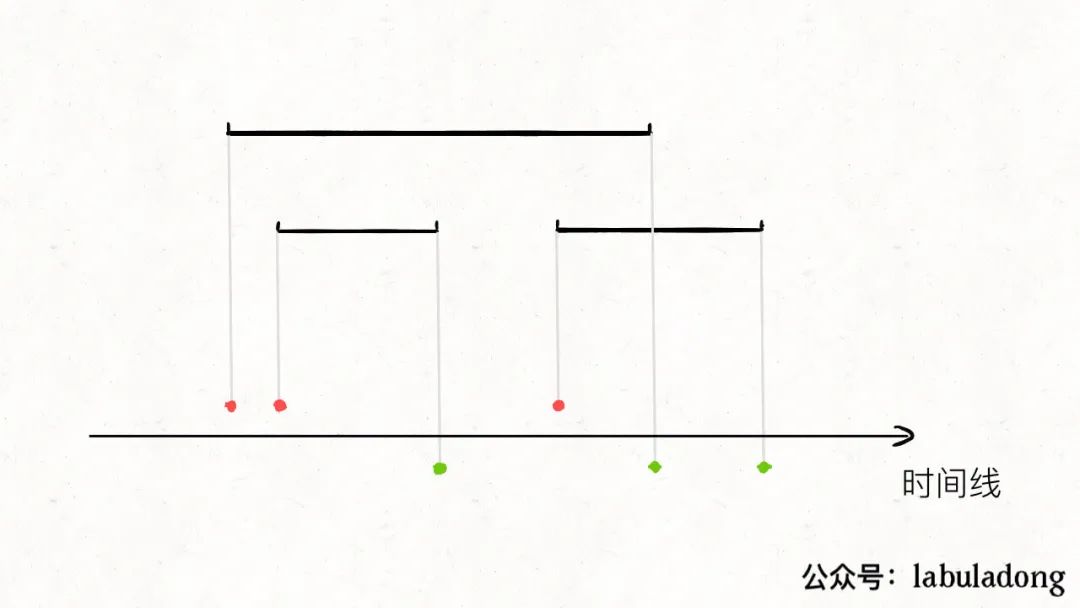
紅色的點代表每個會議的開始時間點,綠色的點代表每個會議的結束時間點。
現在假想有一條帶著計數器的線,在時間線上從左至右進行掃描,每遇到紅色的點,計數器count加一,每遇到綠色的點,計數器count減一:
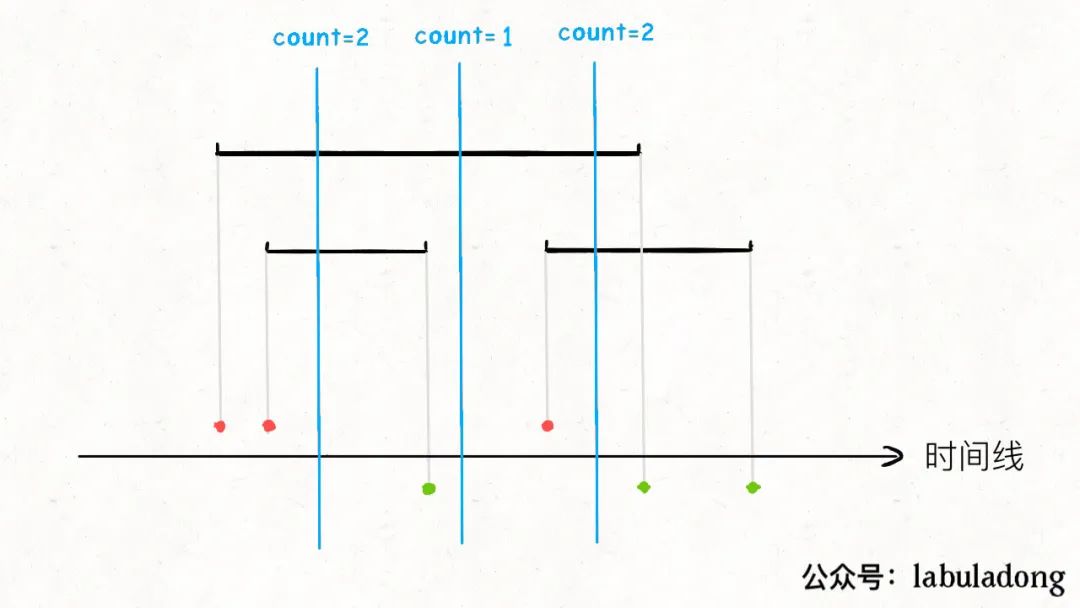
這樣一來,每個時刻有多少個會議在同時進行,就是計數器count的值,count的最大值,就是需要申請的會議室數量。
對差分數組技巧熟悉的讀者一眼就能看出來了,這個掃描線其實就是差分數組的遍歷過程,所以我們說這是差分數組技巧衍生出來的解法。
代碼實現
那么,如何寫代碼實現這個掃描的過程呢?
首先,對區間進行投影,就相當于對每個區間的起點和終點分別進行排序:

intminMeetingRooms(int[][]meetings){
intn=meetings.length;
int[]begin=newint[n];
int[]end=newint[n];
//把左端點和右端點單獨拿出來
for(inti=0;i0];
end[i]=meetings[i][1];
}
//排序后就是圖中的紅點
Arrays.sort(begin);
//排序后就是圖中的綠點
Arrays.sort(end);
//...
}
然后就簡單了,掃描線從左向右前進,遇到紅點就對計數器加一,遇到綠點就對計數器減一,計數器count的最大值就是答案:
intminMeetingRooms(int[][]meetings){
intn=meetings.length;
int[]begin=newint[n];
int[]end=newint[n];
for(inti=0;i0];
end[i]=meetings[i][1];
}
Arrays.sort(begin);
Arrays.sort(end);
//掃描過程中的計數器
intcount=0;
//雙指針技巧
intres=0,i=0,j=0;
while(iif(begin[i]//掃描到一個紅點
count++;
i++;
}else{
//掃描到一個綠點
count--;
j++;
}
//記錄掃描過程中的最大值
res=Math.max(res,count);
}
returnres;
}
這里使用的是雙指針技巧,你可以認為指針i就是那根掃描線,根據i, j的相對位置就可以模擬掃描線前進的過程。
至此,這道題就做完了。當然,這個題目也可以變形,比如給你若干會議,問你k個會議室夠不夠用,其實你套用本文的解法代碼,也可以很輕松解決。
審核編輯 :李倩
-
算法
+關注
關注
23文章
4625瀏覽量
93143 -
數組
+關注
關注
1文章
417瀏覽量
25994
原文標題:時間調度問題的千層套路
文章出處:【微信號:TheAlgorithm,微信公眾號:算法與數據結構】歡迎添加關注!文章轉載請注明出處。
發布評論請先 登錄
相關推薦
Linux之CPU調度策略和CPU親和性

算力調度的基礎知識

Linux調度器的核心scheduler_tick介紹
FPGA-5G通信算法的基本套路
深入探討Linux的進程調度器

車輛調度系統

TSMaster 自定義 LIN 調度表編程指導

如何實現上位機靈活調度下位機?
什么是時間片輪轉調度?時間片輪轉調度算法基本原理
鴻蒙OS 分布式任務調度
Linux的Deadline實時調度算法





 時間調度問題的千層套路
時間調度問題的千層套路











評論