1.m序列簡介

m序列是目前廣泛應用的一種偽隨機序列，其在通信領域有著廣泛的應用，如擴頻通信，衛星通信的碼分多址，數字數據中的加密、加擾、同步、誤碼率測量等領域。m序列在所有的偽隨機序列里面的地位是最基礎同樣也是最重要的。它的特點就是產生方便快捷，有很強的規律特性，同時自相關性、互相關特性也很好。在IS-95的反向信道中，選擇了m序列的PN碼作為地址碼，利用不同相位m序列幾乎正交的特性來為每個用戶的業務信道分配了一個相位 。簡單來說，n級反饋移位寄存器的狀態最多由2^n 個，同時，在線性的反饋移位寄存器中，全“0”狀態永不改變，所以也就是說，它的最長的周期就是 2^n - 1。

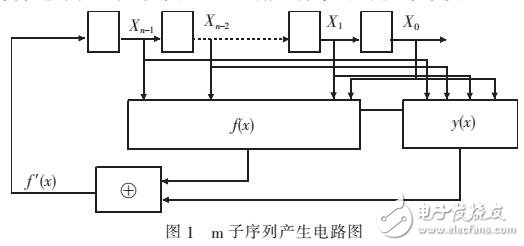
由于反饋的存在，移存器的輸入端受控地輸入信號。不難看出，若初始狀態為全“0”,則移位后得到的仍為全“0”，因此應避免出現全“0”狀態，又因為n級移存器共有2n-1種可能的不同狀態，除全“0”狀態外，剩下2n-1種狀態可用。每移位一次，就出現一種狀態，在移位若干次后，一定能重復出現前某一狀態，其后的過程便周而復始了。反饋線位置不同將出現不同周期的不同序列，我們希望找到線性反饋的位置，能使移存器產生的序列最長，即達到周期P=2^n-1。

2.m序列性質

周期為2^n-1的m序列由以下幾個特點：

①隨機性

在m序列的一個周期中，0和1出現概率大致相同，0碼只比1碼多一個。

②移位可加性

某個周期為p的m序列與其經任意延遲移位后的序列模2相加后，其結果仍是周期為p的m序列，只是原序列某次延遲移位后的序列。

③預先可確定性

m序列是由移位寄存器的初始狀態和反饋網絡唯一確定的。

④游程特性

序列中取值相同的相繼元素稱為一個游程。游程長度指的是游程中元素的個數。在m序列中，一共有個游程。其中長度為1的游程占總游程數的一半；長度為2的游程占總游程的1/4；長度為k的游程占總游程數的，且在長度為k的游程中，連0與連1的游程數各占一半。另外，還有一個長度為n的1游程和一個長度為(n一1)的0游程。

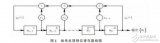
3.線性移位反饋寄存器的結構圖如下：

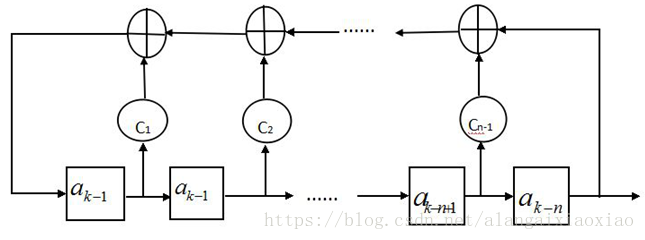
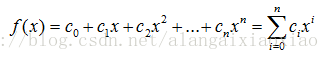
①ci的值決定了反饋線的連接狀態；

②在上式和后面的公式中都將“”簡寫為“+”；

③式中xi本身并無實際意義，它僅指明其系數是ci的值。

④特征方程f(x)決定了一個線性反饋移存器的結構，從而決定了它產生的序列的構造和周期。

4.本原多項式

使一個線性反饋移存器產生最長周期序列的充分必要條件是其特征方程f(x)為本原多項式,最長周期為2^n-1。

本原多項式是指滿足下列條件的多項式：

①是既約的，即不能分解因子的；

② 可以整除(x^m + 1)，m = 2^n – 1；即是( x^m + 1 )的一個因子；

③ 除不盡( x^q+ 1 )，q < m。

常用本原多項式：(最高位和最低位系數必須都是1)，同時n也是多項式最高項的次數和LFSR寄存器個數；

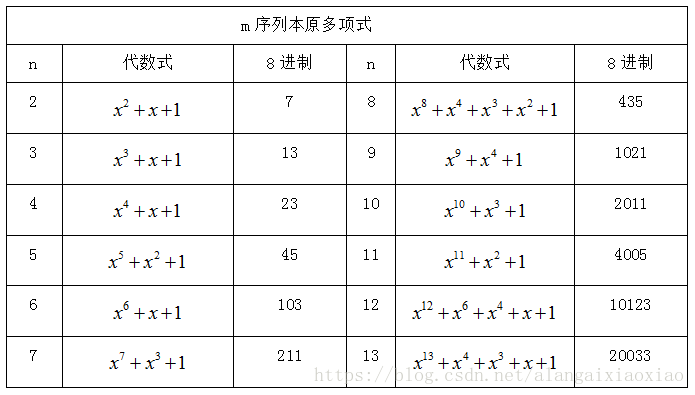
示例如下：

表示上式中僅x0, x1,和x4的系數c0 = c1 = c4 = 1，而其余系數c2 = c3 = 0，則：

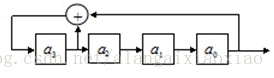
n=4,m=2^4-1 g(x)=x^4+x+1;

在最長線性序列移位寄存型計數器中，存在一個“00000”，該狀態構成死循環，這會使電路不具有自啟動功能，為了解決這個問題，可在反饋方程中加全0校正項 （~Q1）&（~Q2）…..

例如：

此時的反饋函數F= Q1^Q4+（~Q0）&（~Q1）&（~Q2）&（~Q3）&（~Q4）;

相應地verilog代碼如下:

module m_sequence(

input I_clk,

input I_rst_p,

input en,

input [3:0] D_init,

output dout

)

wire F;

reg [3:0] m_reg;

always@(posedge I_clk)

if(I_rst_p)

m_reg <= 4'b0;

else if(en)

m_reg <= D_init;

else

m_reg <= {m_reg[2:0],F };

assign F=(m_reg[1]^m_reg[4])|(~(|m_reg)) ;

assign dout = m_reg[3];

endmoduel

審核編輯：湯梓紅