在實際的工程應用中，工程結構往往并不是單自由度系統。不僅如此，阻尼器自身也有極大的可能并不是單自由度系統，下面我們就用一個工程案例來進行分析。

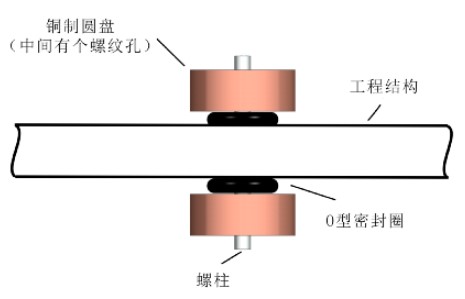
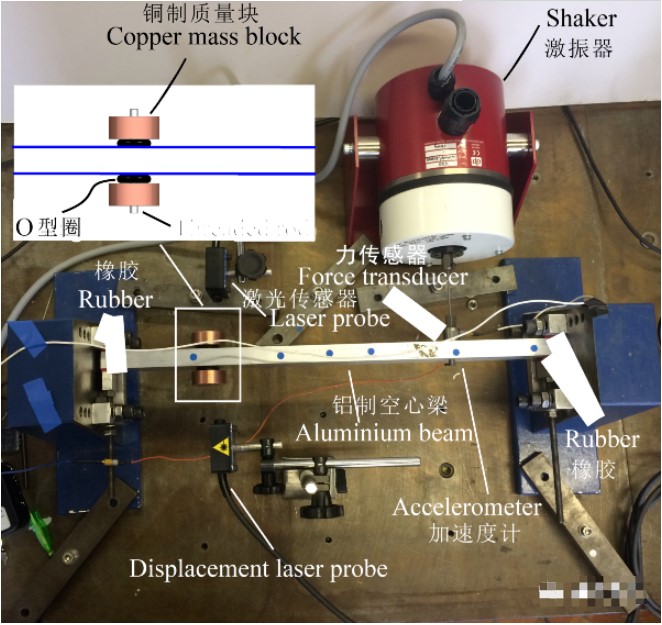
一個很簡單的調諧質量阻尼器可以如上圖所述。該減振器使用兩個相同的銅質圓盤和彈性O型環，機械地連接到工程結構上。在這些圓盤的中間有兩個螺紋孔，通過螺柱，這兩個銅質圓盤被夾在主結構上。該螺柱穿過工程結構而不接觸該結構。O型環的靜態壓縮可以通過螺紋桿進行調整。使用這個阻尼器的結構，在調整O型密封圈靜態形變的同時，將接觸面的摩擦降到最低。與此同時，在這種設計中，O型圈不僅為系統提供了剛度和阻尼，而且它們還隔離了作為TMD質量一部分的螺紋桿。因此，在設計中沒有多余的部件，可以有效地節省成本以及提高可靠性。此外，這個阻尼器的剛度是可調的。隨著不同的O型圈的靜態壓縮，可以獲得不同的阻尼器的動剛度。不僅如此，這個阻尼器的剛度和阻尼也是可以預測的。因此，設計者就能夠遵循一種非常簡單的方法來設計這個阻尼器，即：

根據所需的TMD質量來選擇螺紋桿和圓盤的材料和質量。

選擇O型環的材料、直徑和線徑，以達到理想的阻尼和剛度。

靜態壓縮的最終調整，以達到最優化的共振頻率。

1、調諧質量阻尼器的工作模態

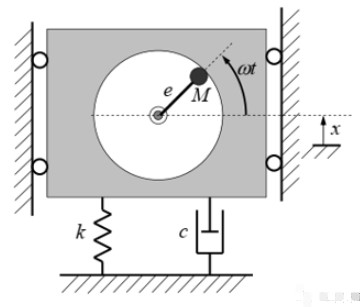
在經典的調諧質量阻尼器的設計理論之中，往往只考慮其一個自由度。但對于實際的結構，它的工作模態通常更加復雜。對于我們所說的例子，這個阻尼器可以有壓縮（compressive）、搖晃（rocking）和剪切（shear）等不同的工作模態。典型的模態形狀在下圖顯示：

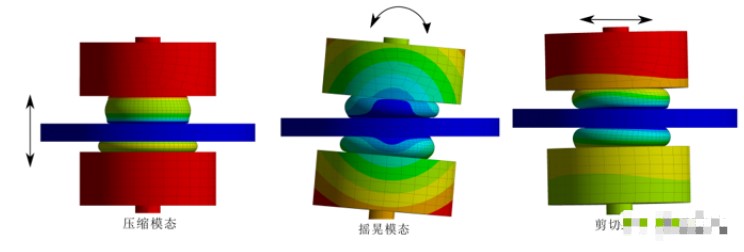
在這個阻尼器中，一般考慮的設計是壓縮模態，因為其他模態可能會對主機結構產生意想不到的影響。它可能對于主體結構產生意外，造成有利或者有害的影響。例如，工程結構的橫向振動將激發另外兩個阻尼器模態（搖擺和剪切），它們會與工程結構的運動產生相互作用。這與理想的阻尼器設計原理是截然不同的。然而，這些額外的模態也可以提供有益的減振效果。判斷這些額外的模態是否有效主要還是取決于工程結構的模態。

傳統的調諧質量阻尼器一個重要的弊端是它只能在有限的頻率范圍內工作。對于這個實際的調諧質量阻尼器，每一個不同的模態將會對應一個不同的頻率。這直接導致了這個阻尼器的可用工作頻率變得更大。不僅如此，當我們壓縮O型圈，從而改變這個彈性元件的靜態壓縮量時，O型圈的剛度可以變化，通過這個操作，這個阻尼器的固有頻率也可以改變。在O型圈不同的靜態壓縮量時，這個阻尼器的固有頻率可以如下圖所示。

我們可以看到，隨著靜態壓縮量的增加，這種阻尼器的共振頻率將會大大提高。隨著O型圈的靜態壓縮量的增加，它的剛度對于不同方向的幾何非線性造成了不同的固有頻率的增加量。搖擺模態對初始壓縮的敏感度較高，這是因為在這種模式中，密封圈的變形不僅增加了其與金屬表面的接觸面積，還使O型圈進一步遠離阻尼器的中心線，從而增加其對搖擺的阻力。對于其他模式，O型圈相對于阻尼器中心線的位置并不重要。因此，對于搖擺模態，我們可以觀察到更大的剛性增強。

2、O型圈的剛度和阻尼變化曲線

在這個設計之中，O型圈是被作為阻尼器的剛度和阻尼元件。為了建立阻尼器的設計曲線（master curve），O型圈的剛度和阻尼的理論或者有限元模型需要被建立，然而，這里面包含相對比較復雜的數學模型。這里，我們只是將對O型圈與靜態壓縮量相關的阻尼和剛度變化的實驗結果顯示了出來：

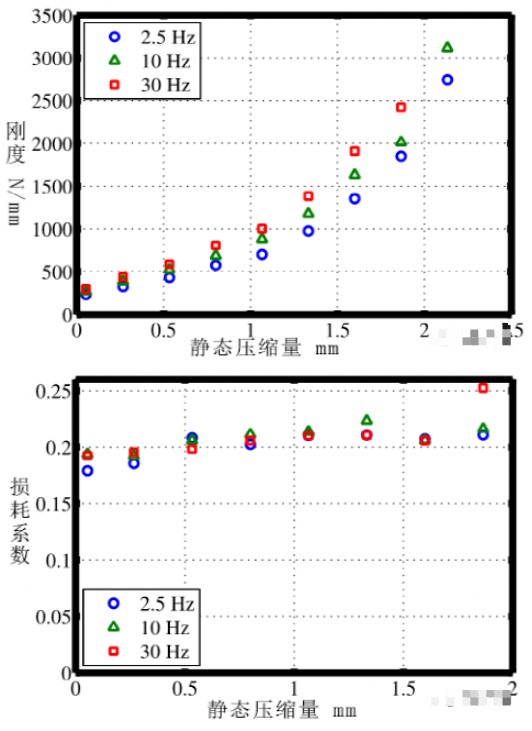
我們可以看到，O型圈的剛度隨著靜態壓縮量呈多項式函數增長，而阻尼基本保持一致。這就為我們設計作用于寬頻的調諧質量阻尼器提供了基礎。

3、調諧質量阻尼器設計曲線

我們所設計的這個調諧質量阻尼器在選定的頻率范圍內，實質上有兩個工作模態，阻尼器的拉伸壓縮模態與搖擺模態。在設計時，我們在考慮最優化的設計參數時，也需要同時考慮這兩個模態。在初始設計時，可以只考慮拉升壓縮模態，用于選定阻尼器的質量參數。在選定阻尼器的質量時，以下幾個原則必須考慮到：

阻尼器中質量塊在豎直方向的局部模態（local mode）將不會影響到整個阻尼器的工作模態。

利用簡單的螺柱連接，阻尼器的質量塊需要對于O型圈施加均一的靜態應變。

考慮到O型圈的剛度范圍相對固定，阻尼器的質量塊選擇需要滿足其設計頻率。

下圖中就顯示了一個典型的調諧質量阻尼器設計曲線，它總和O型圈的靜態壓縮量有關。圖中藍色的實線代表阻尼器在拉伸壓縮模態時的工作頻率，綠色的虛線代表了其在搖擺模態時的工作頻率。橫向虛線代表了主結構的第一階和第二階的彎曲模態。縱向的點劃線代表著若干選定的O型圈靜態壓縮量。

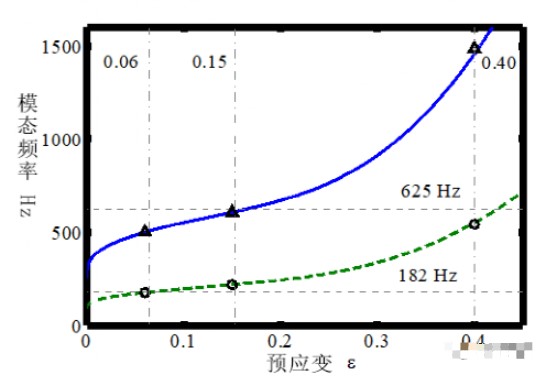
傳統的阻尼器設計理論總是認為質量比對于阻尼器的調制頻率有很大的影響。但實際上，這些阻尼器的設計理論往往都在考慮數學上的最優化解。在工程實踐上，一個更為簡化的方法就是假設阻尼器的工作模態頻率和主結構的自然頻率相等。這其實包含了以下幾個假設：（1）阻尼器的質量通常遠小于主結構的質量，它對于主結構的模態影響基本可以忽略不計；（2）對于調諧質量阻尼器，由于阻尼的存在，其對于阻尼器的模態頻率敏感度有限。所以，為了便于設計，我們將阻尼器設計的模態頻率假設為主結構的固有頻率。

在上圖中，我們可以看到當靜態壓縮量約為O型圈直徑的6%、15%和40%時，結構和阻尼器之間會發生相互作用。對于一個小型O型圈而言，最小靜態壓縮量為其直徑的6%左右。當靜態壓縮量小于6% 時，橡膠與金屬的靜摩擦力不足以使O型圈保持在其設計的位置。在這個壓縮量時，阻尼器搖擺模態將作用于主結構的第一階彎曲模態。當預壓縮量增加到15%時，搖擺模態仍將對于第一階彎曲模態有效，與此同時，拉伸壓縮模態也將作用于第二階彎曲模態。在O型圈40%的靜態壓縮量下，阻尼器搖擺模態則將減低主結構的第二階彎曲模態的振動。

4、實驗驗證

實驗驗證的模型如下圖所示。這個可調調諧質量阻尼器被安裝在一個空心梁上。阻尼器被安裝在梁的第二階彎曲模態的反節點位置上（anti-node）。值得注意的是，兩個激光傳感器是用于判斷O型圈的靜態壓縮量。

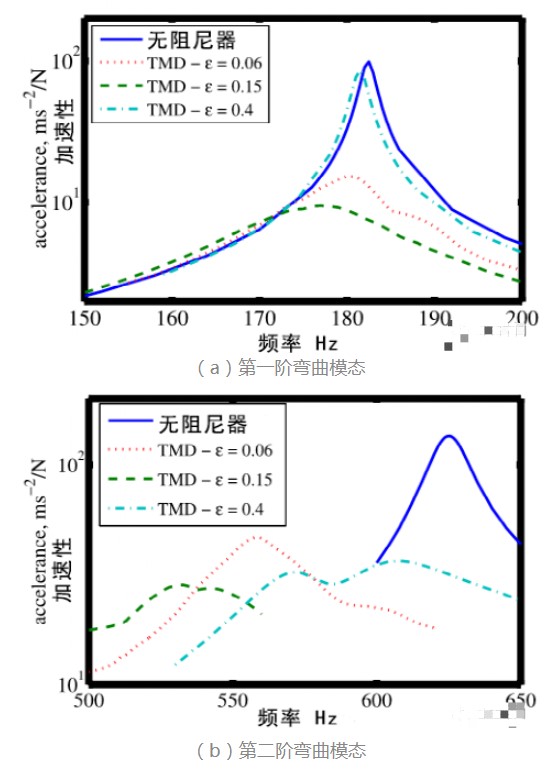
當阻尼器調整至不同的工作狀態時，下面兩張圖片顯示了空心梁上的加速度頻響函數（accelerometer frequency response）。當O型圈受到6%的靜態壓縮率時，空心梁對于第一階彎曲模態（約185Hz）的橫向振動被抑制了10倍。隨著靜態壓縮量的增加，阻尼器對于第一階彎曲模態的結構震動控制變得不那么有效。當靜態壓縮率為40%時，600Hz附近的振動水平（與主結構的第二階彎曲模態相關）幾乎降低了8倍。最后，在O型圈15%的靜態壓縮率下，這兩個結構共振都得到了有效的抑制。這些結果證實我們所使用的設計方法的可靠性。

5、結語

在這篇文章中，我們介紹了一種實際的調諧質量阻尼器的設計準則。它的設計方法源于基本的阻尼器理論。但是在實踐中，我們需要考慮更多的變量，以便于我們的阻尼器更有效地工作在我們所需要的主結構模態。

審核編輯：劉清