混頻器是一種特殊類型的電子電路，它結合了兩個信號（周期性重復的波形）。混音器在音頻和射頻系統中得到了廣泛應用，很少用作簡單的模擬“計算機”。有兩種類型的模擬音頻混音器——加法混音器和乘法混音器。

1. 添加劑混合器

就像它們的名字所暗示的那樣，加法混頻器只是簡單地將兩個信號的值在任何時刻相加，從而在輸出端產生一個連續波形，該波形是各個波形值的總和。

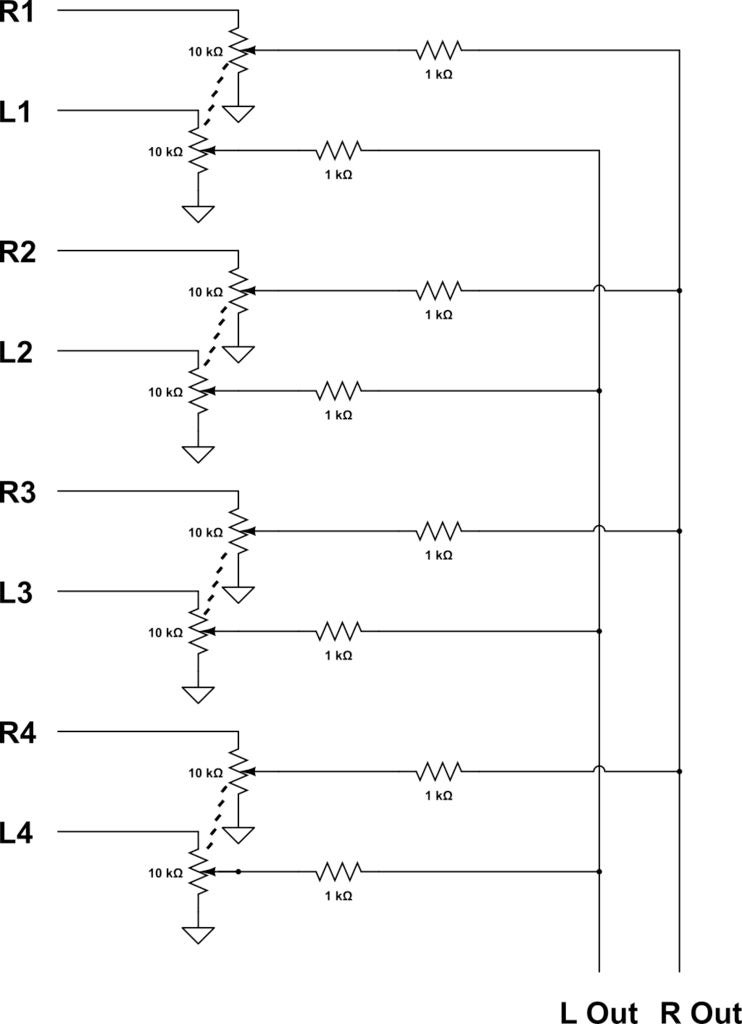
最簡單的加法混頻器只是兩個信號源以下列方式連接到兩個電阻器：

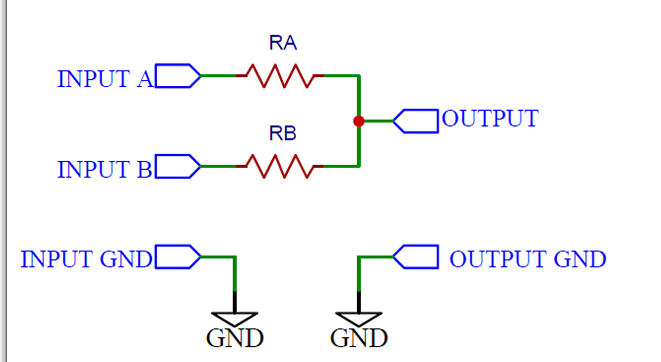
電阻器防止信號源相互干擾，加法發生在公共節點，而不是信號源本身。這種方法的優點在于可以根據各個電阻值進行加權求和。

從數學上講，

z = Ax + By

其中“z”是輸出信號，“x”和“y”是輸入信號，“A”和“B”是比例比例因子，即相對于彼此的電阻值。

例如，如果其中一個電阻值為 10K，另一個為 5K，則 A 和 B 分別變為 2 和 1，因為 10K 是 5K 的兩倍。

當然，使用此音頻混音器可以將兩個以上的信號組合在一起。

構建一個簡單的添加劑混合器

所需零件：

1. 2x 10K 電阻

2. 1x 3.3K 電阻

3.一個雙通道信號源

電路原理圖：

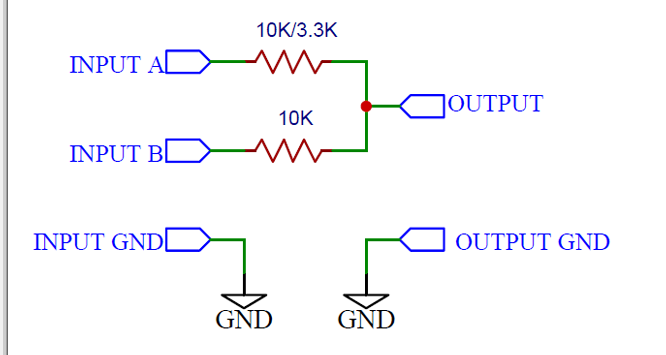
使用兩個 10K 電阻，輸出只是輸入信號的總和。A 和 B 都是統一的，因為兩個縮放電阻器是相同的。

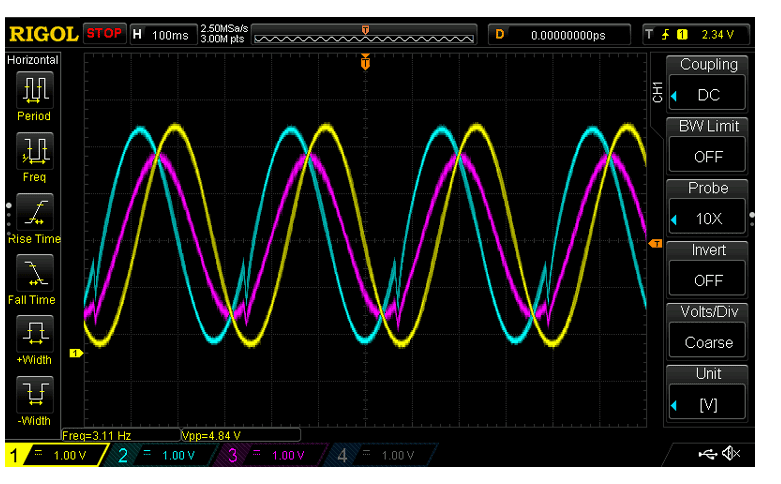
黃色和藍色波形是輸入，粉色波形是輸出。

當我們用 3.3K 電阻器替換 10K 電阻器中的一個時，比例因子變為 3 和 1，并且一個信號的三分之一被添加到第二個。

數學方程為：

z = x + 3y

下圖顯示了結果輸出波形為粉紅色，輸入為黃色和藍色。

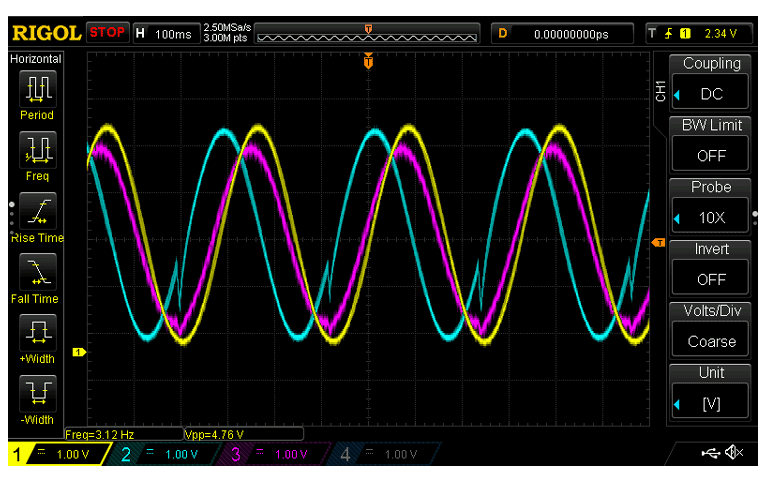
添加劑混合器的應用

像這樣的簡單混音器最引人注目的業余愛好者使用耳機均衡器或“單聲道到立體聲”轉換器的形式，它使用兩個（通常）10K 將左右聲道從 3.5 毫米立體聲插孔轉換為單聲道電阻器。

2.乘法混合器

乘法混頻器更有趣一些——它們將兩個（或者更多，但這很困難）輸入信號相乘，乘積就是輸出信號。

加法很簡單，但是我們如何進行電子乘法呢？

我們可以在這里應用另一個小數學技巧，稱為對數。

對數基本上是在問一個問題——必須將給定的基數提高到多少才能給出結果？

換句話說，

2 x = 8， x = ？

就對數而言，這可以寫成：

日志2 x = 8

用公共底的指數來寫數字使我們能夠使用另一個基本的數學屬性：

a x xa y = a x+y

將兩個指數乘以公共底數相當于將指數相加，然后將底數提高到該次方。

這意味著，如果我們對兩個信號應用對數，將它們加在一起然后“取”一個反對數就相當于將它們相乘！

電路實現可能會有點復雜。

在這里，我們將討論一個相當簡單的電路，稱為吉爾伯特單元混頻器。

吉爾伯特細胞混合器

下圖顯示了吉爾伯特單元混頻器電路。

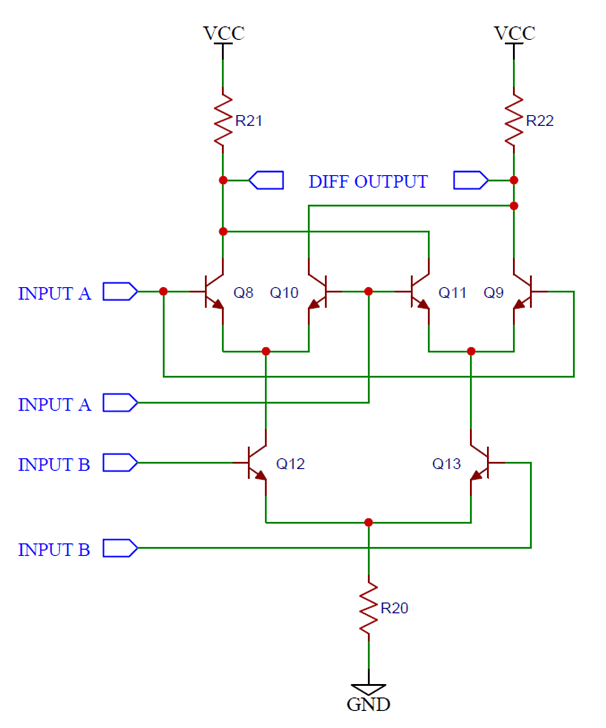
該電路一開始可能看起來很嚇人，但就像所有復雜的電路一樣，這個電路可以分解成更簡單的功能塊。

晶體管對 Q8/Q10、Q11/Q9 和 Q12/Q13 形成單獨的差分放大器。

差分放大器只是放大兩個晶體管的差分輸入電壓。考慮下圖所示的簡單電路。

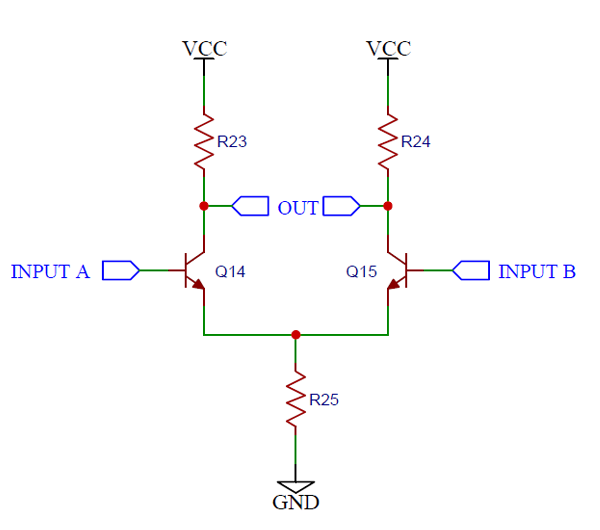
輸入為差分形式，位于晶體管 Q14 和 Q15 的基極之間。基極電壓相同，集電極電流也相同，R23 和 R24 兩端的電壓相同，因此輸出差分電壓為零。如果基極電壓不同，則集電極電流不同，從而在兩個電阻器上設置不同的電壓。由于晶體管的作用，輸出擺幅大于輸入擺幅。

從中得出的結論是，放大器的增益取決于尾電流，即兩個集電極電流的總和。尾電流越大，增益越大。

在上面所示的吉爾伯特單元混頻器電路中，頂部的兩個差分放大器（由 Q8/Q10 和 Q11/Q9 組成）具有交叉連接的輸出和一組公共負載。

當兩個放大器的尾電流相同且差分輸入A為0時，電阻兩端的電壓相同，沒有輸出。當輸入 A 具有較小的差分電壓時也是如此，由于尾電流相同，因此交叉連接抵消了整體輸出。

只有當兩個尾電流不同時，輸出電壓才是尾電流之差的函數。

取決于哪個尾電流更大或更小，增益可以是正的或負的（相對于輸入信號），即反相或非反相。

尾電流的差異是使用由晶體管 Q12/Q13 形成的另一個差分放大器產生的。

總體結果是輸出差分擺幅與輸入 A 和 B 的差分擺幅的乘積成正比。

構建吉爾伯特細胞混合器

所需零件：

1. 3x 3.3K 電阻

2. 6x NPN晶體管（2N2222、BC547等）

兩個相移正弦波被饋入輸入（由黃色和藍色跡線顯示），輸出在下圖中以粉紅色顯示，與示波器的數學乘法函數相比，其輸出為紫色跡線。

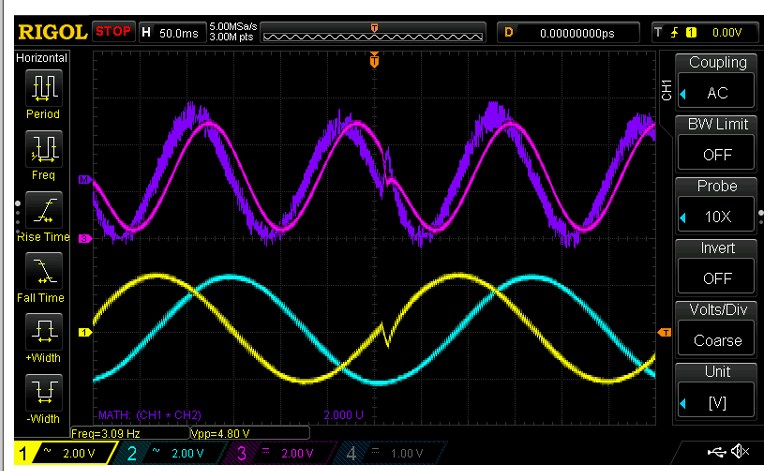
由于示波器進行“實時”乘法，因此輸入必須是交流耦合的，以便它也計算負峰值，因為實際混頻器的輸入是直流耦合的，它可以處理兩個極性的乘法。

混頻器輸出和示波器軌跡之間也存在細微的相位差，因為在現實生活中必須考慮傳播延遲等因素。

乘法混頻器的應用

乘法混頻器的最大用途是在射頻電路中，通過將高頻波形與中頻波形混合來解調。

像這樣的吉爾伯特細胞是一個四象限乘法器，這意味著兩個極性的乘法都是可能的，遵循簡單的規則：

A x B = AB

-A x B = -AB

A x -B = -AB

-A x -B = AB

Arduino正弦波發生器

該項目使用的所有波形都是使用 Arduino 生成的。我們之前已經詳細解釋了Arduino函數發生器電路。

電路原理圖：

12

代碼說明：

設置部分使用正弦函數的值創建兩個查找表，縮放為從 0 到 255 的整數，其中一個相移 90 度。

循環部分只是將查找表中存儲的值寫入 PWM 定時器。PWM 引腳 11 和 3 的輸出可以經過低通濾波以獲得近乎完美的正弦波。這是 DDS 或直接數字合成的一個很好的例子。

產生的正弦波具有非常低的頻率，受 PWM 頻率的限制。這可以通過一些低級寄存器魔法來解決。正弦波發生器的完整 Arduino 代碼如下：

#define pinOne 11
#define pinTwo 3
#定義圓周率 3.14
浮動階段 = 0;
int 結果，resultTwo，sineValuesOne，sineValuesTwo，i，n；
無效設置（）
{
pinMode（pinOne，輸出）；
pinMode（pinTwo，輸入）；
序列號.開始（115200）；
for(相位 = 0, i = 0; 相位 <= (2*pi); 相位 = 相位 + 0.1, i++)
{
結果 = (50 * (2.5 + (2.5 * sin(相位))));
sineValuesOne[i] = 結果；
resultTwo = (50 * (2.5 + (2.5 * sin(相位 - (pi*0.5)))));
sineValuesTwo[i] = 結果二；
}
n = 我;
}
無效循環（）
{
for(i = 0; i <= n; i++)
{
類比寫入（pinOne，sineValuesOne[i]）；
類比寫入（pinTwo，sineValuesTwo[i]）；
延遲（5）；
}
}

結論

混頻器是兩個輸入相加或相乘的電子電路。它們廣泛用于音頻、射頻，偶爾也用作模擬計算機的元件。