簡述數據結構棧
棧是一種線性表,其限制只能在表尾進行插入或刪除操作。由于該特性又稱為后進先出的線性表。
簡述數據結構隊列
隊列是一種先進先出的線性表。其限制只能在線性表的一端進行插入,而在另一端刪除元素。
簡述二叉樹
二叉樹是n個有限元素的集合,該集合或者為空、或者由一個稱為根(root)的元素及兩個不相交的、被分別稱為左子樹和右子樹的二叉樹組成。
簡述滿二叉樹
一個二叉樹,如果每一個層的結點數都達到最大值,則這個二叉樹就是滿二叉樹。
簡述完全二叉樹
一棵深度為k的有n個結點的二叉樹,對樹中的結點按從上至下、從左到右的順序進行編號,如果編號為i(1≤i≤n)的結點與滿二叉樹中編號為i的結點在二叉樹中的位置相同,則這棵二叉樹稱為完全二叉樹。
簡述二叉樹的前中后序遍歷算法
前序遍歷:若二叉樹為空樹,則執行空邏輯,否則:
訪問根節點
遞歸前序遍歷左子樹
遞歸前序遍歷右子樹
中序遍歷:若二叉樹為空樹,則執行空邏輯,否則:
遞歸中序遍歷左子樹
訪問根節點
遞歸中序遍歷右子樹
后序遍歷:若二叉樹為空樹,則執行空邏輯,否則:
遞歸后序遍歷左子樹
遞歸后序遍歷右子樹
訪問根節點
簡述解決Hash沖突的方法
開放定址法:當發生哈希沖突時,如果哈希表未被裝滿,那么可以把這個值存放到沖突位置中的下一個空位置中去
鏈地址法:對相同的哈希地址,設置一個單鏈表,單鏈表內放的都是哈希沖突元素。
簡述AVL樹
AVL樹是一種改進版的搜索二叉樹,其引入平衡因子(左子支高度與右子支高度之差的絕對值),通過旋轉使其盡量保持平衡。任何一個節點的左子支高度與右子支高度之差的絕對值不超過1。
簡述紅黑樹
紅黑樹本身是有2-3樹發展而來,紅黑樹是保持黑平衡的二叉樹,其查找會比AVL樹慢一點,添加和刪除元素會比AVL樹快一點。增刪改查統計性能上講,紅黑樹更優。紅黑樹主要特征是在每個節點上增加一個屬性表示節點顏色,可以紅色或黑色。紅黑樹和 AVL 樹類似,都是在進行插入和刪除時通過旋轉保持自身平衡,從而獲得較高的查找性能。紅黑樹保證從根節點到葉尾的最長路徑不超過最短路徑的 2 倍,所以最差時間復雜度是 O(logn)。紅黑樹通過重新著色和左右旋轉,更加高效地完成了插入和刪除之后的自平衡調整。
簡述穩定排序和非穩定排序的區別
穩定排序:排序前后兩個相等的數相對位置不變,則算法穩定非穩定排序:排序前后兩個相等的數相對位置發生了變化,則算法不穩定
常見的穩定排序算法有哪些
插入排序、冒泡排序、歸并排序
常見的不穩定排序算法有哪些
希爾排序、直接選擇排序、堆排序、快速排序
簡述插入排序
插入排序:每一趟將一個待排序記錄按其關鍵字的大小插入到已排好序的一組記錄的適當位置上,直到所有待排序記錄全部插入為止。
排序算法穩定。時間復雜度 O(n2),空間復雜度 O(1)。
簡述希爾排序
希爾排序:把記錄按下標的一定增量分組,對每組進行直接插入排序,每次排序后減小增量,當增量減至 1 時排序完畢。
排序算法不穩定。時間復雜度 O(nlogn),空間復雜度 O(1)。
簡述直接選擇排序
直接選擇排序:每次在未排序序列中找到最小元素,和未排序序列的第一個元素交換位置,再在剩余未排序序列中重復該操作直到所有元素排序完畢。
排序算法不穩定。時間復雜度 O(n2),空間復雜度 O(1)。
簡述堆排序
堆排序:將待排序數組看作一個樹狀數組,建立一個二叉樹堆。通過對這種數據結構進行每個元素的插入,完成排序工作。
排序算法不穩定,時間復雜度 O(nlogn),空間復雜度 O(1)。
簡述冒泡排序
冒泡排序:比較相鄰的元素,如果第一個比第二個大就進行交換,對每一對相鄰元素做同樣的工作。
排序算法穩定,時間復雜度 O(n2),空間復雜度 O(1)。
簡述快速排序
快速排序:隨機選擇一個基準元素,通過一趟排序將要排序的數據分割成獨立的兩部分,一部分全部小于等于基準元素,一部分全部大于等于基準元素,再按此方法遞歸對這兩部分數據進行快速排序。
排序算法不穩定,時間復雜度 O(nlogn),空間復雜度 O(logn)。
簡述歸并排序
歸并排序:將待排序序列分成兩部分,然后對兩部分分別遞歸排序,最后進行合并。排序算法穩定,時間復雜度都為 O(nlogn),空間復雜度為 O(n)。
簡述圖
圖是由頂點集合和頂點之間的邊集合組成的一種數據結構,分為有向圖和無向圖。
有向圖:邊具有方向性
無向圖:邊不具有方向性
簡述鄰接矩陣
用一個二維數組存放圖頂點間關系的數據,這個二維數組稱為鄰接矩陣。對于無向圖,鄰接矩陣是對稱矩陣
簡述鄰接表
鄰接表是通過鏈表表示圖連接關系的一種方。對于表頭結點所對應的頂點存在相鄰頂點,則把相鄰頂點依次存放于表頭結點所指向的單向鏈表中。
簡述圖的深度優先搜索DFS
將圖中每個頂點的訪問標志設為 FALSE, 之后搜索圖中每個頂點,如果未被訪問,則以該頂點V0為起始點出發,訪問此頂點,然后依次從V0的各個未被訪問的鄰接點出發深度優先搜索遍歷圖,直至圖中所有和V0有路徑相通的頂點都被訪問到。
簡述圖的廣度優先搜索
從圖中的某個頂點V0出發,并在訪問此頂點之后依次訪問V0的所有未被訪問過的鄰接點,之后按這些頂點被訪問的先后次序依次訪問它們的鄰接點,直至圖中所有和V0有路徑相通的頂點都被訪問到。
簡述最小生成樹和其對應的算法
對于有 n 個結點的原圖,生成原圖的極小連通子圖,其包含原圖中的所有 n 個結點,并且有保持圖連通的最少的邊。
普里姆算法:取圖中任意一個頂點 v 作為生成樹的根,之后往生成樹上添加新的頂點 w。在添加的頂點 w 和已經在生成樹上的頂點v 之間必定存在一條邊,并且該邊的權值在所有連通頂點 v 和 w 之間的邊中取值最小。之后繼續往生成樹上添加頂點,直至生成樹上含有 n-1 個頂點為止。
克魯斯卡爾算法:先構造一個只含 n 個頂點的子圖 SG,然后從權值最小的邊開始,若它的添加不使 SG 中產生回路,則在 SG 上加上這條邊,如此重復,直至加上 n-1 條邊為止。
簡述最短路徑算法
Dijkstral算法為求解一個點到其余各點最小路徑的方法,其算法為:
假設我們求解的是頂點v到其余各個點的最短距離。n次循環至n個頂點全部遍歷:
從權值數組中找到權值最小的,標記該邊端點k
打印該路徑及權值
如果存在經過頂點k到頂點i的邊比v->i的權值小
更新權值數組及對應路徑
簡述堆
堆是一種完全二叉樹形式,其可分為最大值堆和最小值堆。
最大值堆:子節點均小于父節點,根節點是樹中最大的節點。
最小值堆:子節點均大于父節點,根節點是樹中最小的節點。
簡述set
Set是一種集合。集合中的對象不按特定的方式排序,并且沒有重復對象。
說一下對于樹的理解
數據結構樹是一種由有限節點組成的層次關系的集合。其特點如下:
每個節點有零個或多個子節點;
只有一個節點沒有父節點,該節點稱為根節點;
除根節點外,每個節點有且只有一個父節點;
簡述二叉查找樹
二叉查找樹的左子樹若不為空,則左子樹上所有結點的值均小于它的根結點的值;
二叉查找樹的右子樹若不為空,則右子樹上所有結點的值均大于它的根結點的值;
二叉查找樹的左、右子樹也分別為二叉查找樹;
沒有鍵值相等的結點。
審核編輯 :李倩
-
算法
+關注
關注
23文章
4625瀏覽量
93143 -
數據結構
+關注
關注
3文章
573瀏覽量
40184 -
二叉樹
+關注
關注
0文章
74瀏覽量
12358
原文標題:數據結構與算法八股文背誦版V0.3
文章出處:【微信號:TheAlgorithm,微信公眾號:算法與數據結構】歡迎添加關注!文章轉載請注明出處。
發布評論請先 登錄
相關推薦
DDC264配置寄存器數據寫入和320 DCLK時鐘脈沖后的回讀數據結構是什么?
視覺軟件HALCON的數據結構
U盤存儲并聯,算法交互輸出
嵌入式常用數據結構有哪些
簡述基本與非門sr鎖存器的結構及工作原理
神經網絡算法的結構有哪些類型
簡述數控機床對結構與性能的要求
解析嵌入式編程8種常用的數據結構
STM32的ADC項目應用,用什么算法濾波和穩定數據抖動?
TASKING編譯器是否可以將數據結構設置為 \"打包\"?
矢量與柵格數據結構各有什么特征
Redis流與Kafka相比如何?
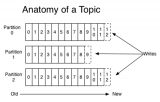




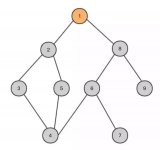
 數據結構與算法簡述
數據結構與算法簡述











評論