最近跟一個同事聊了聊天，他說一直用的位置式PID，從來沒在具體項目中用過增量式PID，感覺兩者沒啥區別呀？

于是跟他討論了一番，不由得讓人深思~

1

“萬能”的PID

PID是一種非常經典的控制類算法，憑著它的簡單易用在工程上得到了廣泛的應用，并且影響力也是極高，那為什么說其簡單易用呢？

可以說只要你對PID的主要的參數對系統的影響理解得足夠好，完全可以通過手動試湊的方式來獲得一套合適的PID參考，所以對一些非控制類的工程師應用起來也是非常友好的。

當然還有一個非常重要的原因，PID算法對大部分系統穩定性、魯棒性以及可靠性都非常的高，有調試PID控制算法經驗的朋友應該都有類似的感覺，即便根據經驗隨便給系統一套參數都可以到達一個不錯的控制效果。

所以在很多人眼里這算法就是"萬能的"，適應的場景也非常的廣泛，然而自古有一種規律"熊掌和魚不可以兼得"，PID算法雖然適應性非常廣泛，對于處理一些特定的應用場景，或許其并不會最優的解決辦法。

基于大家在實際應用中各種各樣的需求，曾經一個發展涌現了非常的PID的變種，也就是對PID算法在特定的應用場景進行優化、或者與其他一些控制方法進行結合，以便達到相應控制場景下的不錯控制效果，比如微分先行PID、PID與智能控制的算法的結合等等。

當然如果PID算法實在無法滿足需求了，那也不能勉強，就只能考慮尋找另外更為匹配的控制策略，比如現在非常流行的自抗擾控制技術等等。

2

PID的理解

PID算法主要就是三項，比例（P）-積分（I）-微分（D），在連續的時間域內的表達式如下:

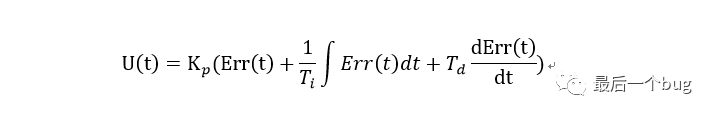
從上面的公式可以看出PID算法是一個非常純粹的數學表達式，既然是數學表達式那必然可以通過數學的方式進行分析，拉式變換一下，獲得傳遞函數，然后采用控制理論分析方法，結合被控對象分析其對動態系統的穩定性、準確性以及快速性進行分析，從而達到性能上的最優解，這個控制系統的設計過程不是本文重點，暫時就不進行展開了。

還記得最開始了解這個算法的時候，有一句話非常相信的彰顯其魅力所在：P-I-D分別代表著當前、過去和未來。P對當前誤差的抑制作用；I對歷史誤差的累積控制，以便消除靜態誤差；D根據誤差的變化率進行補償，從表達式也非常容易從根本上理解這幾句話。

3

數字PID

在前面跟大家簡單描述了連續域內的PID算法表達式，而連續域中該算法需要通過相應的模擬電路來進行實現，特別是一些沒有數字芯片的嵌入式系統是經常可見的。

但隨著數字系統的應用，特別是單片機系統，數字PID更加得到廣泛的應用，被大部分人所熟知的兩種數字PID，分別是位置式PID和增量式PID。

大部分的教材都會描述著兩種形式的數字PID，然而這些教材一上來就介紹位置式PID與歷史狀態相關，過去會對現在的控制輸出產生影響，而增量式PID僅僅只與最近的幾次誤差數據相關。

如下是位置式PID表達式:

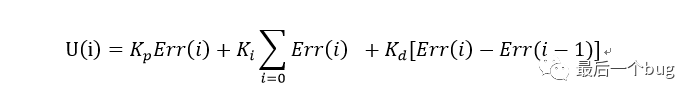
而增量式PID的形式則可以通過位置式進行如下表達式處理得到:

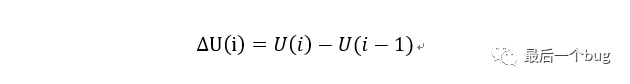
如下便可以得到增量式的表達式：

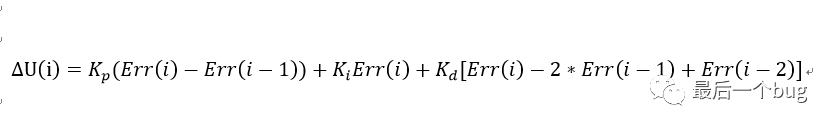
這樣看來增量式PID只與最近的兩次誤差有關系，不會存在累積誤差的問題，說來增量式PID必然是更好的，那為何還要介紹位置式PID呢？

也有伙計在自己的程序中使用增量式PID的表達式，畢竟增量式PID其輸出僅僅只是控制量的增量，最后還是需要把輸出量進行累積，這與位置式根本沒啥區別。

于是很多初學者，甚至一些用PID多年的工程師對此都抱有一絲疑問。

其實這兩種數字PID的應用場景是有區別的，增量式PID控制輸出的僅僅只是控制量的增量，其主要是應用在執行機構帶有積分部件的被控對象，而位置式PID其輸出的是實際的控制量，則用于不帶積分環節的執行機構。

當然如果在一些不帶積分環節的執行結構系統中你執意要使用增量PID的形式也無傷大雅，只是最后用數字積分進行處理后輸出，其與位置式PID式沒有差異，增量式PID的優勢并沒有展現，因為真正單獨使用增量式PID的執行機構的積分環節是連續的，這是數字離散的方式無法比擬的。

審核編輯 ：李倩