網格劃分是進行有限元分析和計算的前提，也是最費時間最費精力的一項前處理技術，網格劃分的質量對有限元計算的精度和計算效率都有著最為直接的影響，對于大變形的情況甚至影響到解的收斂性。目前比較通用的分網軟件主要有Hypermesh、ANSA、ANSYS、MARC等，本文就復雜模型的分網技術進行簡明的闡述。

自由網格劃分

自由網格劃分是自動化程度最高的網格劃分技術之一，它在面上（平面、曲面）可以自動生成三角形或四邊形網格，在體上自動生成四面體網格。通常情況下，可利用Hypermesh的2D面板的automesh來對面和網格單元自動劃分。

對于復雜幾何模型而言，自動分網方法省時省力，但缺點是單元數量甚至會出現單元不能達到預想的效果，如在某些地方需要較少單元，而在另外的地方需要更多的單元時，通常不容易控制。因此需要對面進行一些幾何分塊處理，以得到符合分網工作者的意愿的具有較高計算效率的網格。

對于三維復雜模型只能生成四面體單元，分網效率極高，只要設置相關參數就等得到較好的網格，但是網格數量取決于幾何模型的最小特征，網格數量通常非常大，因此為了獲得更高的計算效率的有限元網格，通常要對幾何模型進行一些處理，和二維情況類似，可以進行分塊處理，如進行局部細分。

映射網格劃分

映射網格劃分是對規整模型的一種規整網格劃分方法，其原始概念是：對于面，只能是四邊形面，網格劃分數需在對邊上保持一致，形成的單元全部為四邊形；對于體，只能是六面體，對應線和面的網格劃分數保持一致；形成的單元全部為六面體。

目前大多數分網軟件對這些條件有了很大的放寬，包括：

面可以是三角形、四邊形、或其它任意多邊形。

面上對邊的網格劃分數可以不同，但有一些限制條件。

面上可以形成全三角形的映射網格。

體可以是四面體、五面體、六面體或其它任意多面體。

體上對應線和面的網格劃分數可以不同，但有一些限制條件。

對于三維復雜幾何模型而言，通常的做法是利用線面切割功能，將其切割成一系列四、五或六面體，然后對這些切割好的體進行映射網格劃分。當然，這種純粹的映射劃分方式比較煩瑣，需要的時間和精力較多，但能保證較高的網格質量。

拖拉、掃略網格劃分

對于由面經過拖拉、旋轉、偏移等方式生成的復雜三維實體而言，可先在原始面上生成殼單元形式的面網格，然后在生成體的同時自動形成三維實體網格。對于已經形成好了的三維復雜實體，如果其在某個方向上的拓撲形式始終保持一致，則可用掃略網格劃分功能來劃分網格；這兩種方式形成的單元幾乎都是六面體單元。

在Hypermesh三維面板中的solidmap功能，可以實現幾種形式的拖拉和掃略，如從單元到面，從面到面，可以選擇的拉伸方式也多種，根據具體的情況進行靈活選擇，通常，采用掃略方式形成網格是一種非常好的方式，對于復雜幾何實體，經過一些簡單的切分處理，就可以自動形成規整的六面體網格，它比映射網格劃分方式具有更大的優勢和靈活性，一般情況下，要把復雜的幾何模型劃分成完全的六面體單元，通過幾何處理來分塊，再用掃略功能是最主要的劃分方法。

在ANSA下，情況也類似，ANSA是很具優勢的基于幾何的分網軟件，其建面功能十分強大，在沒有體這一概念的情況下，可以實現模型的分塊，操作簡單但效率很高，是未來分網軟件發展的大趨勢

混合網格劃分

混合網格劃分即在幾何模型上，根據各部位的特點，分別采用自由、映射、掃略等多種網格劃分方式，以形成綜合效果盡量好的有限元模型。混合網格劃分方式要在計算精度、計算時間、建模工作量等方面進行綜合考慮。

通常，為了提高計算精度和減少計算時間，應首先考慮對適合于掃略和映射網格劃分的區域先劃分六面體網格，應盡量通過切分等多種布爾運算手段來創建合適的區域（尤其是對所關心的區域或部位）；其次，對實在無法再切分而必須用四面體自由網格劃分的區域，采用帶中節點的六面體單元進行自由分網。

自由度耦合和約束方程

對于某些形式的復雜幾何模型，可以利用ANSYS的約束方程和自由度耦合功能（Abaqus中的tie功能）來促成劃分出優良的網格并降低計算規模。

比如，將相鄰的體在進行獨立的網格劃分（通常是采用映射或掃略方式）后再“粘結”起來，由于各個體之間在幾何上沒有聯系，因此不用費勁地考慮相互之間網格的影響，所以可以自由地采用多種手段劃分出良好的網格，而體之間的網格“粘結”是通過形函數差值來進行自由度耦合的，因此連接位置處的位移連續性可以得到絕對保證，如果非常關注連接處的應力，可以如下面所述再在該局部位置建立子區模型予以分析。

子模型等其它手段

子模型是一種先總體、后局部的分析技術（也稱為切割邊界條件方法），對于只關心局部區域準確結果的復雜幾何模型，可采用此手段，以盡量小的工作量來獲得想要的結果。

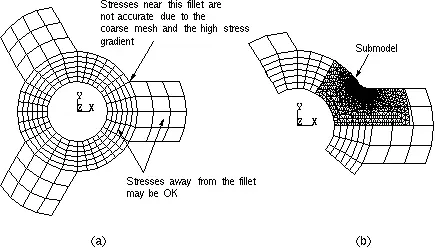
其過程是：先建立總體分析模型，并忽略模型中的一系列細小的特征，如導角、開孔、開槽等（因為根據圣維南原理，模型的局部細小改動并不特別影響模型總的分析結果），同時在該大模型上劃分較粗的網格（計算和建模的工作量都很小），施加載荷并完成分析。其次，（在與總體模型相同的坐標系下）建立局部模型，此時將前面忽略的細小特征加上，并劃分精細網格（模型的切割邊界應離關心的區域盡量遠），進行求解計算。

該方法的另外好處是：可以在小模型的基礎上優化（或任意改變）所關心的細小特征，如改變圓角半徑、縫的寬度等；總體模型和局部模型可以采用不同的單元類型，比如，總體模型采用板殼單元，局部模型采用實體單元等。

巧妙地利用結構的對稱性對實際工作大有好處，一是可以大大減少計算規模，二是可以便于施加準確的邊界條件，航空發動機渦輪盤的計算就是典型的例子。對于常規的結構和載荷都是軸對稱、循環對稱、平面對稱的問題，首先應利用其對稱性。

總之，對于復雜幾何模型，綜合運用多種手段建立起高質量、高計算效率的有限元模型就進行數值計算的最開始最關鍵的步驟，本文僅僅涉及到一些大的方向，實際問題涉及面廣，如網格過度與拓撲結構等相關處理都是網格劃分技術中經常遇到的問題，用戶只有在實際工作中不斷摸索、總結和驗證才能最終對復雜模型網格劃分計算掌握透徹，靈活運用。