引 言
在對本科生的教育過程中,有時會出現因學生成績過低、學分過少,而出現留級甚至延遲畢業的現象,這對學校和學生均造成了一定的負面影響。通過對學生成績數據的挖掘分析,可輔助教學管理,以便教師實施有效的教學活動,并刺激學生主動學習,幫助學生取得更好的成績。
文獻[1]利用數10種不同的神經網絡結構對學生成績進行預測。文獻[2]通過不同的分類模型,利用學生的校園卡數據和成績數據預測成績,其中多層分類器(MLPC)的效果最好。文獻[3]的研究中表明,傳統教師講授式課堂下學生的不及格率是學生主動學習的不及格率的1.5倍。因此,教師在教導學生相關的科目時,可以通過提供預測數據來及時警告,促進學生主動學習,從而降低不及格率。
文獻[4]使用神經網絡來預測學生的學習成績,結果顯示,用神經網絡算法比用線性回歸更準確。但在這項研究中,主要選擇了網上學習的成績來研究,沒有涉及線下面對面的教育方式。文獻[5]在分析中學生的成績時,利用人工神經網絡,從認知因素和心理因素兩個角度對學生的成績進行聚類。但心理因素的主觀性過強,容易影響結果的準確性。
神經網絡具有良好的學習性能,但也有較為明顯的缺點:收斂速度較慢、易陷入局部最小。用進化算法優化神經網絡可以在一定程度上解決此問題。其中,差分進化算法是一種高效的尋優算法,通過對個體差異的處理實現變異,適用于非連續不可微分或噪音較強的函數。文獻[6]證明了優化后的 DE?BPNN 模型預測效果要優于 GA ?BPNN、CS?BPNN 和 PSO ?BPNN 模型。利用差分進化優化神經網絡算法,也可以讓運算結果精度更高。
為了對大學生成績等級進行更精準的預測,本文提出一種自適應差分進化神經網絡模型,并對比了遺傳算法與差分進化算法的適應度曲線。結果表明,采用差分進化算法尋找最優權值閾值的效果較好。
1、自適應差分進化算法
自適應差分進化算法(Adaptive Differential EvolutionAlgorithm,ADE)是一種基于種群的全局搜索算法。常用的差分進化模式為 DE/rand/1/bin 和 DE/best/1/bin,第一種收斂速度慢于第二種,但第一種在種群的多樣性上較好,第二種易陷入局部最小值[8]。為了保持良好的多樣性,本文采用的模式為 DE/rand/1/bin,即隨機選擇當前種群的個體進行變異,差異向量個數為 1,且在交叉的模式中應用二項交叉。差分進化算法主要有以下幾個步驟:種群初始化、變異、交叉、選擇。本文引入自適應變異因子 F,其值隨迭代次數的增加而減小。
2、 ADE 優化 BP神經網絡算法
BP 神經網絡的特點為誤差反向傳播,具有較強的魯棒性和容錯性,但在運算中容易陷入局部最小,收斂速度較低[9]。神經網絡結構由輸入層、隱含層、輸出層三層組成。根據 Kolmogorov 定理[10]可知,隱含層層數為1 時,只要有足夠多的神經元節點數,就可以任意精度逼近任意非線性連續函數。當輸入層為 X1,X2,…,Xm,隱含層為 h1,h2,…,hn,輸出層為 Y 時,網絡拓撲結構如圖 1所示。
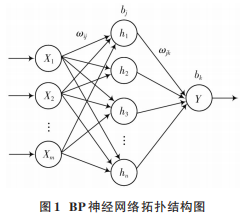
在該神經網絡中,從輸入層到隱含層的權值為ωij,閾值為bj,從隱含層到輸出層的權值為ωjk,閾值為bk。其中,i=1,2,…,m;j=1,2,…,n;k=1。逐層傳遞輸入信號后,在輸出層計算預測值與實際值的誤差。再根據所得誤差,結合學習率 η,返回修改并更新權值與閾值。若迭代尚未結束,則進行下一代計算。
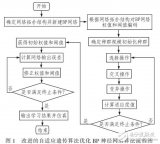
差分進化算法優化 BP 神經網絡的原理為:將神經網絡預測值與真實值的差值的均方誤差作為適應度函數,最終得到適應度值最小時的權值閾值,并作為新的神經網絡的權值閾值,最后進行求解。流程圖如圖 2所示。
3、 ADE?BP 神經網絡學生成績預測模型
3.1 數據預處理
為了便于后續數據的預測,并保證預測的準確性,首先要獲得正確且合適的數據,因此需要對數據進行預處理。從學校的服務器中調取出 2016 級的學生成績后,選擇某個學院的學生成績為本文的研究對象。提取出該學院所有學生從入學到大二下學期之間所有的課程成績,再選擇大三上學期的一門專業課成績作為被預測對象。由于在學生的所有成績中,“科目 h”這門課程的分數較低。為了凸顯本模型的預測效果,并預防教學事故,本文將“科目 h”的分數等級作為被預測數據。數據庫中的成績龐雜且部分數據不完整,因此接下來需要提高數據質量,對數據進行預處理:數據清洗、數據集成、數據轉換、數據歸約。
1)數據清洗:去除空白數據和異常數據。
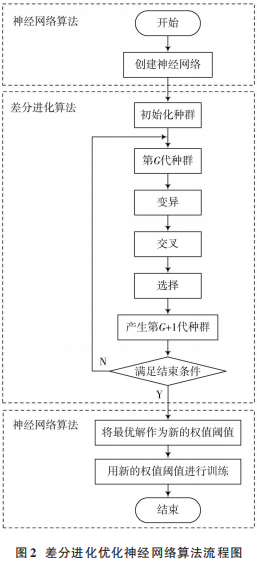
2)數據集成:將剩下的數據整理后,放在一個表格中,如表 1所示。
3)數據轉換:由于數據集維數較高,為了降低神經網絡的計算開銷,本文在得到學生各科分數后,將學生成績按照分數的不同層次劃分為5個等級:分數<60分,等級為 0;60≤分數<70,等級為 1;70≤分數<80,等級為2;80≤分數<90,等級為 3;90≤分數<100,等級為 4。等級越高,該門科目的成績越高,則該門科目的不及格率越低。
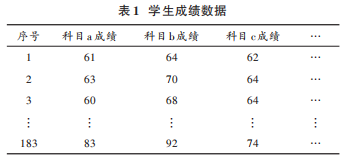
4)數據歸約:由于原始數據量過于龐大,僅留下和“科目 h”的課程屬性相同的科目,即均為“學科平臺課程”的 8門科目。
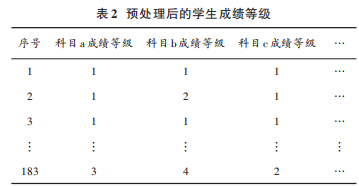
預處理后,得到 183條有效數據如表 2所示。
3.2 相關性分析
由于科目較多,為了簡化網絡結構,提高預測的效率,需要找出與被預測科目成績最相關的科目,作為神經網絡的輸入。因此,本文首先通過 SPSS 對所有科目的成績等級進行 Pearson 相關性分析。部分分析結果如表 3所示。
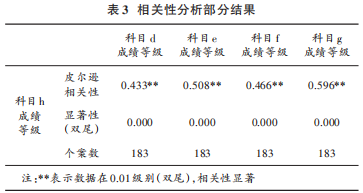
相關性分析的結果在 0.01級別顯著,則認為有 99%的把握認為相關系數顯著,該相關性分析結果具有統計學意義。由表 3 可知,本次相關性分析結果可以信任。本文選擇與“科目 h”這門課程相關性系數大于 0.45 的科目分數作為輸入數據,具體課程為:“科目 e”“科目 f”“科目 g”。
3.3 差分進化優化 BP神經網絡進行預測
3.3.1 輸入數據的歸一化
本模型利用 Matlab 實現神經網絡。首先將所有數據的順序打亂,并隨機選取 150 條作為訓練數據,33 條作為測試數據。為了提高模型準確度,再將所有數據行歸一化處理,使其值均在[-1,1]區間內。
3.3.2 輸入層、輸出層、隱含層節點數以及其他參數的選取
設置輸入層數據是與“科目 h”相關性系數大于等于 0.45 的三門課程的成績等級,輸入層神經元節點數為 3;隱含層神經元節點數的設定需要經過多次測試,最終發現節點數為 9 時正確率最高,因此隱含層神經元數設為9;輸出層為目標課程即“科目 h”的成績等級,其神經元節點數為1。本文神經網絡的隱含層節點轉移函數選擇 tansig 函數。輸出層節點轉移函數為 purelin函數。
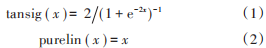
3.3.3 差分進化算法優化初始權值閾值
本模型中收斂誤差設置為 0.01。由于學習速率過小會導致速度降低,學習率過大會導致權值震蕩。結合經驗,將學習速率 η設為 0.05。
為了使權值可以具有較快的收斂速度,同時求解精度較高,設定種群規模 NP為 50,最大迭代次數 Gm為 30,縮放因子 F 隨迭代自適應變化,F 最小值為 0.2,最大值為 1.5,交叉因子 CR 為 0.9。所求問題的維數為:輸入層節點數×隱含層節點數+隱含層節點數×輸出層節點數+輸入層節點數+輸出層節點數。
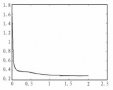
隨機產生初始種群后,進行變異與交叉操作。在交叉操作中,有指數交叉與二項交叉兩種方式。本文選用二項交叉。如果隨機數大于 CR,則被選入新個體。再以神經網絡訓練出的預測值與真實值做差,其均方誤差作為適應度函數。設置 GA?BP 的種群規模和最大迭代次數的值與 ADE?BP 的值一樣,交叉概率為 0.9,變異概率為 0.2。圖 3為差分進化優化 BP神經網絡的適應度變化曲線,圖 4 為遺傳算法優化神經網絡適應度變化的曲線。在達到最大迭代次數時,搜索出適應度值最小時的最優解。
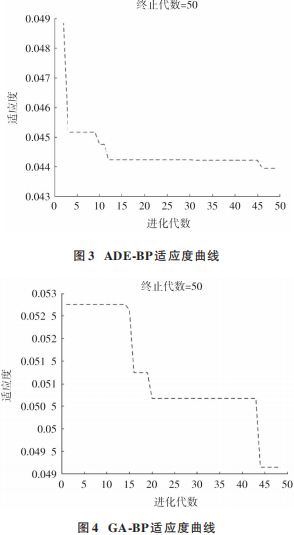
通過對比 ADE?BP 與 GA?BP 的適應度曲線,可以明顯看出,用自適應差分進化優化 BP 神經網絡的適應度下降更快,其誤差均方差的值約為 0.044。而遺傳算法優化神經網絡所得到的均方誤差值最終約為 0.049,可以看出,ADE?BP 的適應度更小,其均方差較小。因此可以得出,用自適應差分進化算法優化神經網絡能更快、更好地找到函數的最優值。
3.3.4 賦予神經網絡新的權值閾值并進行預測
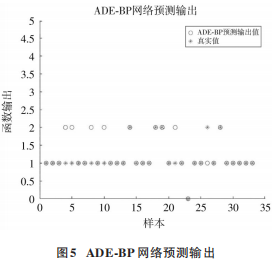
將搜索出的最優解轉換為神經網絡新的權值閾值,并對測試輸入數據進行預測。由于本文將分數數據轉換為 5 個等級,因此所有結果應為在區間[0,4]內的整數。因此對神經網絡的輸出值進行取整。設正確率為預測正確的數量與輸出數據的數量的比值。本模型得到 的 正 確 數 量 為 27,輸 出 數 據 總 共 33 個,正 確 率 為81.82%,MSE 為 0.181 8,并且誤差值均為1,可見誤差較小,認為預測效果較好。預測結果如圖 5所示。
4 、結 論
本文利用ADE算法和GA算法分別對神經網絡進行優化,可以看出,ADE 算法的收斂效果優于后者。利用學生的成績數據,結合 Matlab 實現了基于自適應差分進化的學生成績等級預測,并且該模型的預測效果較好。該模型在學生成績的預測中具有較強的實際意義,不僅可以讓學生進行有目的的主動學習、合理安排學習時間、提高科目的通過率,還能協助教師及時了解學生的學習情況,改善教學策略。在將來的研究中,可以進一步獲取學生多方面的信息,并進行量化,對大學生的期末成績進行深入研究。
審核編輯:郭婷
-
matlab
+關注
關注
185文章
2976瀏覽量
230484 -
神經網絡
+關注
關注
42文章
4771瀏覽量
100773
原文標題:論文速覽 | 基于自適應差分進化的學生成績等級預測神經網絡模型
文章出處:【微信號:現代電子技術,微信公眾號:現代電子技術】歡迎添加關注!文章轉載請注明出處。
發布評論請先 登錄
相關推薦
如何構建神經網絡?
卷積神經網絡模型發展及應用
自適應遺傳BP神經網絡模型在統計建模中的應用
加工過程的神經網絡模型參考自適應控制
一種改進的自適應遺傳算法優化BP神經網絡
基于反向學習的自適應差分進化算法
基于神經網絡模型參考自適應實現混合動力汽車電子差速控制系統的設計




 基于自適應差分進化的學生成績等級預測神經網絡模型
基于自適應差分進化的學生成績等級預測神經網絡模型










評論