生成模型希望可以生成符合真實分布(或給定數據集)的數據。我們常見的幾種生成模型有 GANs,Flow-based Models,VAEs,Energy-Based Models 以及我們今天希望討論的擴散模型 Diffusion Models。其中擴散模型和變分自編碼器 VAEs,和基于能量的模型 EBMs 有一些聯系和區別,筆者會在接下來的章節闡述。

▲ 常見的幾種生成模型
1、ELBO & VAE
在介紹擴散模型前,我們先來回顧一下變分自編碼器 VAE。我們知道 VAE 最大的特點是引入了一個潛在向量的分布來輔助建模真實的數據分布。
那么為什么我們要引入潛在向量?有兩個直觀的原因,一個是直接建模高維表征十分困難,常常需要引入很強的先驗假設并且有維度詛咒的問題存在。另外一個是直接學習低維的潛在向量,一方面起到了維度壓縮的作用,一方面也希望能夠在低維空間上探索具有語義化的結構信息(例如圖像領域里的 GAN 往往可以通過操控具體的某個維度影響輸出圖像的某個具體特征)。
引入了潛在向量后,我們可以將我們的目標分布的對數似然 logP(x),也稱為“證據evidence”寫成下列形式:

▲ ELBO的推理過程
其中,我們重點關注式 15。等式的左邊是生成模型想要接近的真實數據分布(evidence),等式右邊由兩項組成,其中第二項的 KL 散度因為恒大于零,所以不等式恒成立。如果在等式右邊減去該 KL 散度,則我們得到了真實數據分布的下界,即證據下界 ELBO。對 ELBO 進行進一步的展開,我們就可以得到 VAE 的優化目標。

▲ ELBO等式的展開
對該證據下界的變形的形式,我們可以直觀地這么理解:證據下界等價于這么一個過程,我們用編碼器將輸入 x 編碼為一個后驗的潛在向量分布 q(z|x)。我們希望這個向量分布盡可能地和真實的潛在向量分布 p(z) 相似,所以用 KL 散度約束,這也可以避免學習到的后驗分布 q(z|x) 坍塌成一個狄拉克 delta 函數(式 19 的右側)。而得到的潛在向量我們用一個解碼器重構出原數據,對應的是式 19 的左邊 P(x|z)。
VAE 為什么叫變分自編碼器。變分的部分來自于尋找最優的潛在向量分布 q(z|x) 的這個過程。自編碼器的部分是上面提到的對輸入數據的編碼,再解碼為原數據的行為。
那么提煉一下為什么 VAE 可以比較好地貼合原數據的分布?因為根據上述的公式推導我們發現:原數據分布的對數似然(稱為證據 evidence)可以寫成證據下界加上我們希望近似的后驗潛在向量分布和真實的潛在向量分布間的 KL 散度(即式 15)。如果把該式寫為 A=B+C 的形式。
因為 evidence(即 A)是個常數(與我們要學習的參數無關),所以最大化 B,也就是我們的證據下界,等價于最小化 C,也即是我們希望擬合的分布和真實分布間的差別。而因為證據下界,我們可以重新寫成式 19 那樣一個自編碼器的形式,我們也就得到了自編碼器的訓練目標。優化該目標,等價于近似真實數據分布,也等價于用變分手法來優化后驗潛在向量分布 q(z|x) 的過程。
但 VAE 自身依然有很多問題。一個最明顯的就是我們如何選定后驗分布 。絕大多數的 VAE 實現里,這個后驗分布被選定為了一個多維高斯分布。但這個選擇更多的是為了計算和優化的方便而選擇。這樣的簡單形式極大地限制了模型逼近真實后驗分布的能力。VAE 的原作者 kingma 曾經有篇非常經典的工作就是通過引入 normalization flow [1] 在改進后驗分布的表達能力。而擴散模型同樣可以看做是對后驗分布 的改進。
2、Hierarchical VAE
下圖展示了一個變分自編碼器里,潛在向量和輸入間的閉環關系。即從輸入中提取低維的潛在向量后,我們可以通過這個潛在向量重構出輸入。

▲ VAE里潛在向量與輸入的關系
很明顯,我們認為這個低維的潛在向量里一定是高效地編碼了原數據分布的一些重要特性,才使得我們的解碼器可以成功重構出原數據分布里的各式數據。那么如果我們遞歸式地對這個潛在向量再次計算“潛在向量的潛在向量”,我們就得到了一個多層的 HVAE,其中每一層的潛在向量條件于所有前序的潛在向量。
但是在這篇文章里,我們主要關注具有馬爾可夫性質的層級變分自編碼器 MHVAE,即每一層的潛在向量僅條件于前一層的潛在向量。

▲ MHVAE里的潛在向量只條件于上一層
對于該 MHVAE,我們可以通過馬爾可夫假設得到以下二式:

▲ 23和24式是用鏈式法則對依賴圖里的關系的拆解
對于該 MHVAE,我們可以用以下步驟推導其證據下界:

▲ MHVAE的變分下界推導
3、Variation Diffusion Model
我們之所以在談論擴散模型之前,要花如此大的篇幅介紹 VAE,并引出 MHVAE 的證據下界推導是因為我們可以非常自然地將擴散模型視為一種特殊的 MHVAE,該 MHVAE 滿足以下三點限制(注意以下三點限制也是整個擴散模型推斷的基礎):
潛在向量 Z 的維度和輸入 X 的維度保持一致。
每一個時間步的潛在向量都被編碼為一個僅依賴于上一個時間步的潛在向量的高斯分布。
每一個時間步的潛在向量的高斯分布的參數,隨時間步變化,且滿足最終時間步的高斯分布滿足標準高斯分布的限制。
因為第一點維度一致的原因,在不影響理解的基礎上,我們將 MHVAE 里的 Zt 表示為 Xt(其中 x0 為原始輸入),則我們可以將 MHVAE 的層級潛在向量依賴圖,重新畫為以下形式(即將擴散模型的中間擴散過程當做潛在向量的層級建模過程):

▲ 擴散過程的直觀解釋:在數據x0上不斷加高斯噪聲直至退化為純噪聲圖像Xt
直至這里,我們終于見到了我們熟悉的擴散模型的形式。
而在將上面的公式 25-28 里的 Zt 與 Xt 替換后,我們可以得到 VDM 里證據下界的推導公式里的前四行,即公式 34-37。并且在此基礎上,我們可以繼續往下推導。
37 至 38 行的變換是鏈式法則的等價替換(或上述公式 23 和 24 的變換),38 至 39 行是連乘過程的重組,39 至 40 行是對齊連乘符號的區間,40 至 41 行應用了 Log 乘法的性質,41 至 42繼續運用該性質進一步拆分,42 至 43 行是因為和的期望等于期望的和,43 至 44 是因為期望目標與部分時間步的概率無關可以直接省去,44 至 45 步是應用了KL 散度的定義進行了重組。

▲ VDM的證據下界推導
至此,我們又一次將原數據分布的對數似然,轉化為了證據下界(公式 37),并將其轉化為了幾項非常直觀的損失函數的加和形式(公式 45),他們分別為:
重構項,即從潛在向量 到原數據 的變化。在 VAE 里該重構項寫為 ,而在這里我們寫做 。
先驗匹配項。回憶我們上述提到的 MHVAE 里最終時間步的高斯分布應建立為標準高斯分布。
一致項。該項損失是為了使得前向加噪過程和后向去噪的過程中,Xt 的分布保持一致。直觀上講,對一個更混亂圖像的去噪應一致于對一個更清晰的圖像的加噪。而因為一致項的損失是定義于所有時間步上的,這也是三項損失里最耗時計算的一項。
雖然以上的公式推導給了我們一個非常直觀的證據下界,并且由于每一項都是以期望來計算,所以天然適用蒙特卡洛方法來近似,但如果優化該證據下界依然存在幾個問題:
我們的一致項損失是一項建立在兩個隨機變量 上的期望。他們的蒙特卡洛估計的方差大概率比建立在單個獨立變量上的蒙特卡洛估計的方差大。
我們的一致項是定義于所有時間步上的 KL 散度的期望和。對于 T 取值較高的情況(通常擴散模型 T 取 2000 左右),該期望的方差也會很大。
所以我們需要重新推導一個證據下界。而這個推導的關鍵將著眼于以下這個觀察:我們可以將擴散過程的正向加噪過程 重寫為 。之所以這樣重寫的原因是基于馬爾可夫假設,這兩個式子完全等價。于是對這個式子使用貝葉斯法則,我們可以得到式 46。

▲ 對前向加噪過程使用馬爾可夫假設和貝葉斯法則后的公式
基于公式 46,我們可以重寫上面的證據下界(式 37)為以下形式:其中式 47,48 和式 37,38 一致。式 49 開始,分母的連乘拆解由從 T 開始改為從 1 開始。式 50 基于上文提及的馬爾可夫假設對分母添加了 的依賴。式 51 用 log 的性質拆分了對數的目標。
式 52 代入了式 46 做了替換。式 53 將劃掉的分母部分連乘單獨提取出來后發現各項可約剩下式 54 部分的 。式 54 用 log 的性質消去了 得到了式 55。式 56 用 log 的性質拆分重組了公式,式 57 如同前述式 43-44 的變換,省去了無關的時間步。式 58 則用了 KL 散度的性質。

▲ 應用了馬爾可夫假設的擴散模型證據下界推導1

▲ 應用了馬爾可夫假設的擴散模型證據下界推導2
至此,我們應用了馬爾可夫假設得到了一個更優的證據下界推導。該證據下界同樣包含幾項直觀的損失函數:
重構項。該重構項與上面提及的重構項一致。
先驗匹配項。與上面提及的形式略有差別,但同樣是基于最終時間步應為標準高斯的先驗假設。
去噪匹配項。與上面提及的一致項的最大區別在于不再是對兩個隨機變量的期望。并且直觀上理解 代表的是后向的去噪過程,而 代表的是已知原始圖像和目標噪聲圖像的前向加噪過程。該加噪過程作為目標信號,來監督后向的去噪過程。該項解決了期望建立于兩個隨機變量上的問題。
注意,以上的推導完全基于馬爾可夫的性質所以適用于所有 MHVAE,所以當 T=1 的時候,以上的證據下界和 VAE 所推導出的證據下界完全一致!并且本文之所以稱為大一統視角,是因為對于該證據下界里的去噪匹配項,不同的論文有不同的優化方式。但歸根結底,他們的本質互相等價,且皆由該式展開推導得到。
下面我們會從擴散模型的角度做公式推導,來展開計算去噪匹配項。(注意第一版的推導里的一致項,也完全可以通過下一節的方式得到 q 和 p 的表達式,再通過 KL 來計算解析式)
4、Diffusion Model recap
在擴散模型里,有幾個重要的假設。其中一個就是每一步擴散過程的變換,都是對前一步結果的高斯變換(上一節 MHVAE 的限制條件 2):

▲ 與 MHVAE 不同,編碼器側的潛在向量分布并不經過學習得到,而是固定為線性高斯模型
這一點和 VAE 有很大不同。VAE 里編碼器側的潛在向量的分布是通過模型訓練得到的。而擴散模型里,前向加噪過程里的每一步都是基于上一步結果的高斯變換。其中 一般當作超參設置得到。這點對于我們計算擴散模型的證據下界有很大幫助。因為我們可以基于輸入 確切地知道前向過程里的某一步的具體狀態,從而監督我們的預測。
基于式 31,我們可以遞歸式地對 不斷加噪變換,得到最終 的表達式:

▲ 可以寫為關于 的一個高斯分布的采樣結果
所以對于式 58 里噪音匹配項里的監督信號,我們可以重寫成以下形式,其中根據式 70,我們可以得到 和 的表達式,而 因為是前向擴散過程,可以應用馬爾可夫性質看做 使用式 31 得到具體表達式。

▲ 式58里的監督信號可以通過 計算具體的值
代入每一項 q 所代表的高斯函數表達式后,我們最后可以得到一個新的高斯分布表達式,其中每一項都是具體可求的:

▲ 的解析形式
參考已經證明了前向加噪過程可以寫為一個高斯分布了。在擴散模型的初始論文 [2] 里提到,對于一個連續的高斯擴散過程,其逆過程與前向過程的方程形式(functional form)一致。所以我們將對去噪匹配項里的 也采用高斯分布的形式(更加具體的一些推導放在了末尾的補充里)。注意式 58 里,對兩個高斯分布求 KL 散度,其解析解的形式如下:

▲ 兩個高斯分布的KL散度解析解
我們現在已知其中一個高斯分布(左側)的參數,現在如果我們令右側的高斯分布和左側高斯分布的方差保持一致。那么優化該 KL 散度的解析式將簡化為以下形式:

▲ 式58的噪音匹配項簡化為最小化前后向均值的預測誤差
如此一來式 58 的噪音匹配項就被簡化為最小化前后向均值的預測誤差(式 92)。讀者請注意,以下的大一統的三個角度來看待 Diffusion model,實質上都是對式 92 里 的不同變形所推論出來的。其中 是關于 的函數,而 是關于 和t的函數。其中通過式 84,我們有 的準確計算結果,而因為 是關于 的函數。
我們可以將其寫為類似式 84 的形式(注意,有關為什么可以忽略方差并且讓均值選取這個形式放在了最末尾的補充討論里。但關于這個形式的選擇的深層原因實質上開辟了一個全新的領域來研究,并且關于該領域的研究直接導向了擴散模型之后的一系列加速采樣技術的出現)。

▲ 將后向預測的均值寫為類似前向加噪的形式
比較式 84 與 94 可知, 是我們通過噪音數據 來預測原始數據 的神經網絡。那么我們可以將式 58 里證據下界的噪音匹配項,最終寫為

▲ 噪聲匹配項的最終形式
那么,我們最后得到擴散模型的優化,最終表現為訓練一個神經網絡,以任意時間步的噪音圖像為輸入,來預測最初的原始圖像!此時優化目標轉化為了最小化預測誤差。同時式 58 上的對所有時間步的噪音匹配項求和的優化,可以近似為對每一時間步上的預測誤差的期望的最小值,而該優化目標可以通過隨機采樣近似:

▲ 該優化目標可以通過隨機采樣實現
5、Three Equivalent Perspective
為什么 Calvin Luo 的這篇論文叫做大一統視角來看待擴散模型?以上我們花了不菲的篇幅論證了擴散模型的優化目標可以最終轉化為訓練一個神經網絡在任意時間步從 預測原始輸入 。以下我們將論述如何通過對 不同的推導得到類似的角度看待擴散模型。
首先,我們已經知道給定每個時間步的噪聲系數 之后,我們可以由初始輸入 遞歸得到 。同理,給定 我們也可以求得 。那么對式 69 重置后,我們可以得到式 115。

▲ 將式69里的 和 關系重置后可得式115
重新將式 115 代入式 84 里,我們所得的關于時間步 t 的真實均值表達式 后,我們可以得到以下推導:

▲ 在推導真實均值時替換
注意在上一次推導的過程中, 里的 在計算 kl 散度的解析式時被抵消掉了,而 我們采取的是用神經網絡直接擬合的策略。而在這一次的推導過程中, 被替換成了關于 的表達式(關于 和 )后,我們可以得到 的新的表達式,依舊關于 ,只是不再與 相關,而是與 相關(式 124)。
其中,和式 94 一樣,我們忽略方差(將其設為與前向一致)并將希望擬合的 寫成與真實均值 一樣的形式,只是將 替換為神經網絡的擬合項后我們可以得到式 125。

▲ 與上次推導時替換 為神經網絡所擬合項一樣,這次換為擬合初始噪聲項
將我們新得到的兩個均值表達式重新代入 KL 散度的表達式里, 再次被抵消掉(因為 和 選取的形式一致)最終只剩下 和 的差值。注意式 130 和式 99 的相似性!

▲ 最終對證據下界里的去噪匹配項的優化可以寫成關于初始噪聲和其擬合項的差的最小化
至此,我們得到了對擴散模型的第二種直觀理解。對于一個變分擴散模型 VDM,我們優化該模型的證據下界既等價于優化其在所有時間步上對初始圖像的預測誤差的期望,也等價于優化在所有時間步上對噪聲的預測誤差的期望!事實上 DDPM 采取的做法就是式 130 的做法(注意 DDPM 里的表達式實際上用的是 ,關于這點在文末也會討論)。
下面筆者將概括第三種看待 VDM 的推導方式。這種方式主要來自于 SongYang 博士的系列論文,非常直觀。并且該系列論文將擴散模型這種離散的多步去噪過程統一成了一個連續的隨機微分方程(SDE)的特殊形式。SongYang 博士因此獲得了 ICLR 2021 的最佳論文獎!
后續來自清華大學的基于將該 SDE 轉化為常微分方程 ODE 后的采樣提速論文,也獲得了 ICLR 2022 的最佳論文獎!關于該論文的一些細節和直觀理解,Song Yang 博士在他自己的博客里給出了非常精彩和直觀的講解。有興趣的讀者可以點開本文初始的第二個鏈接查看。以下只對大一統視角下的第三種視角做簡短的概括。
第三種推導方式主要基于 Tweedie‘s formula。該公式主要闡述了對于一個指數家族的分布的真實均值,在給定了采樣樣本后,可以通過采樣樣本的最大似然概率(即經驗均值)加上一個關于分數(score)預估的校正項來預估。注意 score 在這里的定義是真實數據分布的對數似然關于輸入 的梯度。即

▲ score的定義
根據 Tweedie’s formula,對于一個高斯變量 z~N(mu_z, sigma_z) 來說,該高斯變量的真實均值的預估是:

▲ Tweedie’s formula對高斯變量的應用
我們知道在訓練時,模型的輸入 關于 的表達式如下

▲ 上文里的式70
我們也知道根據 Tweedie‘s formula 的高斯變量的真實均值預估我們可以得到下式

▲ 將式70的方差代入Tweedie’s formula
那么聯立兩式的關于均值的表達式后,我們可以得到 關于 score 的表達式 133

▲ 將 寫為關于score的表達式
如上一種推導方式所做的一樣,再一次重新將 的表達式代入式 84 對真實均值 的表達式里:(注意式 135 到 136 的變形主要在分子里最右邊的 到 ,約去了根號下 )

▲ 將 的關于score表達式代入式84
同樣,將 采取和 一樣的形式,并用神經網絡 來近似 score 后,我們得到了新的 的表達式 143。

▲ 關于score的 的表達式
再再再同樣,和上種推導里的做法一樣,我們再將新的 代入證據下界里 KL 散度的損失項我們可以得到一個最終的優化目標

▲ 將新的 的表達式代入證據下界的優化目標里
事實上,比較式 148 和式 130 的形式,可以說是非常的接近了。那么我們的 score function delta_p(xt) 和初始噪聲 是否有關聯呢?聯立關于 的兩個表達式 133 和 115 我們可以得到。

▲ score function和初始噪聲間的關系
讀者如果將式 151 代入 148 會發現和式 130 等價!直觀上來講,score function 描述的是如何在數據空間里最大化似然概率的更新向量。而又因為初始噪聲是在原輸入的基礎上加入的,那么往噪聲的反方向(也是最佳方向)更新實質上等價于去噪的過程。而數學上講,對 score function 的建模也等價于對初始噪聲乘上負系數的建模!
至此我們終于將擴散模型的三個形式的所有推導整理完畢!即對變分擴散模型 VDM 的訓練等價于訓練一個神經網絡來預測原輸入 ,也等價于預測噪聲 ,也等價于預測初始輸入在特定時間步的 score delta_logp(xt)。
讀到這里,相比讀者也已經發現,不同的推導所得出的不同結果,都來自于對證據下界里去噪匹配項的不同推導過程。而不同的變形,基本上都是利用了 MHVAE 里最開始提到的三點基本假設所得。
6、Drawbacks to Consider
盡管擴散模型在最近兩年成功出圈,引爆了業界,學術界甚至普通人對文本生成圖像的 AI 模型的關注,但擴散模型這個體系本身依舊存在著一些缺陷:
擴散模型本身盡管理論框架已經比較完善,公式推導也十分優美。但仍然非常不直觀。最起碼從一個完全噪聲的輸入不斷優化的這個過程和人類的思維過程相去甚遠。
擴散模型和 GAN 或者 VAE 相比,所學的潛在向量不具備任何語義和結構的可解釋性。上文提到了擴散模型可以看做是特殊的 MHVAE,但里面每一層的潛在向量間都是線性高斯的形式,變化有限。
而擴散模型的潛在向量要求維度與輸入一致這一點,則更加死地限制住了潛在向量的表征能力。
擴散模型的多步迭代導致了擴散模型的生成往往耗時良久。
不過學術界對以上的一些難題其實也提出了不少解決方案。比如擴散模型的可解釋性問題。筆者最近就發現了一些工作將 score-matching 直接應用在了普通 VAE 的潛在向量的采樣上。這是一個非常自然的創新點,就和數年前的 flow-based-vae 一樣。而耗時良久的問題,今年 ICLR 的最佳論文也將采樣這個問題加速和壓縮到了幾十步內就可以生成非常高質量的結果。
但是對于擴散模型在文本生成領域的應用最近似乎還不多,除了 prefix-tuning 的作者 xiang-lisa-li 的一篇論文 [3]
之外筆者暫未關注到任何工作。而具體來講,如果將擴散模型直接用在文本生成上,仍有諸多不便。比如輸入的尺寸在整個擴散過程必須保持一致就決定了使用者必須事先決定好想生成的文本的長度。而且做有引導的條件生成還好,要用擴散模型訓練出一個開放域的文本生成模型恐怕難度不低。
本篇筆記著重的是在探討大一統角度下的擴散模型推斷。但具體對 score matching 如何訓練,如何引導擴散模型生成我們想要的條件分布還沒有寫出來。筆者打算在下一篇探討最近一些將擴散模型應用在受控文本生成領域的方法調研里詳細記錄和比較一下
7、補充
關于為什么擴散核是高斯變換的擴散過程的逆過程也是高斯變換的問題,來自清華大神的一篇知乎回答里 [4] 給出了比較直觀的解釋。其中第二行是將 和 近似。第三行是對 使用一階泰勒展開消去了 。第四行是直接代入了 的表達式。于是我們得到了一個高斯分布的表達式。

▲ 擴散的逆過程也是高斯分布
在式 94 和式 125,我們都將對真實高斯分布 q 的均值 的近似 建模成了與我們所推導出的 一致的形式,并且將方差設置為了與 q 的方差一致的形式。
直觀上來講,這樣建模的好處很多,一方面是根據 KL 散度對兩個高斯分布的解析式來說,這樣我們可以約掉和抵消掉絕大部分的項,簡化了建模。另一方面真實分布和近似分布都依賴于 。在訓練時我們的輸入就是 xt,采取和真實分布形式一樣的表達式沒有泄漏任何信息。并且在工程上 DDPM 也驗證了類似的簡化是事實上可行的。但實際上可以這樣做的原因背后是從 2021 年以來的一系列論文里復雜的數理證明所在解釋的目標。同樣引用清華大佬 [4] 的回答:

▲ DDPM里簡化去噪的高斯分布的做法其實蘊含著深刻的道理
在 DDPM 里,其最終的優化目標是 而不是 。即預測的誤差到底是初始誤差還是某個時間步上的初始誤差。誰對誰錯?實際上這個誤解來源于我們對 關于 的表達式的求解中的誤解。
從式 63 開始的連續幾步推導,都應用到了一個高斯性質,即兩個獨立高斯分布的和的均值與方差等于原分布的均值和與方差和。而實質上我們在應用重參數化技巧求 的過程中,是遞歸式的不斷引入了新的 來替換遞歸中的 里的 。那么到最后,我們所得到的 無非是一個囊括了所有擴散過程中的 。這個噪聲即可以說是 t,也可以說是 0,甚至最準確來說應該不等于任何一個時間步,就叫做噪聲就好!

▲ DDPM的優化目標
關于對證據下界的不同簡化形式。其中我們提到第二種對噪聲的近似是 DDPM 所采用的建模方式。但是對初始輸入的近似其實也有論文采用。也就是上文提及的將擴散模型應用在可控文本生成的論文里 [3] 所采用的形式。該論文每輪直接預測初始 Word-embedding。而第三種 score-matching 的角度可以參照 SongYang 博士的系列論文 [5] 來看。里面的優化函數的形式用的是第三種。
審核編輯:郭婷
-
解碼器
+關注
關注
9文章
1144瀏覽量
40849 -
編碼器
+關注
關注
45文章
3659瀏覽量
134984
原文標題:從大一統視角理解擴散模型(Diffusion Models)
文章出處:【微信號:zenRRan,微信公眾號:深度學習自然語言處理】歡迎添加關注!文章轉載請注明出處。
發布評論請先 登錄
相關推薦
【推薦體驗】騰訊云自然語言處理
什么是自然語言處理?
自然語言處理怎么最快入門_自然語言處理知識了解
自然語言處理的優點有哪些_自然語言處理的5大優勢
基于深度學習的自然語言處理對抗樣本模型




 擴散模型應用在自然語言處理中的應用
擴散模型應用在自然語言處理中的應用
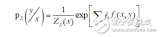










評論