平面度的測量及管控是我們產品最常見的一個規格，平常我們只是用設備測出產品平面度的數據，對其測試原理也是一知半解，當客戶對我們測試的數據產生質疑的時候，我們若不能合理解釋，則很難有效說服客戶；得不到客戶的信任，則我們的工作也很難進行下去。

平時，我們總簡單認為，平面度的測試就是用鏡頭到產品的最高點減去最低點即可，事實上，這樣的計算方法是錯誤的計算方法！平面度的本質是關心被測平面上各被測點之間的相互差異，并不關心各被測點和其他特征之間的差異。如果用高度差算，這個高度差會把上表面與下底面的平行誤差也引進來了，而這個平行誤差原本和上表面的平面度誤差無關。多余引入的平行誤差會使我們的數據大于產品的實際表現，及測出的結果偏高。

今天我們詳細介紹下3次元設備是如何利用點位去擬合基準平面從而得出產品的平面度數值的，其主要用到的數學原理就是最小二乘法，期間會有一些線性代數的矩陣加減乘除，矩陣的轉置等。不過我們可以直接用Excel表格來計算，將會簡單許多。

最小二乘法的擬合基準平面主要分為如下幾個步驟，我們將通過一個案例來逐步講解：

1. 擬合出最小二乘平面；

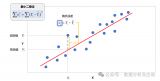
2. 找到最小二乘平面兩側的最遠采集點到該最小二乘平面的距離H1,H2（如下圖）；

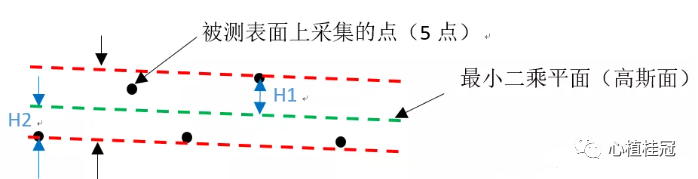
3. 通過計算出來的最遠點的距離H1和H2相加，即平面度的實測值；因為我們計算出的點到平面的距離有方向性，所以直接采用最大的距離減去最小的距離就是平面度的結果了。

01

擬合最小二乘平面

我們首先在產品下表面上采了9個點，點坐標如下圖：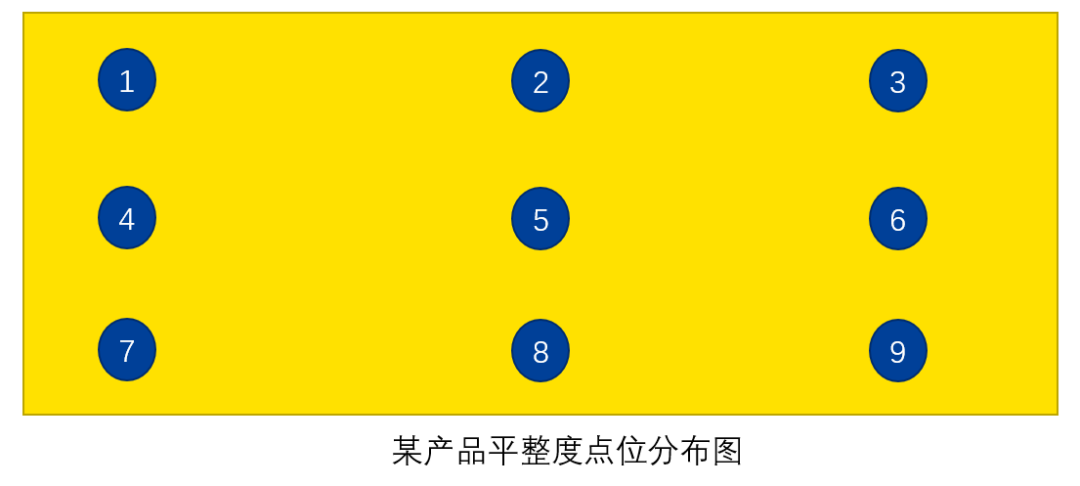

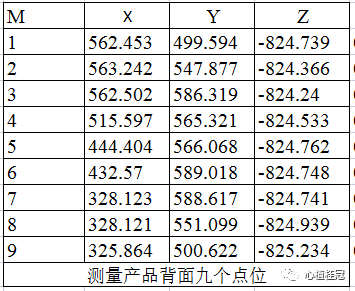
平面方程的公式為：z=ax+by+c 平面方中，a,b,c是平面方程的參數，只要知道a,b,c，我們就知道最小二乘法擬合出來的基準平面了。同樣的方法，把D1，D2...D9的x,y,z坐標值分別代入平面方程，可以得到下面的超定方程組:

接下來的思路是如何把它轉化成矩陣方程,如下：

則平面方程z=ax+by+c就可以寫成矩陣方程Ax=b 顯然A是已知的系數矩陣（代入坐標值就已知），x包含3個未知數a,b,c， b也是一個數據已知的矩陣（所有的已知z）。我們就可以套公式啦。

我們將原始的數據整理成A和b, 然后利用Excel的函數：

x=MMULT(MMULT(MINVERSE(MMULT(TRANSPOSE(A),A)),TRANSPOSE(A)),b)可以直接求出a,b,c。

Excel的具體數據如下：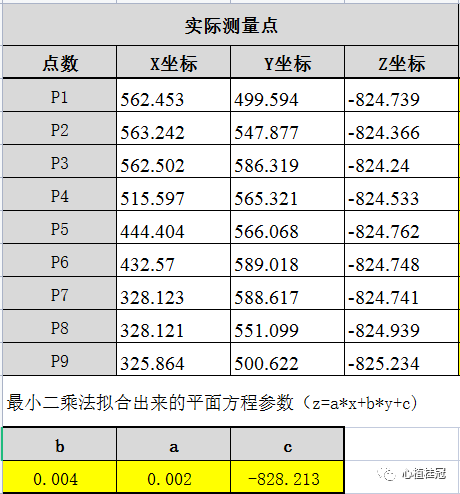



根據上表的計算，可以得到基準A的方程是：

z=0.02x+0.04y+(-828.213)

為了方便后邊直接套用公式，需要將上面這個基準平面的方程直接轉化標準平面方程：Ax+By+Cz+D=0, 轉化后為：

0.02x+0.04y+(-z)+(-828.213)=0

顯然，標準平面方程，我們可以得出: A=0.02, B=0.04,C=-1, D=-828.213, 這四個標準平面方程的參數在算距離的時候，馬上要用到的。

02

找到點到最小二乘平面的距離

然后再求被測要素上每一個點到該基準面的距離，就可以算出輪廓度。這里需要利用點到面的距離公式（A,B,C,D四個參數剛好可以在這里用上）：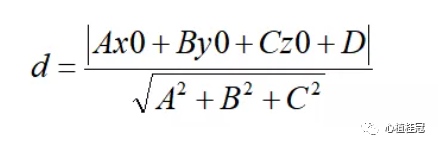



將被測要素每點的坐標代入上面點到面的公式，用點的實際坐標代該公式中的x0,y0,z0。計算出每點到基準面的距離，最后可以計算出輪廓度（按照ISO標準）。最后的計算結果參考下面的表格結果：

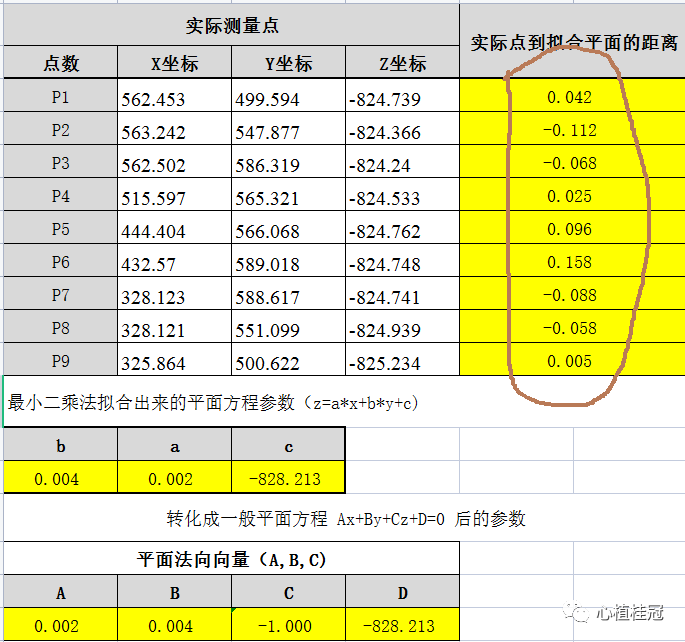
03

計算平面度

最后只要計算出被側面上每個點到基準面的距離，用最遠距離減去最近距離就是平行度了。結果如下圖：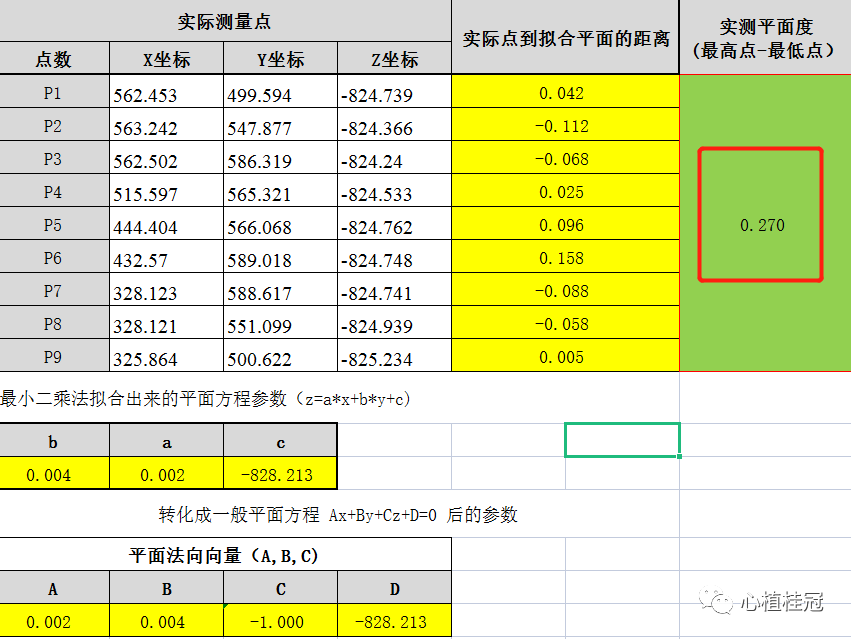

我們3次元實測結果如下圖：

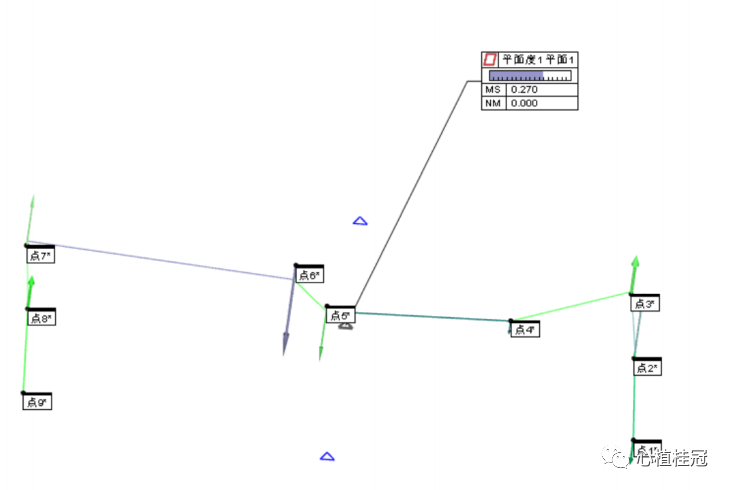
理論計算值與實測值結果一致，可見我們的理論計算是正確的。

04

結束語

本文主要講述了在已知被測平面上幾個點P的具體坐標的前提下，如何用Excel計算該面的平面度誤差的操作原理和方法。

本文分為三個部分進行講解，

1.計算平面度的基本原理，首先將已知點擬合成一個平面，再計算每個點到該平面的距離，距離的總寬度即表示平面度。

2.如何利用Excel的函數Linest()擬合出最小二乘平面以及具體的參數設置。

3.用Excel具體的計算過程和實現辦法。

審核編輯：劉清