統計力學和量子力學從歷史上看一直是互幫互助共同發展的. 當把統計力學的框架應用到由純粹的經典力學和經典電磁學描述的粒子系統時, 便會不可避免地產生佯謬以及與實驗對不攏的結果. 其中, 對比熱的研究可以說很大程度上暴露出經典力學的致命缺陷;對物質磁性的研究很大程度上暴露出經典電磁學的致命缺陷. 而這些致命缺陷的解決極大地推動了統計力學和量子力學的發展. 所以嚴格來看其實并沒有經典統計力學一說,所有被應用統計力學的系統必須完全基于純粹量子力學的描述. 本文將以理想單原子分子氣體, 理想雙原子分子氣體, 和理想非金屬固體為例, 應用統計力學的框架探討在經典力學描述和量子力學描述下這三種系統的比熱, 并由此展示量子力學是如何克服經典力學對比熱估計的缺陷的. 由于篇幅所限, 本文不可能從零開始講起. 故假定讀者已對熱力學第0, 1, 2, 3定律, 能均分定理(注意它只是個經典定理), 正則系綜框架下計算各種熱力學量的基本流程(核心是計算配分函數)和量子力學的三個玩具模型(無限深勢阱, 氫原子, 和諧振子)有初步的理解.
1理想單原子分子氣體的比熱問題
假定一個由 個完全相同的無相互作用的粒子構成的氣體體系. 整個體系被關在一個體積是 的盒子里. 每個粒子只由一個原子組成(比如一些稀有氣體). 由于粒子間沒有相互作用勢能, 故體系總能量就是每個粒子的平動動能之和. 考慮到每個粒子有 , , 三個自由度, 所以體系哈密頓量可以寫成:
當我們考慮經典力學的表述時, 上式的 是連續變化的, 與之對應的廣義坐標 也是連續變化的. 所以體系的正則配分函數是:
注意上式的 和 分別是量子全同性原理(全同粒子不可區分)和量子不確定性原理在經典配分函數中的體現(等效為這兩個保留下來的因子). 但由于我們這果要計算的是內能 (然后由此得出比熱), 即配分函數的對數對逆溫 的偏導數, 而 因子中并不包含 , 所以對于本計算而言該因子只是個并不重要的常數. 將 的表達式代入配分函數然后化簡得到:
所以體系的內能是:
很容易發現這個內能的結果和經典的能均分定理給出的結論是完全一致的. 在此基礎上, 我們可以進一步求出比熱:
所以在經典情形下算出的比熱是一個與溫度 無關的常數. 這個結果在高溫下沒問題, 但在低溫下( 接近絕對零度時) 直接與熱力學第三定律矛盾! 熱力學第三定律要求熵和墑的一階變化率(比熱)在 趨向 K時必須為 0 ! 而上面這個比熱的結果在趨向于 K時仍為 而不是0. 要解決這個問題就必須借助量子力學!
在上面的計算中, 我們采用的是經典力學對粒子的描述, 即 是連續變化的. 但如果采用的是量子力學的描述, 因為此時粒子被束俌在一個體積是 的點子里(也就是一個三維無限深勢阱里), 那么根據量子力學里關于無限深勢阱束縛態的結論, 就必然不是連續變化的, 而是只能取一系列分立的值:
其中 取正整數. 所以體系的哈密頓量可以寫成:
由于此時狀態是分立的, 所以體系的正則配分函數是:
代入 的表達式得到:
其中 . 在高溫下, 很小, 所以上面的求和可以近似成積分:
因此可以看出高溫下量子配分函數退化到經典情形的配分函數. 所以根據之前的計算結果, 高溫下比熱是 . 然而當溫度 趨于0 K, 也就是 趨向 時, 前面說的求和近似成積分的技巧并不適用. 所以我們只能老老實實地回到量子配分函數的原始級數表示.
值得注意的是:括號內的級數并不是簡單的等比級數, 所以我們并不能把它直接求出來. 但是注意到這個級數的每一項都比前一項小得多(因為此時 很大). 所以我們可以只取這個級數的前兩項作為這個級數的近似, 以便于后面比熱的計算. 所以在低溫下量子配分函數可以近似成:
所以體系的內能是:
進一步求出低溫下比熱是:
可以發現當溫度 趨于 0 K時,
所以在對粒子采用量子力學的描述以后, 低溫下比熱的行為恰好滿足熱力學第三定律!
2理想雙原子分子氣體的比熱問題
考慮和情形(1)幾乎完全相同的理想氣體體系, 除了把里面的單原子分子都換成雙原子分子 (比如氧氣, 氫氣,一氧化碳). 在使用質心坐標和相對坐標后,一個雙原子分子的總自由度可以等效成 3 個質心平動自由度(這塊和單原子分子沒區別), 再加上比單原子分子多出來的內稟自由度, 即兩個轉動自由度 , , 和一個軸向的振動自由度(注意一個軸向的振動自由度其實對應到哈密頓量里兩個獨立的平方項, 即一個平動動能項和一個彈性勢能項). 在經典力學的描述下, 根據能均分定理, 哈密頓量里每個獨立的平方項都對應到 的平均能量. 一個雙原子分子根據上述分析共有 7 個獨立的平方項, 所以貢獻 的平均能量. 所以 個雙原子分子頁獻 的平均能量(也就是內能 . 所以比熱 constant. 也就是比熱是一個與溫度 無關的常數. 而實驗的觀測結果發現比熱隨溫度 的依賴關系是一個類似階梯型的函數:在極高溫下, , 隨著溫度降低, , 溫度再降低, , 然后溫度再降低到接近0 K, . 要解決這個問題同樣也必須借助量子力學!
在量子力學的描述下, 一個雙原子分子的平動自由度可以看成是三維無限深勢阱模型, 轉動自由度可以看成是氫原子模型, 振動自由度可以看成是一維諧振子模型. 所以根據量子力學中這三個玩具模型的結論, 我們可以寫出 個雙原子分子總的哈宓頓量:
所以體系的正則配分函數是:
所以體系的內能是:
其中
在情形(1)中已經處理過 . 所以我們現在著重看 和 . 當高溫 很大也就是很小時, 可以被近似成如下的積分形式:
所以高溫下轉動能級部分給出的比熱是:
此結果與經典的能均分定理給出的結論一致.
當溫度 很低也就是 很大時, 完全仿照(1)中的邏輯, 因為原始的無窮級數難以計算, 所以我們只取該級數的前兩項作為近似,
所以低溫下轉動能級部分給出的比熱是:
可以發現當溫度 趨于0 K時,
所以零溫下比熱是 0 , 滿足熱力學第三定律!
現在來看 . 容易發現 表達式里的無窮級數剛妤是個簡單的等比級數, 所以:
在高溫 下, 很小, 所以
所以高溫下振動能級部分給出的比熱是:
此結果與經典的能均分定理給出的結論一致.
當溫度 很低也就是 很大時,
這個結果剛好對應零溫時 個諧振子的總的基態零點能. 所以零溫下振動能級給出的比熱是:
滿足熱力學第三定律! 平動, 轉動和振動能級都被凍結, 所以對比熱的貢獻是 0. 當溫度從0 K逐漸升高, 最先被激發的是質心的平動自由度, 使得比熱從 0 逐漸增加到 的平臺. 繼續往上升高溫度, 內部的轉動自由度也被激發出來, 使得比熱從 的平臺逐漸增加到 的平臺 (室溫就在比熱差不多是 的區間里, 此時只有平動和轉動自由度被激發). 再往上提升溫度到極高溫, 內部的振動自由度也最終被激發出來, 從而使得比熱最終飽和至 的平臺.
3理想非金屬固體的比熱問題(晶體比熱問題)
考慮一個由 個原子構成的三維理想固體. 這 個原子在空間周期性排列組成晶格. 每個原子都在自己的平衡位置附近做簡諧振動. 在簡正坐標下, 這個系統可以被看成是 個獨立的一維諧振子的聯合. 在諧振子的經典力學描述下, 根據能均分定理, 每個一維諧振子哈密頓量里包含兩個獨立的平方項(一個平動動能項和一個彈性勢能項), 所以貢獻 的內能, 也就是貢獻 的比熱. 故 個諧振子的聯合總共貢獻 的比熱. 這個 的比熱是個與溫度無關的常數. 所以很明顯在低溫下這個結果不趨于0, 所以與熱力學第三定律矛盾! 然而, 如果使用諧振子的量子力學描述, 問題可以被順利地解決! 在量子力學的描述下, 簡正坐標表象下的哈密頓量可以被對角化成:
所以體系的正則配分函數是:
考慮最簡單的情形:所有振子都是相同的頻率 , 也就是諧振子的狀態密度相對于頻率(能量)的分布取成狄拉克delta函數的形式. (注:這種過于簡化的態密度的取法被叫做 “愛因斯坦模型”, 更加合理的態密度取法是將其取成關于頻率的二次式, 即所謂的“德拜模型”. 我們這里為了簡化起見只考慮“愛因斯坦模型”). 此時體系的正則配分函數可以簡化成:
所以體系內能是:
在高溫 下也就是 很小時,
所以高溫下的晶體比熱是:
此結果與經典的能均分定理給出的結論一致.
在低溫 下(趨于絕對零度) 也就是 很大時,
所以零溫下的晶體比熱是 0, 滿足熱力學第三定律!
圖 1 和圖 2 分別直觀地給出了經典描述和量子描述下內能和比熱與溫度 的函數關系曲線:
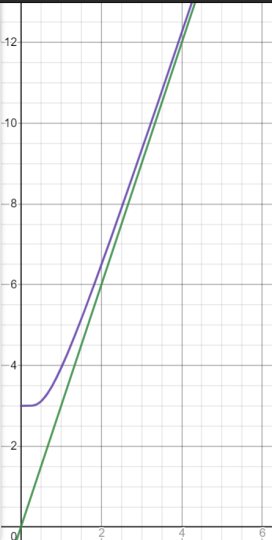 圖1 - 綠線是經典描述下的內能-溫度關系, 紫線是量子描述下的內能-溫度關系. 可以看出低溫下由于量子效應顯著導致紫線偏離綠線很大, 但隨著溫度升高, 量子效應越來越不明顯, 導致綠線和紫線逐漸靠近直至基本重合.
圖1 - 綠線是經典描述下的內能-溫度關系, 紫線是量子描述下的內能-溫度關系. 可以看出低溫下由于量子效應顯著導致紫線偏離綠線很大, 但隨著溫度升高, 量子效應越來越不明顯, 導致綠線和紫線逐漸靠近直至基本重合. 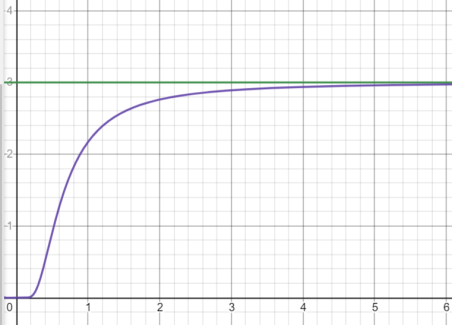 圖2 - 綠線是經典描述下的比熱-溫度關系, 紫線是量子描述下的比熱-溫度關系. 可以看出低溫下兩者有巨大的差別. 經典的能均分定理給出了非零的常數比熱. 而使用了諧振子的量子描述以后, 綠線被修正成了紫線. 此時低溫下滿足熱力學第三定律同時高溫下退化成經典的綠線!
圖2 - 綠線是經典描述下的比熱-溫度關系, 紫線是量子描述下的比熱-溫度關系. 可以看出低溫下兩者有巨大的差別. 經典的能均分定理給出了非零的常數比熱. 而使用了諧振子的量子描述以后, 綠線被修正成了紫線. 此時低溫下滿足熱力學第三定律同時高溫下退化成經典的綠線!
-
計算
+關注
關注
2文章
450瀏覽量
38833 -
函數
+關注
關注
3文章
4333瀏覽量
62723 -
熱力學
+關注
關注
0文章
43瀏覽量
9314
原文標題:統計力學 – 比熱問題
文章出處:【微信號:bdtdsj,微信公眾號:中科院半導體所】歡迎添加關注!文章轉載請注明出處。
發布評論請先 登錄
相關推薦
量子力學原理下載
關于二極管的半導體物理學
軟體機器人學習問題探討
前沿量子力學理論與實踐探討續(一)
對電力系統計算機應用存在問題及解決方法進行了探討
電池使用情況統計信息
基于云計算的監控與統計
熱力學統計物理第四版的課后答案合集免費下載

關于量子力學基本原理的幾個題目




 應用統計力學的框架探討
應用統計力學的框架探討











評論