對(duì)抗訓(xùn)練本質(zhì)是為了提高模型的魯棒性,一般情況下在傳統(tǒng)訓(xùn)練的基礎(chǔ)上,添加了對(duì)抗訓(xùn)練是可以進(jìn)一步提升效果的,在比賽打榜、調(diào)參時(shí)是非常重要的一個(gè)trick。對(duì)抗訓(xùn)練在CV領(lǐng)域內(nèi)非常常用,那么在NLP領(lǐng)域如何使用呢?本文簡(jiǎn)單總結(jié)幾種常用的對(duì)抗訓(xùn)練方法。
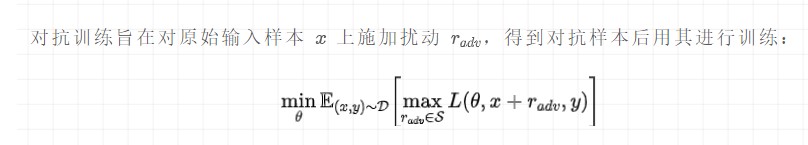
公式理解:
最大化擾動(dòng):挑選一個(gè)能使得模型產(chǎn)生更大損失(梯度較大)的擾動(dòng)量,作為攻擊;
最小化損失:根據(jù)最大的擾動(dòng)量,添加到輸入樣本后,朝著最小化含有擾動(dòng)的損失(梯度下降)方向更新參數(shù);
這個(gè)被構(gòu)造出來的“對(duì)抗樣本”并不能具體對(duì)應(yīng)到某個(gè)單詞,因此,反過來在推理階段是沒有辦法通過修改原始輸入得到這樣的對(duì)抗樣本。
對(duì)抗訓(xùn)練有兩個(gè)作用,一是 提高模型對(duì)惡意攻擊的魯棒性 ,二是 提高模型的泛化能力 。
在CV任務(wù),根據(jù)經(jīng)驗(yàn)性的結(jié)論,對(duì)抗訓(xùn)練往往會(huì)使得模型在非對(duì)抗樣本上的表現(xiàn)變差,然而神奇的是,在NLP任務(wù)中,模型的泛化能力反而變強(qiáng)了。
常用的幾種對(duì)抗訓(xùn)練方法有FGSM、FGM、PGD、FreeAT、YOPO、FreeLB、SMART。本文暫時(shí)只介紹博主常用的3個(gè)方法,分別是 FGM 、 PGD 和 FreeLB 。
具體實(shí)現(xiàn)時(shí),不同的對(duì)抗方法會(huì)有差異,但是 從訓(xùn)練速度和代碼編輯難易程度的角度考慮,推薦使用FGM和迭代次數(shù)較少的PGD 。
一、FGM算法

FGM的代碼量很少,只需要自行實(shí)現(xiàn)簡(jiǎn)單的類即可:
importtorch classFGM(): def__init__(self,model): self.model=model self.backup={}#用于保存模型擾動(dòng)前的參數(shù) defattack( self, epsilon=1., emb_name='word_embeddings'#emb_name表示模型中embedding的參數(shù)名 ): ''' 生成擾動(dòng)和對(duì)抗樣本 ''' forname,paraminself.model.named_parameters():#遍歷模型的所有參數(shù) ifparam.requires_gradandemb_nameinname:#只取wordembedding層的參數(shù) self.backup[name]=param.data.clone()#保存參數(shù)值 norm=torch.norm(param.grad)#對(duì)參數(shù)梯度進(jìn)行二范式歸一化 ifnorm!=0andnottorch.isnan(norm):#計(jì)算擾動(dòng),并在輸入?yún)?shù)值上添加擾動(dòng) r_at=epsilon*param.grad/norm param.data.add_(r_at) defrestore( self, emb_name='word_embeddings'#emb_name表示模型中embedding的參數(shù)名 ): ''' 恢復(fù)添加擾動(dòng)的參數(shù) ''' forname,paraminself.model.named_parameters():#遍歷模型的所有參數(shù) ifparam.requires_gradandemb_nameinname:#只取wordembedding層的參數(shù) assertnameinself.backup param.data=self.backup[name]#重新加載保存的參數(shù)值 self.backup={}
在訓(xùn)練時(shí),只需要額外添加5行代碼:
fgm=FGM(model)#(#1)初始化 forbatch_input,batch_labelindata: loss=model(batch_input,batch_label)#正常訓(xùn)練 loss.backward()#反向傳播,得到正常的grad #對(duì)抗訓(xùn)練 fgm.attack()#(#2)在embedding上添加對(duì)抗擾動(dòng) loss_adv=model(batch_input,batch_label)#(#3)計(jì)算含有擾動(dòng)的對(duì)抗樣本的loss loss_adv.backward()#(#4)反向傳播,并在正常的grad基礎(chǔ)上,累加對(duì)抗訓(xùn)練的梯度 fgm.restore()#(#5)恢復(fù)embedding參數(shù) #梯度下降,更新參數(shù) optimizer.step() model.zero_grad()
二、PGD算法
Project Gradient Descent(PGD)是一種迭代攻擊算法,相比于普通的FGM 僅做一次迭代,PGD是做多次迭代,每次走一小步,每次迭代都會(huì)將擾動(dòng)投射到規(guī)定范圍內(nèi)。形式化描述為:

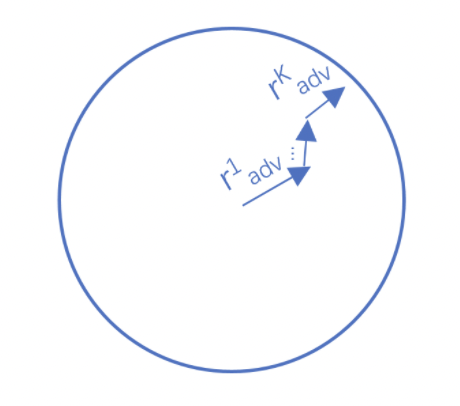
代碼實(shí)現(xiàn)如下所示:
importtorch classPGD(): def__init__(self,model): self.model=model self.emb_backup={} self.grad_backup={} defattack(self,epsilon=1.,alpha=0.3,emb_name='word_embeddings',is_first_attack=False): forname,paraminself.model.named_parameters(): ifparam.requires_gradandemb_nameinname: ifis_first_attack: self.emb_backup[name]=param.data.clone() norm=torch.norm(param.grad) ifnorm!=0andnottorch.isnan(norm): r_at=alpha*param.grad/norm param.data.add_(r_at) param.data=self.project(name,param.data,epsilon) defrestore(self,emb_name='word_embeddings'): forname,paraminself.model.named_parameters(): ifparam.requires_gradandemb_nameinname: assertnameinself.emb_backup param.data=self.emb_backup[name] self.emb_backup={} defproject(self,param_name,param_data,epsilon): r=param_data-self.emb_backup[param_name] iftorch.norm(r)>epsilon: r=epsilon*r/torch.norm(r) returnself.emb_backup[param_name]+r defbackup_grad(self): forname,paraminself.model.named_parameters(): ifparam.requires_grad: self.grad_backup[name]=param.grad.clone() defrestore_grad(self): forname,paraminself.model.named_parameters(): ifparam.requires_grad: param.grad=self.grad_backup[name]
pgd=PGD(model) K=3 forbatch_input,batch_labelindata: #正常訓(xùn)練 loss=model(batch_input,batch_label) loss.backward()#反向傳播,得到正常的grad pgd.backup_grad() #累積多次對(duì)抗訓(xùn)練——每次生成對(duì)抗樣本后,進(jìn)行一次對(duì)抗訓(xùn)練,并不斷累積梯度 fortinrange(K): pgd.attack(is_first_attack=(t==0))#在embedding上添加對(duì)抗擾動(dòng),firstattack時(shí)備份param.data ift!=K-1: model.zero_grad() else: pgd.restore_grad() loss_adv=model(batch_input,batch_label) loss_adv.backward()#反向傳播,并在正常的grad基礎(chǔ)上,累加對(duì)抗訓(xùn)練的梯度 pgd.restore()#恢復(fù)embedding參數(shù) #梯度下降,更新參數(shù) optimizer.step() model.zero_grad()
三、FreeLB算法


很明顯找到FreeLB與PGD的區(qū)別在于累積的方式:
FreeLB:通過對(duì) K K K 次梯度的平均累積作為擾動(dòng)更新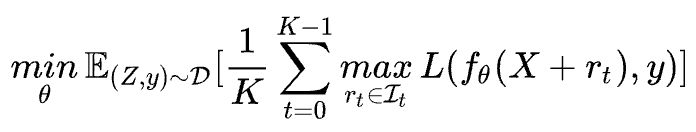
PGD:只取最后一次的梯度進(jìn)行更新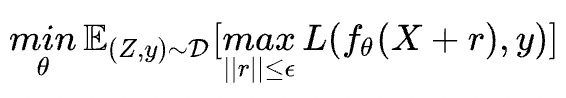
實(shí)現(xiàn)流程如下圖所示: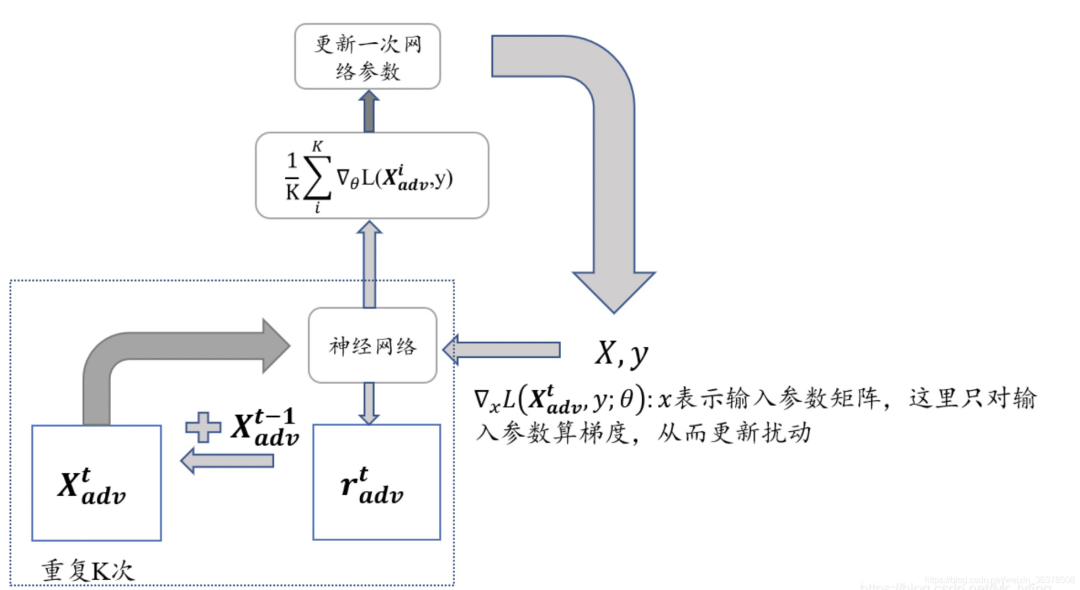
審核編輯:劉清
-
算法
+關(guān)注
關(guān)注
23文章
4615瀏覽量
93025 -
nlp
+關(guān)注
關(guān)注
1文章
489瀏覽量
22052
原文標(biāo)題:煉丹之道 | NLP中的對(duì)抗訓(xùn)練
文章出處:【微信號(hào):zenRRan,微信公眾號(hào):深度學(xué)習(xí)自然語言處理】歡迎添加關(guān)注!文章轉(zhuǎn)載請(qǐng)注明出處。
發(fā)布評(píng)論請(qǐng)先 登錄
相關(guān)推薦
簡(jiǎn)述電子對(duì)抗綜合模擬訓(xùn)練平臺(tái)
優(yōu)化神經(jīng)網(wǎng)絡(luò)訓(xùn)練方法有哪些?
微軟在ICML 2019上提出了一個(gè)全新的通用預(yù)訓(xùn)練方法MASS

新的預(yù)訓(xùn)練方法——MASS!MASS預(yù)訓(xùn)練幾大優(yōu)勢(shì)!

關(guān)于語言模型和對(duì)抗訓(xùn)練的工作

NLP中的對(duì)抗訓(xùn)練到底是什么
現(xiàn)代交互技術(shù)下的兒童語言表達(dá)訓(xùn)練方法
總結(jié)幾種常用的單片機(jī)加密方法

時(shí)識(shí)科技提出新脈沖神經(jīng)網(wǎng)絡(luò)訓(xùn)練方法 助推類腦智能產(chǎn)業(yè)落地
幾種常用的NLP數(shù)據(jù)增強(qiáng)方法
傳感器使用中幾種常用的簡(jiǎn)單處理方法
淺談傳感器幾種常用的簡(jiǎn)單處理方法
混合專家模型 (MoE)核心組件和訓(xùn)練方法介紹




 簡(jiǎn)單總結(jié)幾種NLP常用的對(duì)抗訓(xùn)練方法
簡(jiǎn)單總結(jié)幾種NLP常用的對(duì)抗訓(xùn)練方法










評(píng)論