一、背景
極光藍包裝盒成潮流標識,得物App成年輕潮人精神歸屬,特殊的包裝材料已經在消費者之間形成了強大的心智,極光藍等于得物。
但是由于早期箱型尺寸數據由人工經驗設計,出現包裝箱尺寸和商品尺寸匹配度不高的問題,一般會造成以下影響:
不合理的紙箱尺寸導致部分商品使用了較大的紙箱,造成了紙箱采購成本的浪費。
較大紙箱會造成運輸成本的增加。
商品和紙箱之間的空隙過大,可能在運輸過程中造成商品的損壞。
二、確定方案
考慮到紙箱招標節奏以及還需要留給倉內打樣試裝,試發貨的時間,所以需要用比較快的速度完成建模和計算。
在這件事上,業務方也無法給出一些特別明確的準則,例如具體要算的綜合目標中是包含運輸成本的,這之中包含承運商的分配算法規則和他們的運費模板,將這些因素直接納入到箱型建模之中基本是不可能的,再如箱子的數量是影響采購招標談判的成本以及倉內的人效的,這里很難量化,也無法直接定義箱型數量值的評判標準。因此首先要和業務方產品分析現狀定義目標,將問題全部量化,同時去簡化問題。
2.1 問題分析
sku數據:過去一年的發貨sku主數據及其對應的銷量,再排除規則之外(只考慮用紙箱包裝發貨的商品、排除異性箱包裝商品)和異常值(如sku尺寸異常)。
紙箱尺寸參數約束:考慮面單尺寸(紙箱尺寸下限定義)和便于倉內人員打包等合理性(紙箱尺寸上限定義),我們確定了紙箱上下限,形成數百萬組合的空間。
箱型數約束:排除異型箱,需綜合考慮裝箱率、采購成本和倉內效率,一般來說單倉的箱型數量不宜超過15個。
覆蓋率約束:在已經篩選出紙盒外包裝打包的sku的前提下,接受部分異形、大件物品不可被箱型組覆蓋,要求覆蓋發貨訂單率>=99%。
基于以上對問題的分析可以看出,如果有了一組解K個箱型,去計算裝箱率,這個問題的復雜度還好。但是如果正面去計算,則需對符合條件的sku去遍歷箱型組合,這個基本上是無法在有效時間內算出結果的。
2.2 問題簡化
2.2.1 箱型數約束
排除異型箱,基于得物當前的倉內實際情況,本次預計新設計的箱子數在8~15個,需綜合考慮裝箱率、采購成本和倉內效率,當箱型數量增加時,裝箱率會提高,采購成本也會提高,倉內效率會降低。
由于這里并不能量化它,例如給出具體綜合指數,因此此處決定給出多個版本,供業務方抉擇,而不作為建模的約束或目標,這里相當于直接簡化為把M組箱型的M * 固定一種箱型的復雜度,在實際中開發中,只需要用M個容器同時執行一次計算即可。
2.2.2 覆蓋率約束
覆蓋率約束是個不等式約束,且當前問題,不可覆蓋的sku部分的分布是非常顯而易見的,集中在長寬高中一個或多個值超過倉內操控方便程度上限值,因此,這里將箱型上限值和接受不覆蓋的部分,再建模之前先確定下來。
2.2.3 目標函數定義
對于采購成本來說,這不必說,一定和紙箱的用紙情況有關,紙箱用紙越小(紙箱展開面積越小)則成本越低;
對于運輸成本來說,基本上3pl都是用MAX(拋重,實重)的方法來計算,那么這和紙箱展開面積的優化方向也是正的;
如果把各3pl運費模板加入到建模中,同時也需要考慮承運商分配的算法設計,那么問題會過于復雜,計算量也是很大。現在很顯然,我們只要優化單均用紙面積,如果某單優化后的紙箱包裝未觸及運費模板的變動范圍,則運費不變,若觸及則運費成本必然會降低。
綜上,最終考慮用裝箱率這個間接指標作為目標,裝箱率指的是測試的(數據集sku總體積 / 數據集發貨箱子總體積),這個也是產品和業務方很熟悉且一直在關注的指標。
2.2.4 問題建模
經過上述簡化,這里將目標函數定義成了裝箱率,并且發貨訂單覆蓋率、箱型數約束值放在了建模問題之外。
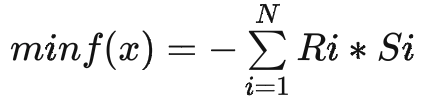
其中,S_i表示Sku_i的銷量,R_i表示Sku_i的推薦箱型結果裝箱率 推薦箱型應滿足內部間隙大于最低要求,在箱型組中選擇最小箱型,即
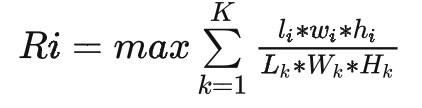
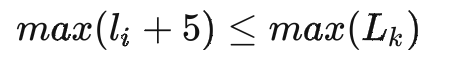
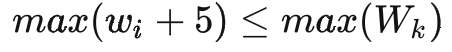
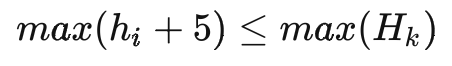
箱子的大小,應滿足至少可以貼運單,也不能過大影響倉內人員打包效率
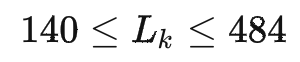
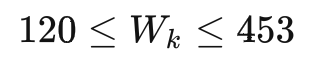
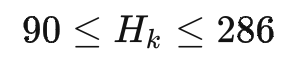
同時我們對sku進行長>寬>高的排序清洗,同時定義紙箱長>寬>高
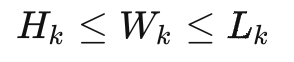 ?
?
最后,我們要求箱子的長寬高數據均為整數,即
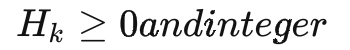
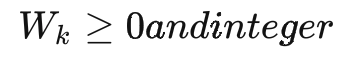
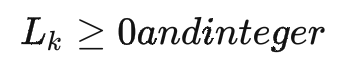
三、優化算法
3.1 一般求解方法概述
對于這個優化問題,通常主要包括精確解算法和啟發式算法:
精確方法主要是用單純形法(線性規劃)或者一些迭代的方法(非線性規劃)再結合分枝定界法找到我們要的整數解。精確方法如果是線性規劃問題能通過單純形法在可行域的頂點中找到全局最優解,非線性規劃也是通過微分學方法或者有限次的迭代找到接近于最優解的,由于不是多項式時間的求解方法,故而往往在大規模實例上不可行。
啟發算法如遺傳算法、蟻群算法、進化算法、智能算法針對普遍的問題。可以將它當作一個黑箱子對幾乎任何問題適用。啟發式算法,說白了就是有方向的窮舉法,在計算資源有限的情況下,需要根據問題場景和模型特點,選擇合理的鄰域結構或操作機制,在全局搜索能力和局部搜索能力之間做權衡。啟發算法通常需要給定初始解;另外,算法不能保證在多項式時間收斂,但常常可以控制算法迭代次數。

3.2 精確解求法
線性規劃
對于線性規劃問題,它的可行解構成的集合為凸集或者無界域,基可行解對應凸集的頂點,通過凸集的性質得出最優解會在凸集的頂點上,然后通過遍歷再排序的方法可以得出最優解,但是當頂點過多的時候,則需要用單純形法找到線性規劃的最優解。
非線性規劃
如果目標函數或者約束條件中含有非線性函數,例如當前的問題中目標函數裝箱率中具有非線性因素,這種規劃問題為非線性規劃問題。一般來說,解非線性規劃問題要比解規劃問題困難的多,它不像求解線性規劃有單純形法這一種通用方法,非線性規劃目前還沒有適用于各種問題的一般算法,各個方法都有自己特定的適用范圍。
整數規劃
因為要求輸出的結果是整數,所以需要用分支定界法來求解。
分支定界法的核心思想就是分枝和剪枝。當不考慮所求解必須是整數這個條件時,用單純形法可求出最優解,但是這個解往往不全是整數,因此采用剪枝的方式一點一點縮小范圍,直到所求解為整數解。
從圖中可以看到,初始化階段,需要給定輸出的全局的上界和下界,如果能有一些啟發式的方法獲得稍微好點的上下界作為初始解導入那是最好的不過的了。如果沒有的話可以先設置為正負無窮大。
接著進入到主循環中,通過求解整數規劃的連續松弛問題(線性規劃)來得到該子問題的上界;分解問題可以幫助對整數規劃問題進行拆分,同時也可以幫助我們得到下界。 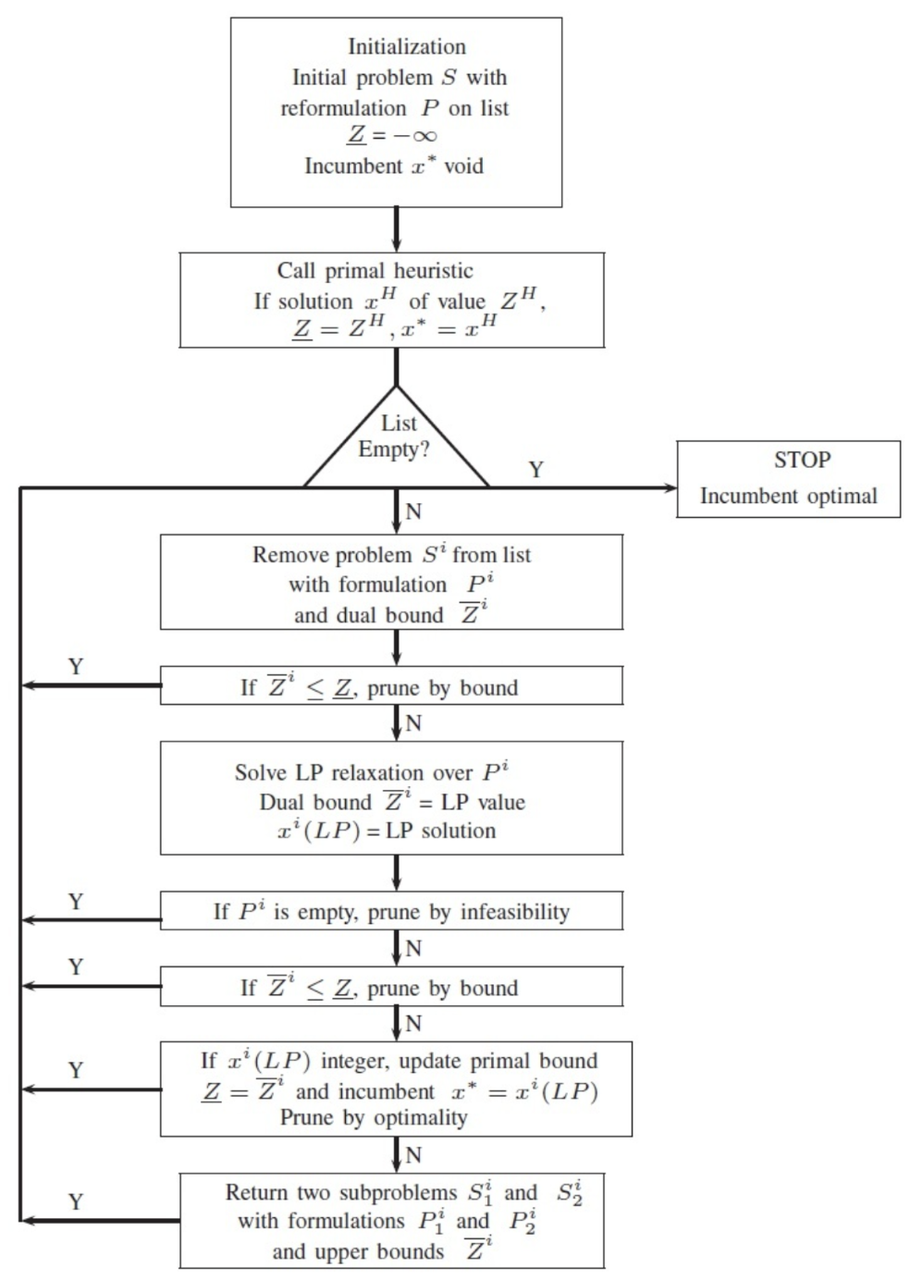
3.3 元啟發式方法
以遺傳算法為代表的這類算法,適合以下場景:
神經網絡超參數優化
一部分結構和特性固定的組合優化問題
一部分機理模型難以建立的黑箱優化問題
多目標優化問題
3.3.1 遺傳算法
基本概念
基因:可行解的元素 染色體:一條染色體為一個可行解 交叉:多條染色體切斷拼接成新的染色體 變異:將染色體的部分基因進行修改 復制:完全遺傳復制上一條染色體
執行流程
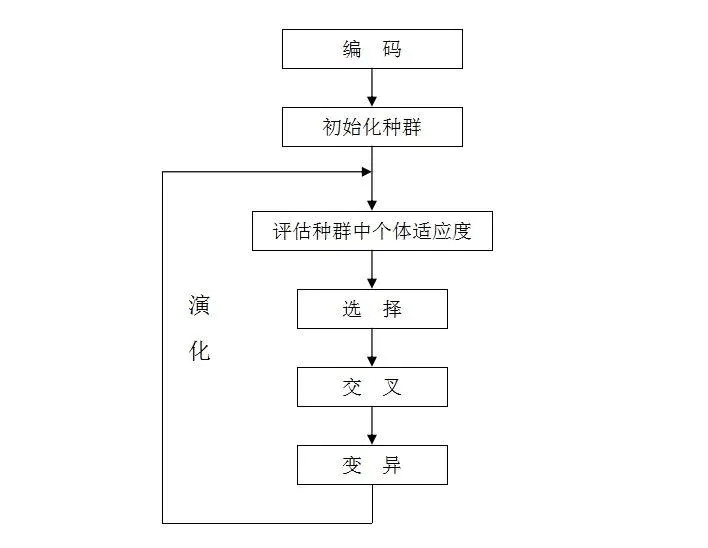
1)在算法初始階段,它會隨機生成一組可行解,也就是第一代染色體。
2)然后采用適應度函數分別計算每一條染色體的適應程度,并根據適應程度計算每一條染色體在下一次進化中被選中的概率。
3)通過“交叉”,生成N-M條染色體。
4)再對交叉后生成的N-M條染色體進行“變異”操作。
5)然后使用“復制”的方式生成M條染色體;
6)重復2~5。
四、具體建模
4.1 數據分析
首先粗略看下近一年得物發貨的sku的長、寬、高主數據及其銷量分布,這是我們設計箱型的依據數據。同時綜合考慮倉內實際作業時候的效率以及采購的成本,因此箱子的種類數量也不可太多,否則會增加倉內打包人員取箱子的難度,采購成本也會相應提高。
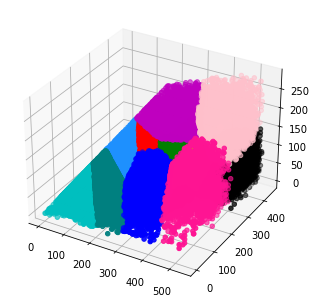
在這一步,考慮到首先要準確和當前箱型 A/B ,同時8~15種這個數量加入到建模參數中也增加了計算復雜度,所以決定固定這個箱型數量的值,首先假設固定N種箱型,每個箱型長寬高三個數,即輸出3 * N個參數。 接下來我們定義一下商品sku和箱型的 長>寬>高,首先對近一年的數據進行長寬高排序、異常值等清洗,例如固定了12種箱型,我們就將sku和箱型在長寬高維度用k-means聚類成12組。
 ? ?
? ?
做這個聚類分析,一方面,根據實際情況,例如結合面單尺寸定義箱型下限,再結合箱型覆蓋率下限值,定義箱型上限尺寸;
另一方面,每個聚類的最大值可以作為箱型的初始化值(實際需要加上5mm作為縫隙)。
4.2 約束和目標
業務上約束來說,只需要將商品裝入箱子,留下縫隙即可,且由于確定箱子的種類數量,這里還需要確定的是每組箱子的長>寬>高,即
constraint_ueq = (
# 單個箱子長>寬>高
lambda x: x[1] - x[0],
lambda x: x[2] - x[1],
lambda x: x[4] - x[3],
lambda x: x[5] - x[4],
...
)
目標則是max 裝箱率,即
def cal_avg_r_cached(p):
'''The objective function. input routine, return total distance.
cal_total_distance(np.arange(num_points))
'''
total_r = 0
for row in npd:
r = [-1] * box_num
for i in range(box_num):
if (row[0] <= p[3 * i]) and (row[1] <= p[3 * i + 1]) and (row[2] <= p[3 * i + 2]):
r[i] = row[4] / (p[3 * i] * p[3 * i + 1] * p[3 * i + 2])
total_r += max(r) * row[3]
print(total_r)
return -total_r / sum_cnt
4.3 結論
最終并行跑了幾個版本,裝箱率均有不等的提升,單均用紙面積有顯著下降; 最終選擇的1203方案作為工程側的輸出,裝箱率提升5.49%,單均用紙面積節約7.6%,單均運費降低0.06元。 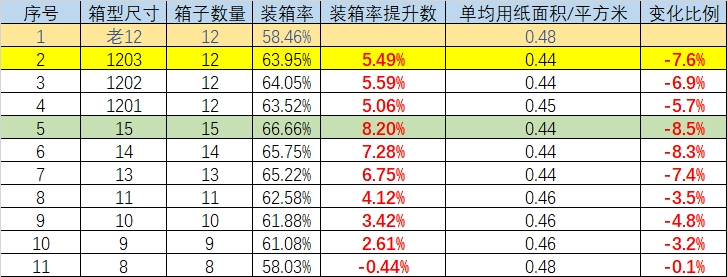
五、彩蛋 -- 使用遺傳算法繪制NONO
在寫這篇文章查相關資料發現的挺有腦洞的內容,用數個帶有顏色的三角形,組裝成圖像。 這里試著用60個三角形繪制了下NONO。
效果大致如下:
 ?
?
在優化算法中,介紹了遺傳算法的大致流程,那么繪制這個NONO和箱型設計有啥區別呢?
在箱型設計中,需要基于裝箱率指標去計算箱子尺寸,因此,在定義適應度函數的時候,只要取Maximize裝箱率這個指標即可,那么到了此處,只要將目標函數定義為不同顏色尺寸的透明三角形組裝結果與目標圖片的相似度即可。
5.1 適應度函數
首先需要找到能夠量化透明三角形組成的圖和目標NONO圖的差異或者相似度的方法,那么如何定義相似度呢?圖像的相似度即在某個顏色空間(例如RGB、HSV)下的值向量的相似度,每個點的差異值總和最小則越接近想要的目標圖案,常用的評估函數例如MSE、RMSE、PSNR、ERGAS、SAM等。
下圖是對于一些圖像噪聲方法,各種相似度評估方法對應的相似度結果。其中“Original”一欄顯示的是原始圖像與自身比較后的分數。 這里選擇ERGAS來作為我們的適應度函數的依據。 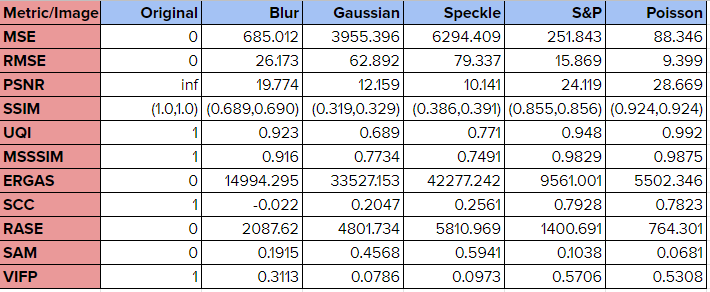
5.2 選擇
這里用不一定完全用輪盤賭方法來做選擇,95%概率選擇適應度函數靠前的解,5%的概率從其他解里面隨機選擇。
if random.random() < 0.95:
'''選擇基因的來源父母,95%幾率從最優的祖先中隨機'''
poly_a = random.choice(polygons[:1])
poly_b = random.choice(polygons[1:5])
else:
'''選擇基因的來源父母,5%從所有的祖先中隨機'''
poly_a = random.choice(polygons)
poly_b = random.choice(polygons)
5.3 交叉和變異
這里也一樣用隨機數,大概率隨機從父類中繼承賦值基因,小概率修改基因值,坐標交叉變異大致如下,顏色交叉變異同理。
temp = random.random() if temp < 1 / polygon_num: '''設定一定幾率坐標變異''' rnd_temp_coord = poly_a.coord_list[i][:] rnd_temp_coord[random.randint(0, vertices - 1)] = random.randint(0, img_width), random.randint(0, img_height) temp_coords.append(rnd_temp_coord) elif temp < 0.5: '''隨機繼承父母中的一個基因''' temp_coords.append(poly_b.coord_list[i]) else: temp_coords.append(poly_a.coord_list[i]) temp = random.random()
審核編輯:劉清
-
RGB
+關注
關注
4文章
798瀏覽量
58547 -
SAM
+關注
關注
0文章
112瀏覽量
33534 -
HSV
+關注
關注
0文章
10瀏覽量
2610
原文標題:得物極光藍紙箱尺寸設計實踐
文章出處:【微信號:OSC開源社區,微信公眾號:OSC開源社區】歡迎添加關注!文章轉載請注明出處。
發布評論請先 登錄
相關推薦
介紹一種 WiMax 雙下變頻 IF 采樣接收機設計方案
解決方案|3D視覺引導多SKU紙箱混拆

求一種POE網口戶外防雷浪涌保護方案
求一種基于PLC的鍋爐爐膛吹灰控制系統設計方案
求一種基于WTR096-28SS芯片方案的寵物喂食器設計方案

求一種基于物聯網的無人智慧藥房系統設計方案

低成本高效率易部署,藍蜂物聯網關+EMCP云平臺賦能工廠數字化轉型
紙箱印刷機PLC數據采集監控運維系統解決方案





 求一種得物極光藍紙箱尺寸設計方案
求一種得物極光藍紙箱尺寸設計方案












評論