作者 |黃杉華東師范大學軟件工程學院博士
蘇亭 華東師范大學軟件工程學院教授
首發 |鑒源論壇 · 觀模
01 什么是隨機測試(Random Testing)
隨機測試是一種使用隨機、相互獨立的程序輸入來對計算機程序進行測試的黑盒軟件測試(在完全忽略程序內部實現細節的情況下進行測試)技術。在處理完隨機且獨立的程序輸入后,程序輸出的結果將會和軟件規格說明(software specifications)中所描述的軟件行為進行比對來判斷該測試是否通過。
隨機測試的核心思想接近于無限猴子定理[1](The Infinite Monkey Theorem),所以隨機測試也被稱為Monkey Testing。無限猴子定理是來自émile Borel的一本出版于1909年的概率相關的書籍,其中描述了這樣一個場景:當一只猴子在打字機鍵盤上不限時間地隨機敲擊,它可能輸出任何給定文章,例如莎士比亞的完整作品,并且這種可能性隨著時間的增長會不斷地接近100% 。換用測試的語言來描述則是測試程序通過不斷地生成測試輸入,其能完整測試整個程序并尋找到程序中異常的可能性會不斷增大。
02早期的隨機測試
最早對隨機測試技術的使用可以追溯到上個世紀五十年代,那時的數據還存儲在穿孔卡片(Punched Card)上。程序員會將扔進垃圾桶中的卡片或者標記有隨機數字的卡組作為計算機程序的輸入來進行隨機測試。
當隨機測試被廣泛認定為測試程序的最差方式時,Duran和Ntafos兩人在1981年正式地對使用隨機測試技術對程序進行測試的有效性進行了調研,結果表明相對于系統化的測試技術,隨機測試是一個成本低收益高的替代品。
后來在1983年,蘋果公司的Steve Capps開發了一款名為“The Monkey”的隨機輸入生成工具用來對傳統的MacOS應用進行測試。他對工具的命名就是化用了無限猴子定理。
1991年,一款名叫 “crashme” 的工具發布。這款工具意在通過隨機執行帶有隨機參數的系統調用來測試Unix以及類Unix操作系統的魯棒性。
03隨機測試的優缺點
3.1 優點
(1)容易實現和使用。隨機測試并不需要知曉程序細節,并且輸入也通過隨機生成。
(2)對程序不存在偏見。由于隨機測試的輸入都是隨機生成的,不存在人為因素影響,也就不會因為對程序某一部分信任而忽略掉潛在的漏洞。
(3)能快速查找漏洞。隨機測試的測試速度快,通過快速和大量的測試,能夠在短時間內找到大量的候選漏洞(對漏洞的確認還需要人工參與)。
3.2 缺點
(1)尋找漏洞的精度不高。由于隨機測試的完全隨機性,尋找到的漏洞很可能是一些無關緊要的錯誤。
(2)過于隨機導致對程序的代碼覆蓋率不高。大部分人認為對程序的測試過于依賴隨機,不如通過人工白盒測試的方式來更精確地測試程序。
04隨機測試進階—模糊測試(Fuzzing)
在1988年的一個風雨交加的夜晚,威斯康星大學的Barton Miller教授在自己的公寓中通過一條電話線連接他在學校中的計算機。暴風雨引發了電話線中的信號錯亂,以至于所連接的Unix終端不斷接收到糟糕的命令輸入,最終導致了系統崩潰。頻發的崩潰使這位講授操作系統課程的教授感到驚訝,因此他腦海中浮現了一個對Unix系統進行魯棒性測試的念頭。于是他在給學生的課程作業中寫道:
The goal of this project is to evaluate the robustness of various UNIX utility programs, given an unpredictable input stream. This project has two parts. First, you will build a fuzz generator... Second, you will take the fuzz generator and use it to attack as many UNIX utilities as possible, with the goal of trying to break them... [2]
教授在作業中要求學生開發一個模糊生成器(fuzz generator),這個生成器可以產生不可預測的輸入流,然后將這些雜亂的輸入給到Unix系統設施,然后試圖攻陷這些設施并找到和分析引發錯誤的隨機輸入和原因。這就是模糊測試的誕生,教授在作業中使用的fuzz一詞也就被用來命名這一技術。
從上文可以看到模糊測試在誕生之初和隨機測試十分相似,都是通過隨機的輸入來對計算機程序進行功能行為測試。下面的Python代碼片段給出了一個最簡單的模糊器(fuzzer)例子。這個模糊測試器接收三個參數:最大長度(max_length)、字符的ASCII碼起始值(char_start)以及字符的ASCII碼從起始到結束的范圍(char_range)。該模糊器將生成一個長度為max_length的包含ASCII碼在[char_start, char_start + char_range)范圍內的字符串。

圖 1
所以最原始的模糊測試和隨機測試擁有相同的優缺點。其中最顯著的問題就是由于其完全的隨機性,尋找到的程序錯誤過于刁鉆。可能找到的程序錯誤只是因為錯誤的輸入導致而和程序本身實現無關,或者程序使用人員根本就不會使用像模糊測試器生成的輸入,所以不會在軟件設計的考慮范疇之內,甚至模糊測試根本就沒有測試到程序的主要功能。
無論如何模糊測試還是有其可取之處的(尤其是測試速度快、易于實現),所以后來的研究者們不斷想方設法地,尤其是針對如何更好地生成測試輸入方面去提高模糊測試的精度(找到的錯誤確實是和軟件規范說明或預期設想行為不符)和深度(能更多地去測試程序的主要功能)來完善模糊測試的實用性。實現這些目標的主要方法就是通過一些靜態(基于覆蓋率、基于變異)或動態(基于搜索、基于語法)的方式給模糊器提供額外的輔助信息來幫助模糊器更高效地生成、更有效地測試輸入,而不再是完全隨機,這也促使模糊測試從黑盒測試向灰盒測試進行轉變。下文會進行具體介紹。
現在的模糊測試技術可以有幾種劃分方式(不限于此):
·一種模糊測試技術可以是基于生成(generation-based)的或者基于變異(mutation-based),取決于它是在沒有任何參考的情況下生成隨機輸入,還是在現有輸入的基礎上進行修改,也就是所謂的變異;
·一種模糊測試技術可以是愚笨的(dumb)或者聰明的(smart),取決于它是否對測試輸入的結構敏感;
·一種測試技術可以是白盒、灰盒或者黑盒(基本上不再使用),取決于它是否對程序結構信息或者程序運行信息敏感。
目前最流行的模糊測試工具主要有AFL以及AFL的擴展系列,如AFLFast、AFL++、AFLGo等。
4.1基于覆蓋率的模糊測試(Coverage-Based Fuzzing)
對于如何提高模糊測試精度和深度的探索,其中一種是利用了代碼覆蓋率[3](code coverage)這一概念。代碼覆蓋率包括函數覆蓋率(function coverage)、語句覆蓋率(statement coverage)、邊覆蓋率(edge coverage)以及條件覆蓋(condition coverage)率等多種覆蓋準則,這些覆蓋率都在一定程度上反映了測試用例對于程序代碼的測試程度,即代碼覆蓋率越高,測試用例對代碼的測試程度越高。近期的一項工作[4]也觀察到模糊測試技術的代碼覆蓋率和能找到程序中的錯誤具有強相關性。
下面的Python代碼片段將給出簡單的例子。當輸入inp為一個正數的時候,程序執行過程中將會執行第 2 行和第 3 行的代碼語句,則語句覆蓋率為 2 / 6 = 33.3%。另外對于條件覆蓋率來說,整個函數中函數有三個 if 條件語句,每一個 if 條件語句都有真假兩種情況,則根據組合原理該函數共有 6 個條件分支。在上述情況下,程序執行過程中只有第一個 if 條件語句為真的分支被執行,則條件覆蓋為 1 / 6 = 16.7%。對于輸入 inp 為零和負數的情況,語句覆蓋為 3 / 6 = 50% 和 4 / 6 = 66.7%,條件覆蓋率為 2 / 6 = 33.3% 和 3 / 6 = 50%。

圖 2
在模糊測試中對于覆蓋率的利用,主要是在測試用例的生成過程中。模糊器首先生成一定個數的隨機輸入,這些輸入被稱為種子(seed)。接著模糊器將這些種子輸入程序,回收程序執行的結果和預先選定的覆蓋率指標。接下來模糊器會根據覆蓋率高低,將覆蓋率低的種子丟棄,將覆蓋率高的種子保留并對這些種子進行操作生成一批新種子再作為輸入運行程序。重復上述過程到覆蓋率不能夠更進一步提高時,終止測試。
4.2 基于變異的模糊測試(Mutation-Based Fuzzing)
由于最初的模糊器完全靠隨機生成程序輸入,模糊測試很難生成出符合程序要求的合法輸入,以至于很難測試到程序的核心功能,同時這也是代碼覆蓋率極低的一個原因。于是基于變異的模糊測試被提出來解決這個問題。
變異的核心思想是對現有的種子(種子可以合法也可以不合法,但大多數情況下會使用合法的種子,這樣通過變異得到的種子后代質量較高)以及通過變異得到種子后代進行操作來生成測試輸入。具體的變異操作需要測試人員執行制定。假如針對一個計算機程序的一個合法的程序輸入為“3+0”,那么在指定變異操作為隨機增加、刪除和替換字符串中的某一個字符這三種操作時,經過變異之后的輸入就有多種可能,如“3 + - 0”、“3 +”、“3 / 0”。將這些通過變異得到的種子后代扔入程序中運行,這就是基于變異的模糊測試。
變異操作可以被設計為更加復雜精細的過程,例如結合其他種子質量評估指標進行變異或者進行某種針對性變異操作。上一小節末尾描述的將變異操作和覆蓋率指標進行結合來反復對程序進行測試,這樣可以很好地利用這兩種方法的優勢,從而增強模糊測試的有效性。著名的模糊測試工具AFL就是基于這樣的思路開發的。
4.3基于搜索的模糊測試(Search-Based Fuzzing)
基于搜索的模糊測試主要依賴于搜索算法。搜索算法也被稱為啟發式算法(heuristic algorithm),其核心思想是通過某些程序信息來啟發和引導算法執行。這些算法的靈感大多是來自自然界的現象,如模擬退火算法和本小節會介紹的遺傳算法。而它們之所以被稱為搜索算法,是因為執行這些算法可以在較大的搜索空間中比隨機算法或遍歷算法更高效。同樣以上一小節的計算機程序輸入為例,模糊器對該程序進行模糊測試本質上就是在不斷地探索其輸入空間,該輸入空間中包含了任意長度的合法或不合法的表示四則運算表達式的字符串。想要通過測試來挖掘出程序中隱藏的缺陷,就是在輸入空間中搜索到特定的輸入使得該程序在運行時出現異常行為;想要滿足更廣的程序覆蓋率,就是在輸入空間中搜索到特定的輸入使得讓該程序運行時執行更多的程序語句。
因此搜索算法也就自然而然地與模糊測試結合在了一起,來使模糊器生成更優質的程序測試輸入。下面將對基于結合代碼覆蓋率的遺傳算法的模糊測試進行簡單的介紹。
我們構建一個簡單函數 fun2,該函數將判斷特定字符是否存在于輸入字符串中,然后對應分支返回一個整型數字。

圖 3
在這個例子中我們給定模糊器的初始種子,為“axxx”,“xxxb”、“xxxc”和“xxxd”。我們首先將這些種子作為輸入來運行這個函數,得到每個種子的語句覆蓋數量,分別是 3 、2 、2、2 。輸入“axxx”是可以讓程序執行第 2、3 和 8 行語句,而后三個輸入只能執行第 2 和 8 行語句。第一輪測試已經結束,這時我們根據種子的語句覆蓋數量來生成下一次測試輸入集合,具體過程為從種子中選取語句覆蓋數量最多的兩個作為親代來進行交叉變異(模擬自然界的遺傳現象)。由于后三個種子的數據覆蓋數量都為 2 ,則在選擇時會隨機選取。假設“axxx”和“xxxb”得到了選擇,則繼續對這兩個種子進行交叉變異,此處交叉變異定義為交換兩個種子的右半部分子串,即得到的子代為“axxb”和“xxxx”。重復這樣的選擇并交叉變異的過程直到子代數量等于初始種子數量。假定經過上述過程我們最后得到了“axxb”、“xxxx”、“axxc”和“xxxx”這四個子代,然后就繼續重復整個執行過程,也就是將這些子代輸入程序繼續運行遺傳算法來生成更加優質的測試輸入,最終提高代碼覆蓋率和異常檢測能力。
從上述例子中可以看到在子代中的“axxb”不僅將原本“axxx”的語句覆蓋數量從 3 提升到了 4,并且能更深入地探索整個函數中的條件分支。但可以看到對于上述例子中假設得到子代整個算法已經無法再有進步了,因為這些子代不論怎么交叉變異也無法得到一個包含abc三個字母的字符串。在實際工業生產環境中算法本身會更加復雜,測試種子會經過精心生成和挑選,同時納入更多指標進行算法引導,對交叉變異的過程也不會只是簡單地字符串交換。
4.4 通過文法進行模糊測試(Fuzzing with Grammars)
當程序的輸入具有一定規范和結構的(比如數據庫或者API的輸入),人們開始嘗試通過文法(Grammar)來幫助模糊器生成合法規范的測試輸入,屬于前面提到的基于生成(Generation-based)的模糊測試技術。
下面展示了一個簡單的文法,該文法描述的是含有小數或整數的加減乘除的四則運算表達式,如 (1 + 2) * (3.4 / 5.6 - 789) 。使用該文法,從 非終止符(non-terminal)開始展開,最終就可以得到一個可用于測試計算程序的合法的四則運算表達式。

圖 4
對于表達式 (1 + 2) * 3 的部分推導過程如下,過程中遵循最左推導。推導中剩下的部分讀者可以自行嘗試完成。

圖 5
通過這樣來產生測試輸入相比于純隨機的方式不僅產生的種子質量高,并且符合程序輸入規范,能夠節省無效測試用例的時間開銷從而提高測試效率。
05總結
隨機測試為軟件測試提供了一個在黑盒情況下快速和大量地測試程序的全新思路,其進階版模糊測試更是在經過包括上述基于覆蓋率、基于變異、基于搜索以及文法輔助在內的多種方法的增強之后,成為了當前工業環境下軟件測試的主流選擇,被廣泛應用于人工智能測試、自動駕駛系統測試、數據庫系統測試、API測試等各種測試場景。雖然克服了隨機測試和模糊測試誕生之初的缺陷和問題,當下的模糊測試仍然有待提高進步,例如對模糊測試過程中對觸發的程序錯誤的類型進行識別、整理和分類,以及對引發錯誤的根源誘因的分析等。學界和工業界也對傳統靜態分析工具如符號執行技術和模糊測試技術相結合的道路在不斷地探索。
參考資料:
[1]“Infinite Monkey Theorem.” In Wikipedia, September 1, 2022.
[2] Bart Miller. 1988. [3] “Code Coverage.” In Wikipedia, July 7, 2022.
[4] Marcel B?hme, László Szekeres, and Jonathan Metzman. 2022. On the reliability of coverage-based fuzzer benchmarking. In Proceedings of the 44th International Conference on Software Engineering (ICSE '22). Association for Computing Machinery, New York, NY, USA, 1621–1633.
[5] “The Fuzzing Book.” Accessed November 5, 2022.
審核編輯 黃昊宇
-
軟件測試
+關注
關注
2文章
231瀏覽量
18623
發布評論請先 登錄
相關推薦
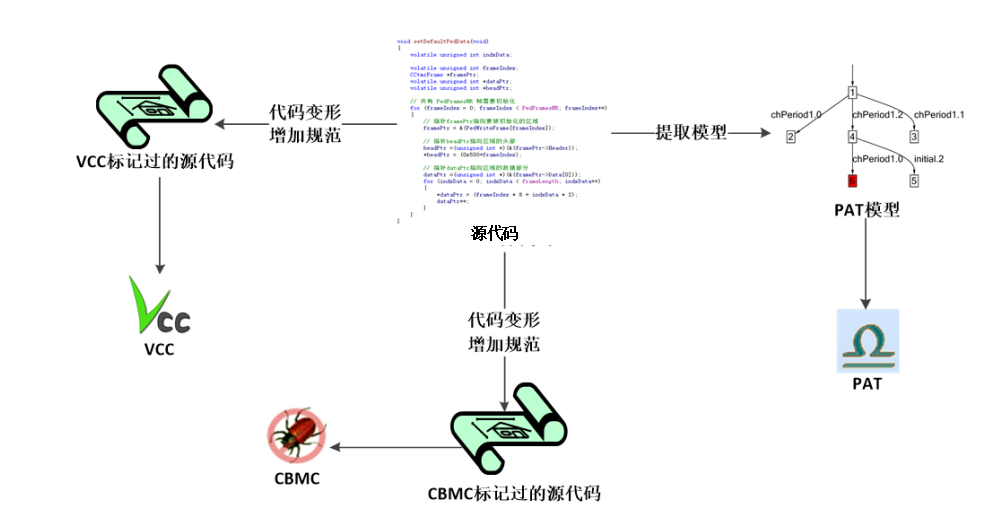
鑒源論壇 · 觀模丨形式化驗證——以操作系統任務調度算法驗證為案例
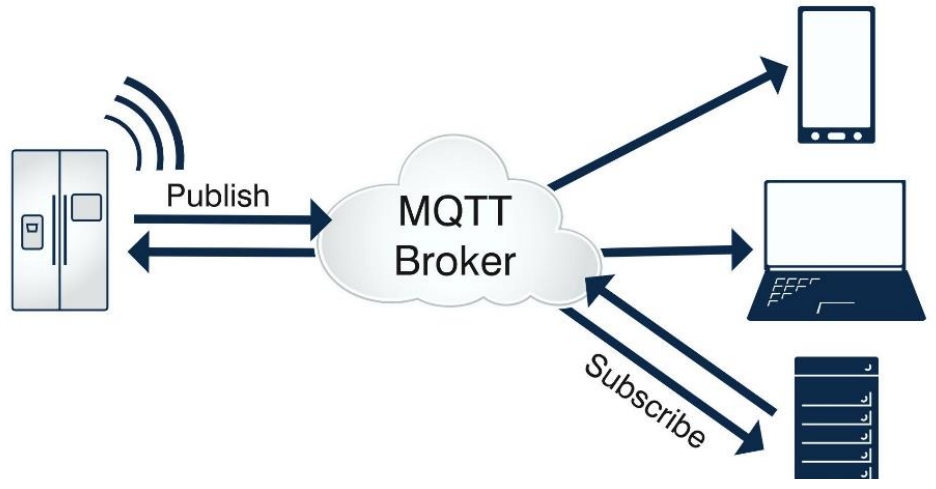
鑒源實驗室·基于MQTT協議的模糊測試研究
鑒鷹電子仿真設計大賽——單片機高手打造之旅
【金鑒出品】“七問七答” 解開雷擊浪涌之謎!
助推在線教育技術創新 VIPKID宏恩觀技術分享論壇面世
鑒源論壇 · 觀模丨基于搜索的測試生成
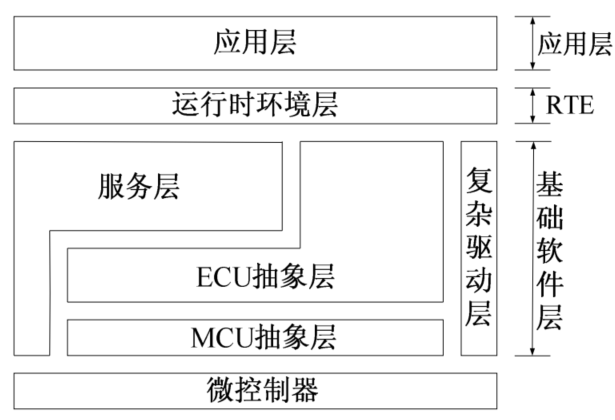
鑒源論壇 · 觀模丨基于AUTOSAR的TTCAN通信協議的形式化建模與分析
君鑒科技受邀參加2023中關村論壇

鑒源實驗室丨智能網聯汽車協議模糊測試技術概述
鑒源實驗室丨汽車入侵檢測系統介紹及測試




 鑒源論壇 · 觀模丨淺談隨機測試
鑒源論壇 · 觀模丨淺談隨機測試










評論