本文討論了信號經過傅立葉變換所得頻譜的物理意義,其中著重于負頻率成分。許多信號與系統的教材中,都認為負頻率成分沒有物理意義。本文以多方面的實例證明了負頻率成分不但具有明確的物理意義,而且有重要的工程應用價值。文章還用Matlab程序演示了如何用幾何方法求傅立葉反變換,把集總頻譜合成為時域信號,從中也可鮮明地看出負頻率成分的意義。
1 負頻率與復信號
頻率的原始定義是每秒出現的次數,可用以衡量機械運動、電信號、乃至任何事件重復出現的頻度,這當然不存在有“負”的概念。當用頻率描述圓周運動時(即進入了二維信號平面),產生了角頻率ω的概念。從機械旋轉運動出發,ω=dθdt定義為角速度。對于周期運動,角速度也就是角頻率。通常以逆時針為正,因此轉動的正頻率是逆時針旋轉角速度,負頻率就是順時針旋轉角速度。正號和負號是非常自然形成的,不存在有無物理意義的問題。
電的單位向量(電壓或電流)圍繞原點的轉動,可以用0 表示,這是在電路中都清楚的。θ的正負所代表的物理意義從來沒有什么爭議,它的導數ω=dθ/dt的物理意義不言自明。取正取負都不影響定義,為什么取負就會失去物理意義了呢?
在信號與系統課程中為簡化問題,便于初學者掌握概念,開宗明義地把研究范圍限定于實信號f(t),也就是在電壓旋轉向量)中,只研究它在實平面或虛平面上的一個投影sin(ωt)或cos(ωt),研究復信號 ejωt的特性與只研究實信號sin(ωt)或cos(ωt)是兩個不同的層次。前者(復信號)是反映信號在空間的全面特性,如圖1所示。后者(實信號)只研究了信號在一個平面(x-t或y-t組成的平面)上投影的特性。這就必然要丟掉一些重要的信息,以致x=sin(ωt)與sin(?ωt)在z-t平面中的波形沒有任何差別,這是人們對負頻率的意義產生疑問的直接原因之一。很顯然,在x-t 或y-t的平面內,是不可能看出旋轉的。既看不到θ ,也看不到ω 。只有在x-y平面上才能看到這兩個旋轉參數。
注意上述所說的x平面對應實部 ,y平面對應虛部,也就是說此文章是站立在復數表示已經有相應的物理意義的前提下進行的討論,那么我先給了j一個有效的理論支持,電路理論中 j,-j,-1, 都可以看成是旋轉因子。復數 F 乘以j,相當于 F 在復平面中逆時針旋轉90度 ;復數 F 乘以 -j,相當于順時針旋轉 90度;F 乘以或除以 -1, 相當于 F 順時針或逆時針旋轉180度
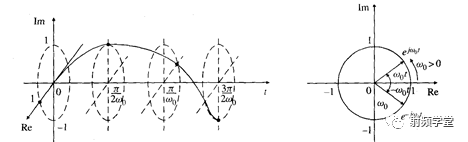
圖1 復信號ejωt
2 復信號與實信號的頻譜
同樣,用 ejωt、sin(ωt)或cos(ωt)作為核來做傅立葉變換所得的結果也是復信號全面,實信號片面。對實信號做傅立葉變換時,如果用指數ejωt為核,將得到雙邊頻譜。以角頻率為n的余弦信號為例,它有具有位于±n兩處的、幅度各為0.5、相角為零的頻率特性。它的幾何關系可以用圖2表示。兩個長度為0.5的向量:分別以士n等速轉動,它們的合成向量就是沿實軸方向酌余弦向量 簡沿虛軸方向的信號為零。可見必須有負頻率的向量存在,才可能構成純粹的實信號。所以歐拉公式)
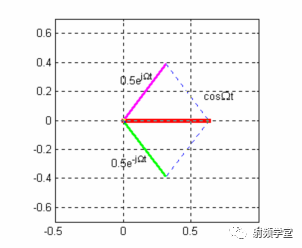
圖2 實數信號由正負頻率復向量合成
4)多普勒頻率
多普勒頻率又是一個負頻率的實例,如果信號的發射源向我們運動而來,那么多普勒頻率就是正頻率;如果信號的發射源向我們遠離而去,那么多普勒頻率就是負頻率,在這里正負頻率都是有明確物理意義的。多普勒頻率雖是一種差頻,它表現為合成信號的包絡頻率,因此仍然符合上述的原理,在實信號域只能求出多普勒頻率的大小,但檢測不出它的正負。要得到負頻率,必須從復信號域考慮。可見,不懂得這一點,就無法找到多普勒測速的原理框圖。
歸根到底,轉角和頻率的正負,必須在x-y平面或二維信號中才能觀察到。因為觀察的方法不對,看不到其意義,從而否認它的存在,這是認識論上的錯誤,不是科學的方法。這就和“瞎子摸象”的故事所說的那樣,摸象腿的人否認象有鼻子,毛病出在他的驗證方法。他老想在象腿(實信號域)上找到象鼻子(負頻率),當然也永遠找不到。正確的方法是必須換一個角度,摸別的部位(復信號域),才能得到全面的知識。
某些學者不承認負頻率是由于把“頻率是每秒鐘循環的次數”的陳舊概念絕對化,其實頻率的概念是不斷發展充實的。每秒次數的概念只能粗糙地研究信號外部形態,無法涉及信號每周期內部的細微波形特征,而這恰好是傅立葉變換的任務。從它的核已經可以清楚地看到,正是它摒棄(或發展)了原始的頻率定義,采用了角頻率的概念。單位是弧度/秒,而且具有明確的方向和正負號。其實頻率的概念還在繼續發展,進入到數字信號處理時又進一步出現了數字頻率,它的單位是弧度(去掉了分母上的“秒”),取值范圍是[-π,π]。它的物理意義已變為兩次采樣時刻之間向量轉過的角度,在文獻[1]中對此有詳細的說明。如果停留在“每秒次數”的舊概念上,那“數字信號處理”也就無法發展了。
5.從認識論角度糾正對負頻率的錯誤說法
這個問題是從教學中提出的,作者在旁聽“信號與系統”課程時,在老師的幻燈片上看到了“關于雙邊譜,負頻率只有數學意義,沒有物理意義”的提法。我們覺得這是個錯誤,而且恐怕不是個別老師的想法。回來一查,果然如此,很多相當權威的主流教材上都這么寫。
其實,“×××只有數學意義,沒有物理意義”這樣的“命題”誰也沒有證明過,也是無法證明的,它最多只能算是猜想。只要有一個反例就可被推翻,本文已經舉出了多個反例,說明它是完全錯誤的。教師絕不該把錯誤的猜想說成真理,更不能寫在書上和幻燈片上去誤導學生。數學是更抽象、更深刻地描述物理現象的工具,而物理是實證的科學。限于條件,人們往往暫時還認識不到數學定理的物理意義。數學超前物理是科學史上多次出現的現象,比如虛數、非歐氏幾何等。這時應該努力去理解它,認識它,而不是輕易地放棄它、否定它。自己沒想通,沒找到的事物,不能說它不存在。給學生講課時,只能說“我們目前還沒有想通×××的物理意義”。這才能表明教師在科學上的嚴肅和謙遜,也有助于培養學生的科學鉆研和創新精神。
6.結束語
討論這個問題,不僅是理論上的探討,對于提高教學質量是有重大意義的。今天,信息技術如此的發展,很大程度是由于深入大量地開發頻譜資源的結果。在同學剛進入這個資源庫的時候,我們要引導他們對這個寶藏發生極大的興趣,非常珍惜這個寶藏,去深鉆,去挖掘它的每一點潛力。不能為了省事,為了堵住學生的好奇提問,輕率地、毫無根據地一句話就把頻譜的負頻率半邊扔掉了。在入門的時候,當然不可能把本文說的概念統統灌輸給學生,要順序漸進。但老師首先要有更寬廣的知識面和更科學的思維方法,教出的學生的才會具備更多的想象力和創造性。
審核編輯:郭婷
-
matlab
+關注
關注
185文章
2979瀏覽量
230723 -
電壓
+關注
關注
45文章
5622瀏覽量
116021
原文標題:論頻譜中負頻率的物理意義
文章出處:【微信號:射頻學堂,微信公眾號:射頻學堂】歡迎添加關注!文章轉載請注明出處。
發布評論請先 登錄
相關推薦
傅立葉變換在機器學習中的應用 常見傅立葉變換的誤區解析
傅立葉變換與時域信號的關系 傅立葉變換在音頻信號處理中的應用
如何使用傅立葉變換進行頻譜分析
傅立葉變換的基本概念 傅立葉變換在信號處理中的應用
傅里葉變換在信號處理中的應用
無線通信頻譜分析儀的技術原理和應用場景
信號判別波形頻譜的方法有哪些
幅頻特性和相頻特性的具體物理意義是什么?
如何使用SBench 6對數字化儀采集信號進行處理?(三)——快速傅立葉變換(FFT)




 信號經過傅立葉變換所得頻譜的物理意義討論
信號經過傅立葉變換所得頻譜的物理意義討論











評論