時域信號
時域上,電信號的幅度是隨著時間變化的。其圖形,是示波器常用的顯示模式。
同時,也可以用矢量投影來表示隨時間變化的波形。
這兩種顯示模式之間的關系,如下圖所示,可以通過一個簡單的正弦信號顯示出來。
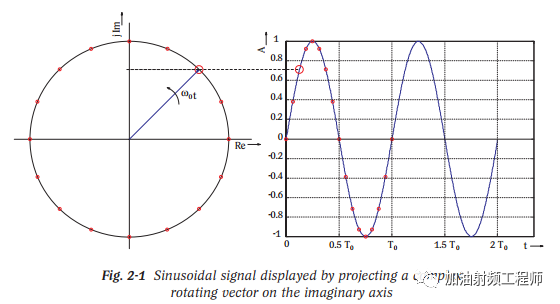
時間軸上的振幅對應于投影在虛軸上的矢量分量,即:
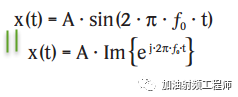
矢量的角頻率可以由下式得到:

時域和頻域信號的關系
時域和頻域這兩種表示形式,可以通過傅里葉變換相互關聯。
所以時域中的每一個信號都在頻域中對應相應的頻譜。
傅里葉變換公式,如下圖所示。

周期信號
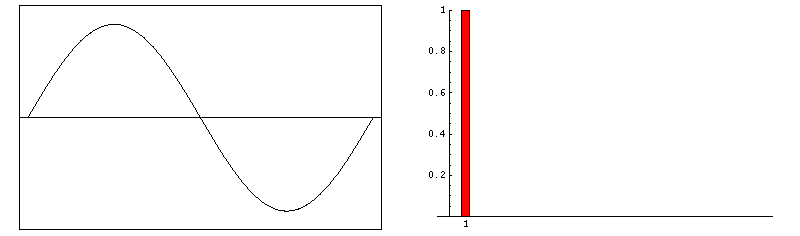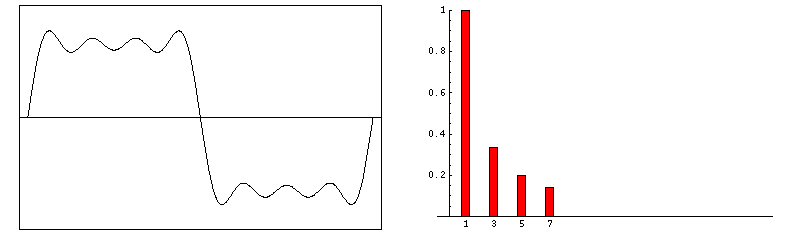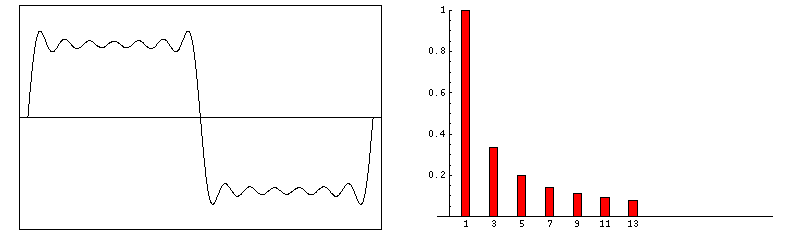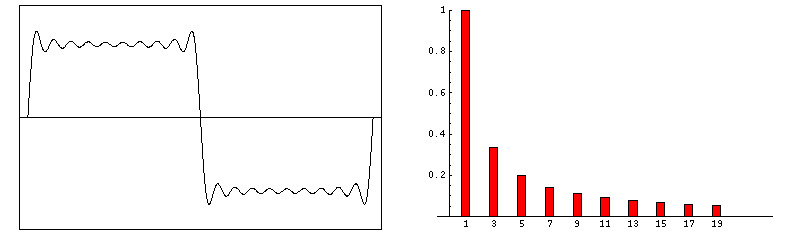
根據傅里葉定理,任何時間域中的周期性信號都可以分解為不同頻率和振幅的正弦/余弦信號的總和。這樣的總和被稱為傅里葉級數。如下圖所示:

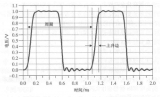
下圖表示了,傅里葉級數前四項之和。
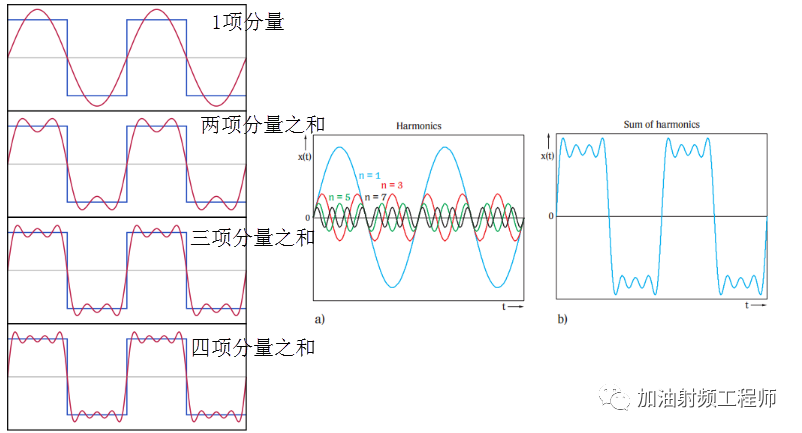
當諧波數量增多時,信號就越接近于理想的矩形脈沖。
當信號為余弦信號時,其頻譜為:
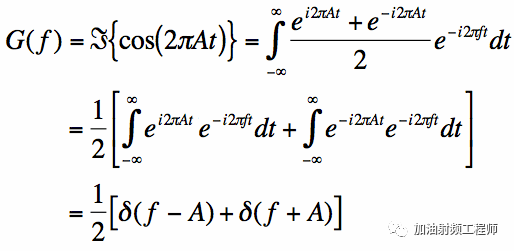
當信號為正弦信號時,其頻譜為:
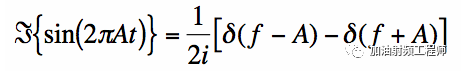
可以看出,正弦和余弦信號的頻譜都由狄拉克脈沖組成,而且他們的傅里葉變換在幅度上是相同的,因此這兩個信號在同一頻率處表現出相同的幅度譜。
一個周期性信號的頻譜,可以用傅里葉級數來表示。級數中的每一個分量,在頻域都對應一個迪拉克脈沖,它是頻域中的一個離散分量。因此,周期性信號總是表現出離散頻譜,也被稱為線譜。
下圖是近似矩形信號對應的時域分量和頻域分量。
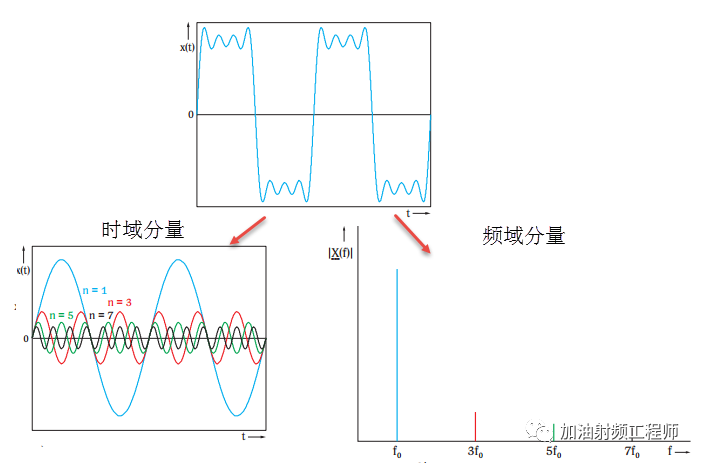
下圖是一些周期信號在時域和頻域的表示。
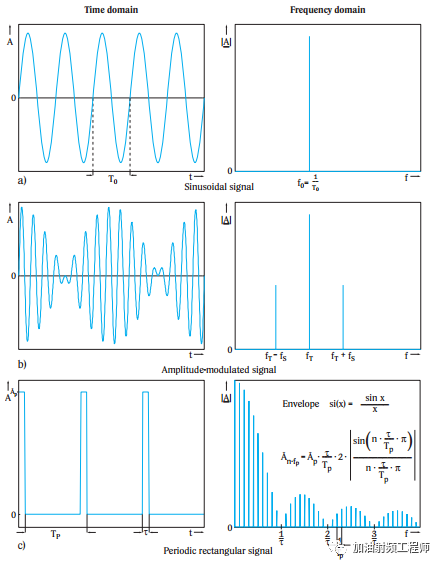
非周期信號
那周期信號可以用傅里葉級數來表示,但是非周期信號呢?
非周期信號的頻譜可以通過傅里葉變換來計算,其頻譜不是由離散頻譜分量組成的。非周期信號在頻域為連續頻譜,其頻譜密度與頻率有關。
與正弦和余弦信號類似,對于許多信號來說,都能獲得確切的表達式。
但對于在時域具有隨機特性的信號,如噪聲或隨機比特序列,則很少能得到相應的頻域解。在這種情況下,頻譜可以則一般通過數值解來確定。
下圖中是一些非周期信號在時域和頻域的表示。
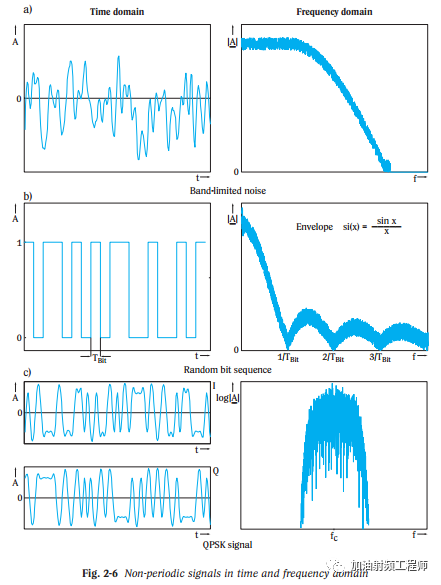
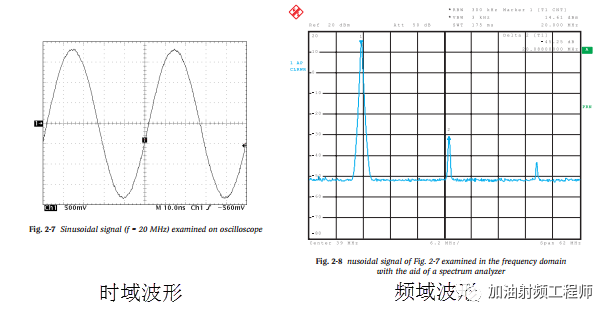
當要看時域波形時,可以用示波器進行測量;當要看頻域波形時,可以用頻譜儀進行測量。
下圖所示的信號似乎是一個頻率為20MHz的純正弦波信號。同樣,大家也期望在頻域,只有20MHz的單根頻譜。
但是,借助頻譜分析儀在頻域中檢查該信號時,發現除了基波之外,還有幾個高階諧波。所以,諧波分量則在時域中看不出來。
審核編輯:湯梓紅
-
示波器
+關注
關注
113文章
6260瀏覽量
185182 -
信號
+關注
關注
11文章
2791瀏覽量
76835 -
時域
+關注
關注
1文章
71瀏覽量
28540 -
頻域
+關注
關注
1文章
87瀏覽量
26307
原文標題:信號的兩種表現形式-時域和頻域
文章出處:【微信號:加油射頻工程師,微信公眾號:加油射頻工程師】歡迎添加關注!文章轉載請注明出處。
發布評論請先 登錄
相關推薦
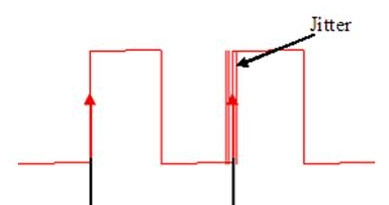
時鐘抖動和相噪及其測量方法




 信號的兩種表現形式-時域和頻域
信號的兩種表現形式-時域和頻域











評論