1
點云配準過程就是求一個兩個點云之間的旋轉平移矩陣(rigid transform or euclidean transform 剛性變換或歐式變換),將源點云(source cloud)變換到目標點云(target cloud)相同的坐標系下。 可以表示為以下的方程:  其中
其中
 就是target cloud與source cloud中的一對對應點。 而我們要求的就是其中的R與T旋轉平移矩陣。 這里,我們并不知道兩個點集中點的對應關系。這也就是配準的核心問題。
就是target cloud與source cloud中的一對對應點。 而我們要求的就是其中的R與T旋轉平移矩陣。 這里,我們并不知道兩個點集中點的對應關系。這也就是配準的核心問題。
2
配準分為粗配準與精配準兩步粗配準就是再兩個點云還差得十萬八千里、完全不清楚兩個點云的相對位置關系的情況下,找到一個這兩個點云近似的旋轉平移矩陣(不一定很精確,但是已經大概是對的了)。 精配準就是在已知一個旋轉平移的初值的情況下(這個初值大概已經是正確的了),進一步計算得到更加精確的旋轉平移矩陣。 這里從精配準開始講起。 精配準的模式基本上已經固定為使用ICP算法及其各種變種。ICP算法由Besl and McKay 1992, Method for registration of 3-D shapes文章提出。 文中提到的算法不僅僅考慮了點集與點集之間的配準,還有點集到模型、模型到模型的配準等。 簡要介紹一下點集到點集ICP配準的算法:1) ICP算法核心是最小化一個目標函數:

(這里的表述與原文略微有些不同,原文是用四元數加上一個偏移向量來表達旋轉平移變換。) 就是一對對應點,總共有
就是一對對應點,總共有 對對應點。這個目標函數實際上就是所有對應點之間的歐式距離的平方和。2) 尋找對應點可是,我們現在并不知道有哪些對應點。因此,我們在有初值的情況下,假設用初始的旋轉平移矩陣對source cloud進行變換,得到的一個變換后的點云。 然后將這個變換后的點云與target cloud進行比較,只要兩個點云中存在距離小于一定閾值(這就是題主所說的ICP中的一個參數),我們就認為這兩個點就是對應點。這也是"最鄰近點"這個說法的來源。3) R、T優化有了對應點之后,我們就可以用對應點對旋轉R與平移T進行估計。這里R和T中只有6個自由度,而我們的對應點數量是龐大的(存在多余觀測值)。因此,我們可以采用最小二乘等方法求解最優的旋轉平移矩陣。一個數值優化問題,這里就不詳細講了。4) 迭代我們優化得到了一個新的R與T,導致了一些點轉換后的位置發生變化,一些最鄰近點對也相應的發生了變化。 因此,我們又回到了步驟2)中的尋找最鄰近點方法。2)3)步驟不停迭代進行,直到滿足一些迭代終止條件,如R、T的變化量小于一定值,或者上述目標函數的變化小于一定值,或者鄰近點對不再變化等。(這里也是題主所說的ICP算法中的一個參數) 算法大致流程就是上面這樣。這里的優化過程是一個貪心的策略。首先固定R跟T利用最鄰近算法找到最優的點對,然后固定最優的點對來優化R和T,依次反復迭代進行。 這兩個步驟都使得目標函數值下降,所以ICP算法總是收斂的,這也就是原文中收斂性的證明過程。這種優化思想與K均值聚類的優化思想非常相似,固定類中心優化每個點的類別,固定每個點的類別優化類中心。 關于參數的選擇: ICP算法的參數主要有兩個。一個是ICP的鄰近距離,另外一個是迭代的終止條件。這些參數的選擇,與實際的工程應用相關。比如說你的儀器精度是5mm,那么小于5mm是可以認為是對應點,而最終的迭代終止條件也就是匹配點之間平均距離小于5mm。 而且這些參數可以由算法逐步迭代減小,最初使用較大的對應點距離參數,然后逐步減小到一個較小的值。(問過師兄才知道實際過程這樣操作會比較合適。)需要手動調整一些參數。(這跟機器學習調參比起來,簡直不是事~)
對對應點。這個目標函數實際上就是所有對應點之間的歐式距離的平方和。2) 尋找對應點可是,我們現在并不知道有哪些對應點。因此,我們在有初值的情況下,假設用初始的旋轉平移矩陣對source cloud進行變換,得到的一個變換后的點云。 然后將這個變換后的點云與target cloud進行比較,只要兩個點云中存在距離小于一定閾值(這就是題主所說的ICP中的一個參數),我們就認為這兩個點就是對應點。這也是"最鄰近點"這個說法的來源。3) R、T優化有了對應點之后,我們就可以用對應點對旋轉R與平移T進行估計。這里R和T中只有6個自由度,而我們的對應點數量是龐大的(存在多余觀測值)。因此,我們可以采用最小二乘等方法求解最優的旋轉平移矩陣。一個數值優化問題,這里就不詳細講了。4) 迭代我們優化得到了一個新的R與T,導致了一些點轉換后的位置發生變化,一些最鄰近點對也相應的發生了變化。 因此,我們又回到了步驟2)中的尋找最鄰近點方法。2)3)步驟不停迭代進行,直到滿足一些迭代終止條件,如R、T的變化量小于一定值,或者上述目標函數的變化小于一定值,或者鄰近點對不再變化等。(這里也是題主所說的ICP算法中的一個參數) 算法大致流程就是上面這樣。這里的優化過程是一個貪心的策略。首先固定R跟T利用最鄰近算法找到最優的點對,然后固定最優的點對來優化R和T,依次反復迭代進行。 這兩個步驟都使得目標函數值下降,所以ICP算法總是收斂的,這也就是原文中收斂性的證明過程。這種優化思想與K均值聚類的優化思想非常相似,固定類中心優化每個點的類別,固定每個點的類別優化類中心。 關于參數的選擇: ICP算法的參數主要有兩個。一個是ICP的鄰近距離,另外一個是迭代的終止條件。這些參數的選擇,與實際的工程應用相關。比如說你的儀器精度是5mm,那么小于5mm是可以認為是對應點,而最終的迭代終止條件也就是匹配點之間平均距離小于5mm。 而且這些參數可以由算法逐步迭代減小,最初使用較大的對應點距離參數,然后逐步減小到一個較小的值。(問過師兄才知道實際過程這樣操作會比較合適。)需要手動調整一些參數。(這跟機器學習調參比起來,簡直不是事~)
3
粗配準前面介紹到了,ICP算法的基本原理。它需要一個旋轉平移矩陣的初值。這個初值如果不太正確,那么由于它的greedy優化的策略,會使其目標函數下降到某一個局部最優點(當然也是一個錯誤的旋轉平移矩陣)。因此,我們需要找到一個比較準確的初值,這也就是粗配準需要做的。 粗配準目前來說還是一個難點。針對于不同的數據,有許多不同的方法被提出。 我們先介紹配準的評價標準,再在這個標準下提出一些搜索策略。 評價標準:比較通用的一個是LCP(Largetst Common Pointset)。給定兩個點集P,Q,找到一個變換T(P),使得變換后的P與Q的重疊度最大。在變換后的P內任意一點,如果在容差范圍內有另外一個Q的點,則認為該點是重合點。重合點占所有點數量的比例就是重疊度。 解決上述LCP問題,最簡單粗暴的方法就是遍歷。假設點集P,Q的大小分別為m,n。而找到一個剛體變換需要3對對應點。 那么brute force 搜索的需要的復雜度。對于動輒幾百萬個點的點云,這種時間復雜度是不可接受的。 因此,許多搜索策略被提出。比較容易想到的是RANSAC之類的搜索方法。而對于不同的場景特點,可以利用需配準點云的特定信息加快搜索。(例如知道點云是由特定形狀的面構成的)這里先介紹一個適用于各種點云,不需要先驗信息的搜索策略,稱為4PC(4 Point Congruent)。 搜索策略:4PC搜索策略是在P,Q中找到四個共面的對應點。
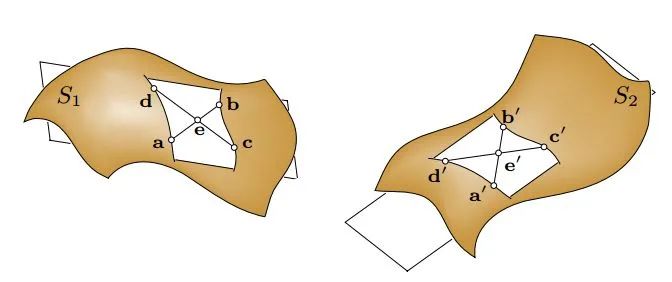
如上圖所示(來自4PC原文),這四個共面的點相交于e。這里有兩個比例在剛體變化下是不變的。(實際上在仿射變換下也是不變的) 
 而4PC將對于三個點的搜索轉換為對e,e'的搜索,從而將復雜度降低到了
而4PC將對于三個點的搜索轉換為對e,e'的搜索,從而將復雜度降低到了 。 這四個點的距離越遠,計算得到的轉換越穩健。但是這里的四個點的搜索依賴于兩個點云的重疊度。 具體的算法可以參考4-Points Congruent Sets for Robust Pairwise Surface Registration的原文。 4PC算法通用性較好,但是對于重疊度較小、或是噪聲較大的數據也會出現配準錯誤或是運行時間過長的問題。針對于不同的場景很多其他的搜索策略也被提出。 這里安利一下我師兄的論文吧~Automatic registration of large-scale urban scene point clouds based on semantic feature points 我們課題組主要是研究室外地面站LiDAR獲取的點云配準問題。這種情形下,由于掃描儀內有自動安平裝置,Z軸都是豎直方向(重力方向),剛體變換只存在三維平移與平面(XoY面上的)旋轉。我們就在場景中搜索豎直的特征線并且得到它們與地面的交點。
。 這四個點的距離越遠,計算得到的轉換越穩健。但是這里的四個點的搜索依賴于兩個點云的重疊度。 具體的算法可以參考4-Points Congruent Sets for Robust Pairwise Surface Registration的原文。 4PC算法通用性較好,但是對于重疊度較小、或是噪聲較大的數據也會出現配準錯誤或是運行時間過長的問題。針對于不同的場景很多其他的搜索策略也被提出。 這里安利一下我師兄的論文吧~Automatic registration of large-scale urban scene point clouds based on semantic feature points 我們課題組主要是研究室外地面站LiDAR獲取的點云配準問題。這種情形下,由于掃描儀內有自動安平裝置,Z軸都是豎直方向(重力方向),剛體變換只存在三維平移與平面(XoY面上的)旋轉。我們就在場景中搜索豎直的特征線并且得到它們與地面的交點。
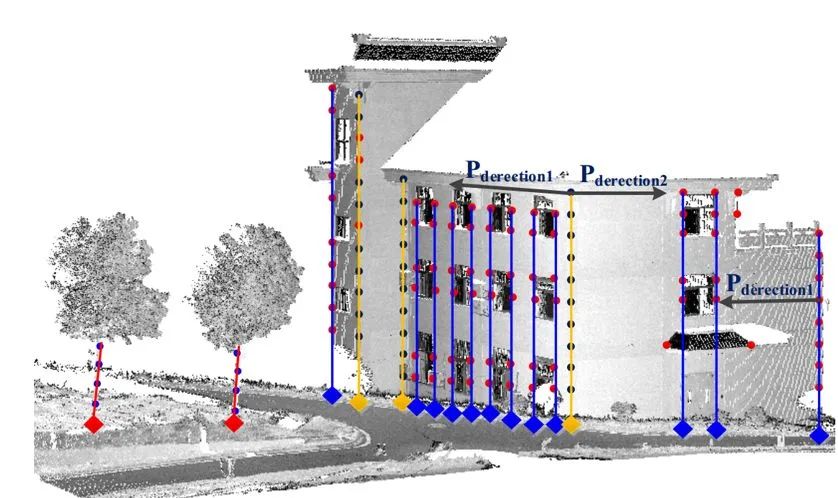
再將這些交點構建出三角形,以三角形的全等關系來得到匹配。
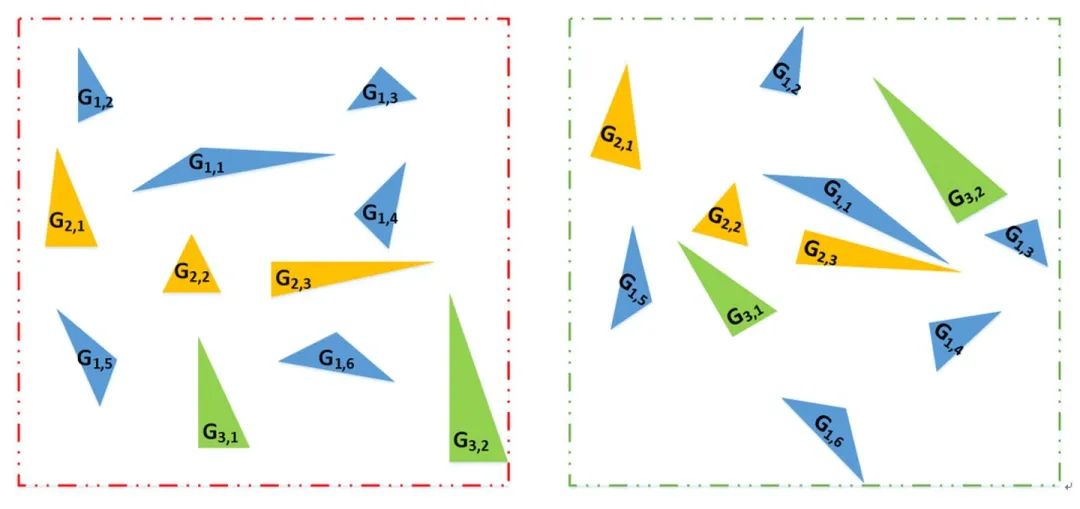
找出其中一致性最好的三角形集合,作為匹配的集合,進行粗配準。 這種方法適用于豎直線較多的場景,比如城區的建筑物的邊線、林區樹木的樹干等。設計的方法還是很巧妙的。當然如果場景內這種特征較少,就比較難以配準。
參考文獻
[1] Besl P J, Mckay N D. Method for registration of 3-D shapes[C]// Robotics - DL tentative. International Society for Optics and Photonics, 1992:239-256. [2] Aiger D, Mitra N J, Cohen-Or D. 4-points congruent sets for robust pairwise surface registration[J]. Acm Transactions on Graphics, 2008, 27(3):85. [3] Yang B, Dong Z, Liang F, et al. Automatic registration of large-scale urban scene point clouds based on semantic feature points[J]. Isprs Journal of Photogrammetry & Remote Sensing, 2016, 113:43-58.
-
ICP
+關注
關注
0文章
70瀏覽量
12802 -
點云配準
+關注
關注
0文章
4瀏覽量
806 -
點云
+關注
關注
0文章
58瀏覽量
3806
原文標題:三維點云配準的相關知識學習技巧(粗配準&精配準)
文章出處:【微信號:vision263com,微信公眾號:新機器視覺】歡迎添加關注!文章轉載請注明出處。
發布評論請先 登錄
相關推薦
三維測量軟件的使用技巧
三維掃描與建模的區別 三維掃描在工業中的應用
基于深度學習的三維點云分類方法
什么是三維點云分割
友思特方案 基于三維點云實現PCB裝配螺絲視覺檢測

泰來三維|三維掃描文物拍照模型制作
友思特案例 | 自研創新!三維工件尺寸測量及點云處理解決方案
泰來三維|三維掃描服務_三維激光掃描儀測量山體滑坡點云建模
泰來三維|三維掃描點云數據怎么處理如何建模
泰來三維|文物三維掃描,文物三維模型怎樣制作





 三維點云配準的相關知識學習技巧
三維點云配準的相關知識學習技巧













評論