在信號采集系統中,除了我們感興趣的數據外,難免會有一些來自于環境的干擾信號。但我們總希望我們得到的數據是純凈而真實的,為了達到這個目標,我們不得不想辦法去除這些干擾信號,于是濾波器就成為我們必不可少的幫手。這一篇我們就來討論如何通過軟件實現基于中值平均算術平均算法的中值數字濾波器。
1、問題的提出
??在我們通過AD采集獲取數據時,不可避免會受到干擾信號的影響,而且很多時候我們希望盡可能的將這種影響減到最小。為實現這一目的,人們想了很多辦法,有硬件方面的,也有軟件方面的。在硬件難以改變或者軟件能夠達到相應效果時,我們一般采用軟件方法來實現,通常稱之為數字濾波。
??在我們的項目中,要求100毫秒采集100個數據,由于信號非常微弱,很容易收到干擾,所以實際采集到的數據中起伏很大,這其中有很多數據數疊加了干擾項的數據。通過示波器觀察,我們發現在這些干擾項中,有周期性的頻率相對低一些的干擾,也有無規律的頻率很高的干擾。這些干擾信號對我們的測量結果的影響非常之大,幾乎讓測量結果完全不可信,所以我們必須想辦法將其去除。
??我們考慮并測試了多種濾波算法,我們發現單一的濾波手段很難同時濾掉幾種不同的干擾信號。所以我們嘗試組合多種濾波算法以實現我們的目標。
2、算法設計
??前面我們已經描述了問題的來源,所以為了去除不同種類的干擾信號,我們必須設計一個針對多種干擾信號的濾波算法。我們知道主要的干擾信號是相對頻率較低的周期干擾和相對頻率較高的非周期干擾,我們將分析這兩種信號的特點并針對性的采取相應的濾波手段。
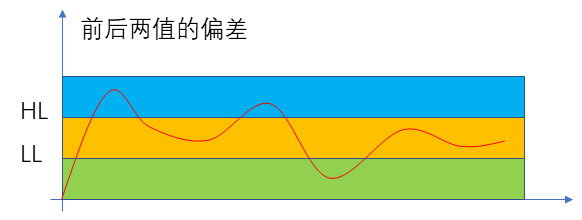
??首先我們來考慮相對頻率較低的周期干擾,這種干擾來自于環境并且很難避免,但這種干擾信號具有一定的規律,所以它對正常信號造成的影響也是有一定規律的。我們可以圖示如下:
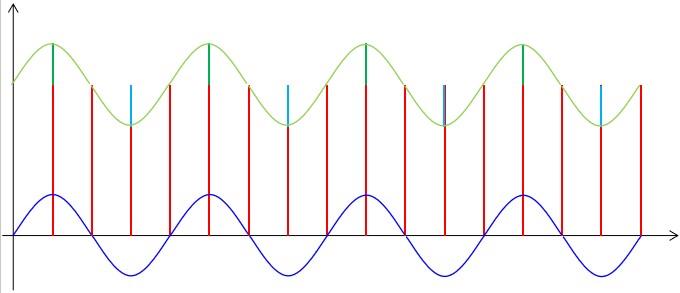
??如果只存在這一種周期性的低頻率的干擾信號,那么我們很容易想到采用算術平局算法就能夠去除,在前面我們也確實是這么做的。事實上如果存在多種頻率的周期性干擾信號,只要采集到的數據樣本數量足夠,采用算數平均算法基本都是可以得到比較理想的結果。在我們的項目中,我們的采集頻率達到了1KHz,而我們每100毫秒出一個數,所以從理論上講,10Hz以上的周期性干擾都可以通過算術平均率波來消除。
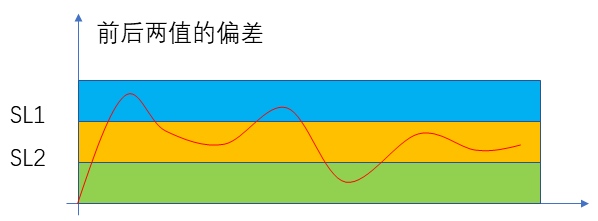
??接下來我們來考慮相對頻率較高的非周期干擾,這種干擾具有較大的隨機性,有可能對信號的影響較大,也有可能對信號的影響較小,其頻率和幅值都是隨機的,測量結果存在很大的偶然性。我們可以簡單的圖示如下:
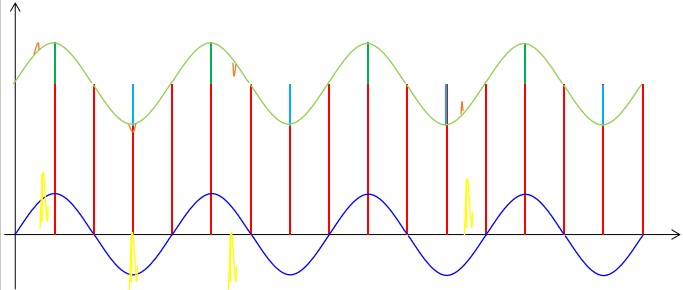
??對于這種干擾我們前面的方法對他是沒有效果的,但我們的ADC采用的是積分方式來檢測信號的,所以在兩個采樣點之間,無論這類干擾信號在何時出現都會疊加到緊接著的這個采樣數據上,致使最終的采樣數據比周期性干擾疊加的情況下要么大一些,要么小一些。這就存在兩種情況,如果是正向干擾就會是數據變大一些,如果是反向干擾就會是數據變小一些。使得最終的測量數據更加背離原始數據或者更加接近原始數據。
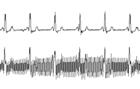
??對于更加接近我們需要的數據的變化,我們先不用理會它,畢竟它更加接近我們想要的數據。對于更加偏離的那一部分數據,我們有什么辦法將其去除掉呢?辦法是有的,我們借鑒比賽積分中去掉偶然性的方式,去掉最高和最低的數,中間的數應該更接近與真實值。具體如下圖所示:
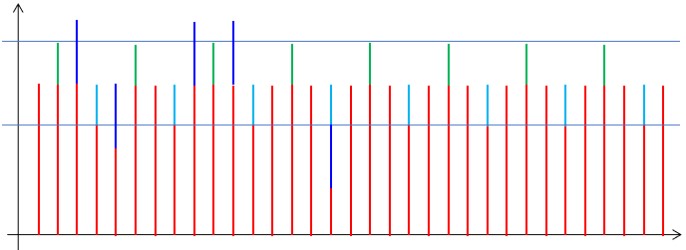
??這樣去掉最大的一些數和最小的一些數后,并不能保證得到的就是真實的信號值,但有一點我們時刻以肯定的就是,余下的值都更為接近真實的信號值。然后我們在對余下的數采取算術平均操作,得到的就是接近真實值的一個采集值了。
3、編碼實現
??我們已經設計了采用中值及算術平均的方式的算法來處理這些數據。但具體該如何實現呢?這一節中我們就來討論算法的實現。
??首先我們來分析一下實現這里算法需要涉及到哪些問題。第一,首先我們必須采集到一定數量的數據,這個數據量不可太小,理論上來講3個數據可以實現,但事實上你會發現對此等規模的數據量使用這一算法其實沒有多大意義。一般一次采集幾十個數然后再做此濾波是比較有效果的。第二,因為采用丟棄一定數量的極大值和極小值減少干擾項的方法,所以在幾十上百的數據量時,我們最好是將其先排序在去除比較方便。第三,我們需要選擇合理的基礎數據量和需要去除的極大極小數量。這一點對最終的結果和濾波的效果都會有影響。明白了上述幾點后,我們就可以來實現這一濾波算法了。
/*中值平均濾波算法*/
static uint32_t MedianMeanFilter(uint32_t *pData,uint16_t aSize,uint16_t eSize)
{
uint32_t tData;
uint32_t result=0;
if(aSize<=2*eSize)
{
return 0;
}
for (int i=0; i-1; i++) //比較n-1輪
{
for (int j=0; j-1-i; j++) //每輪比較n-1-i次,
{
if (pData[j] < pData[j+1])
{
tData = pData[j];
pData[j] = pData[j+1];
pData[j+1] = tData;
}
}
}
for(int j=eSize;j<(aSize-eSize);j++)
{
result=result+pData[j];
}
result = result/(aSize-2*eSize);
return result;
}
??在上述實現中,我們先對輸入的數據進行了排序。在上述代碼中我們考慮到數據量不大,采用了冒泡排序的方式實現。然后我們去除了一定數量的極大值和極小值,并對余下的值取算術平均就得到了本次我們的采集值。
??對于函數中的三個參數:uint32_t *pData是需要濾波的原始采集數據;uint16_t aSize是需要濾波的原始采集數據的數量;uint16_t eSize是需要丟棄的極大值和極小值的數量。其中aSize要遠大于eSize的2倍,否則大部分被舍棄,濾波的意義就不大了。
??函數的使用也很簡單。比如在我們的應用中,我們以1KHz的速度采集原始值,每采集100個數出一個測量結果,去掉10個極大值和10個極小值,于是我們就可以調用函數如下:
temp[i]=MedianMeanFilter(rDatas[i],100,10);
??在這個應用中,我們測試去掉10個極大值和10個極小值可以得到比較理想的結果,當然也可以將eSize的值增大一些以強化濾波的效果,但不要太大。
4、應用總結
??我們實現了基于算術平均的中值濾波器。該濾波器對一定頻率以上的周期性干擾和隨機性的噪聲干擾均有較好的效果。通過修改丟棄的極大值和極小值的數量可以應對在不同環境下的濾波要求。
??這一濾波算法適用于高速采集,大數據量的情況下濾波。所以必須采集到一定數量的數據,這個數據量不可太小。一般一次采集幾十個數然后再做此濾波是比較有效果的。
??這一濾波算法對一定頻率以上的周期性干擾和隨機性的高頻干擾有顯著的效果。而對其他類型的干擾只具有有限的改善。
-
濾波器
+關注
關注
161文章
7817瀏覽量
178139 -
數字濾波器
+關注
關注
4文章
270瀏覽量
47026 -
算法設計
+關注
關注
0文章
24瀏覽量
8150
發布評論請先 登錄
相關推薦
使用FPGA構建的數字濾波器設計方案

基于算術平均算法的限幅濾波器設計




 基于算術平均算法的中值數字濾波器設計
基于算術平均算法的中值數字濾波器設計
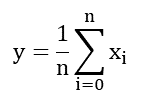












評論