分辨率優于16位的高精度快速模數轉換器(ADC)的交流性能測試和驗證需要能夠覆蓋至少0 kHz至20 kHz音頻帶寬的近乎完美的正弦波發生器。通常,使用昂貴的實驗室儀器來執行這些評估和表征,例如Audio Precision的音頻分析儀AP27xx或APx5xx系列。大多數情況下,具有24位或更高尺寸的現代高速SAR和寬帶Σ-Δ型ADC具有單電源和全差分輸入,因此要求用于DUT的信號源具有直流和交流精度,同時提供全差分輸出(180°異相)。同樣,該交流發生器的噪聲和失真電平應遠優于這些ADC的規格,因此本底噪聲電平遠低于–140 dBc,失真低于–120 dBc,輸入音調頻率為1 kHz或2 kHz,根據大多數供應商規格,最高可達20 kHz。適用于高分辨率寬帶ADC的典型臺架測試設置的典型配置如圖1所示。最關鍵的組件是正弦波發生器(單音或多音),在這里,基于軟件的直接數字頻率合成器(DDS)可以提供充分的靈活性,具有極精細的頻率分辨率和時鐘與數據采集系統的時鐘同步,以執行相干采樣以避免泄漏和FFT窗口濾波。
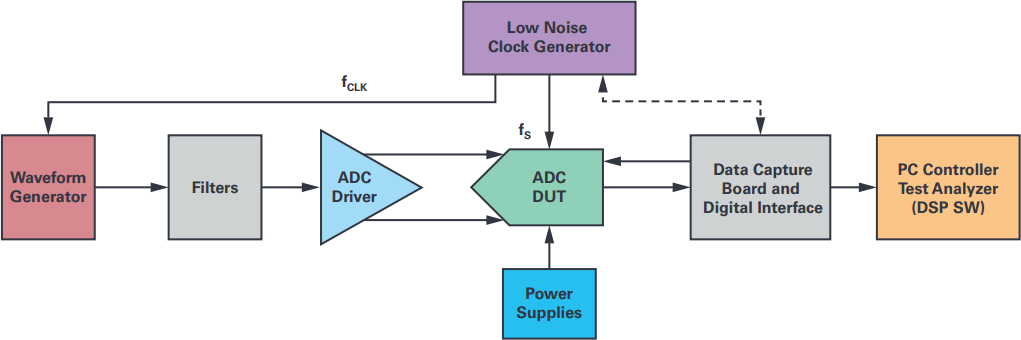
圖1.基于 IEEE 1241 標準的典型 ADC (ac) 測試設置的處理鏈。DDFS 使整個測量系統完全數字化,具有許多優點,包括完全的靈活性和相干采樣采集。
只需音頻精密分析儀的一小部分成本,就可以設計出基于直接數字頻率合成(DDFS)原理的非常精確的正弦波發生器,但在浮點DSP處理器(如SHARC處理器)上通過軟件實現。相當快的浮點DSP將滿足實時期望,并滿足所有算法和處理條件,以實現最先進的SAR ADC設置的失真和噪聲性能水平。利用用于NCO相位累加的32位或64位定點格式的SHARC內核架構的全字數據長度,以及執行正弦近似函數和用于整形頻譜的數字濾波器的專有40位浮點擴展精度,與用于 信號重建。
直接數字頻率合成
數字信號發生器合成器專利于1970年4月由Joseph A. Webb提交1描述了什么可以被認為是DDS機制的基礎,只需使用幾個數字邏輯模塊即可生成各種類型的模擬波形,包括正弦波。然后,在1971年初,經常被引用的參考論文來自Tierney等人。2通過深化正交生成的DDS運算及其對采樣系統理論的局限性(字截斷和頻率規劃)發表了直接數字頻率生成。實際實現開始出現,主要依賴于分立標準邏輯IC,如TTL 74xx或ECL 10K系列。不到10年后,斯坦福電信、高通、普萊西和ADI等公司推出了AD9950和AD9955等完全集成的解決方案。邏輯IC的架構基于查找表(LUT),旨在實現最佳速度、功耗和成本權衡,以確保在有限的相位、頻率和幅度分辨率下進行相位到正弦幅度的轉換。如今,ADI公司仍然是DDS獨立集成電路的最大、或許也是最獨特的供應商,而當前的數控振蕩器(NCO)往往集成在AD9164或AD9174等RF DAC中。盡管這些器件在多GHz帶寬下具有令人印象深刻的噪聲和線性度性能,但它們都不適合測試LTC2378-20、AD4020或AD7768等中等速度、高分辨率ADC。
與傳統的基于 PLL 的頻率合成器相比,NCO 和 DDS 以其非常精細的頻率分辨率、快速的敏捷性以及具有完美正交的正弦/余弦生成容易而聞名。它們還因其寬帶寬覆蓋范圍和直流精度而備受推崇。其工作原理受數字信號處理和采樣系統理論的支配,其數字性質允許對輸出信號的相位、頻率和幅度進行完全數字化和獨立的控制。圖2的框圖描述了傳統DDS的架構,它由三個主要功能組成:
N位相位累加器;
一種相位-正弦振幅轉換器,其特征在于W位截斷的相位輸入字;
D位DAC及其相關的重建濾波器。
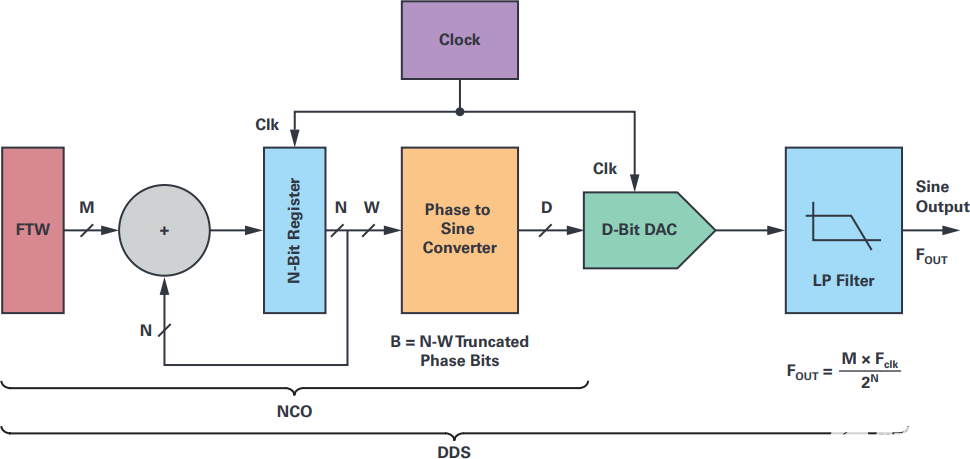
圖2.NCO的主要功能部分與完整的直接數字合成器區別開來,其中包括重建DAC及其相關的AAF。NCO 部分可用于測試或激勵 DAC。
相位累加器圍繞一個簡單的N位加法器構建,該加法器與寄存器相結合,寄存器的內容以采樣時鐘F的速率更新時鐘輸入相位增量 Δθ,通常也稱為頻率調諧字 (FTW)。累加器可以周期性地溢出,并像采樣時鐘或參考時鐘F之間的小數分頻器一樣工作時鐘和 DDS 輸出頻率 F外,或者像變速箱一樣,分頻比等于:
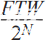
溢出速率給出了生成波形的輸出頻率,使得:
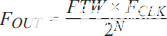
其中 0 ≤ FTW ≤ 2N–1.由于分頻器效應,參考或采樣的貢獻fSNCO輸出端的時鐘相位噪聲將降低
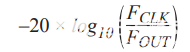
相位累加器寄存器的輸出表示所生成波形的當前相位。然后,借助相位到正弦或相到余弦映射器引擎,每個離散累加器輸出相位值被轉換為幅度正弦或余弦數據或樣本。此功能通常通過存儲在LUT(ROM)中的三角函數值來實現,有時通過執行正弦近似算法或兩者的組合來實現。相位-正弦幅度轉換器的輸出饋入DAC,DAC在濾波之前產生量化和采樣正弦波,以平滑信號并避免頻譜混疊。DAC有限分辨率施加的幅度量化對本底噪聲和合成器的信噪比(SNR)施加了理論限制。此外,作為混合信號器件,DAC由于其INL、DNL、壓擺率、毛刺和建立時間特性而表現出一大堆直流和交流非線性,這些特性會產生雜散音并降低正弦波發生器的整體動態范圍。
基于圖2架構的實際正弦波形發生器實現主要區別在于相位幅度轉換器模塊,由于數字無線電應用的市場導向,該模塊通常針對速度和功耗進行優化,而不是高精度。實現相位-正弦幅度轉換器的最簡單方法是使用ROM通過一對一映射存儲正弦值。不幸的是,LUT 的長度呈指數級增長(2N),相位累加器的寬度為N,波表數據字精度為線性。 不幸的是,減小累加器尺寸或截斷其輸出的權衡會導致頻率分辨率的損失和SFDR的嚴重退化。結果表明,由相位或幅度量化引起的雜散遵循–6 dB/位的關系。由于通常需要大N來實現精細的頻率調諧,因此已經推廣了幾種技術來限制ROM尺寸,同時保持足夠的雜散性能。通常使用簡單的壓縮方法,利用正弦或余弦函數的四分之一波對稱性將相位參數范圍減小4。為了進一步縮小范圍,相位累加器輸出的殘酷截斷是事實上的方法,盡管它確實引入了雜散諧波。盡管如此,由于精細的頻率分辨率要求、內存大小和成本妥協,始終采用這種方法。已經提出了各種角度分解方法,以降低基于LUT的方法的內存需求。結合使用各種類型的分割、線性或多項式插值的幅度壓縮,其想法是精確地近似正弦函數的第一象限,或者在需要正弦和余弦函數的 I/Q 合成的情況下,精確地接近 [0, π/4] 區間。同樣,基于角度旋轉的算法有效地支持了沒有ROM LUT的復雜信號生成,只需在逐次逼近方案中進行移位和加法操作。這種方法以流行的CORDIC為代表,當硬件乘法器不可用或出于速度或成本考慮應最小化實現功能所需的門數(在FPGA或ASIC中)時,通常比其他方法更快。相反,當硬件乘法器可用時(DSP微處理器中總是如此),使用插值方法和完整的多項式計算(例如泰勒級數展開)進行表查找時,切比雪夫多項式比CORDIC更快,尤其是在必須高精度的情況下。
在軟件中實現高精度 NCO。
構建具有與最佳模擬振蕩器相似或更好的失真性能的高精度交流音發生器,如最著名的惠普分析儀或應用筆記 AN-132 中所述3即使專用于音頻頻譜(直流至20 kHz范圍),也不是一件小事。然而,如前所述,完整的軟件實現,使用嵌入式處理器的足夠算術精度執行相位計算(ωt)和正弦函數(sin(ωt))近似,當然可以幫助最大限度地減少量化副作用,噪聲和由此產生的雜散。這意味著圖2中的所有NCO功能塊都轉換為代碼行(無VHDL!),以實現滿足實時約束的軟件版本,以確保最小采樣率和所需的頻率帶寬。
對于相位到正弦幅度轉換引擎,完整的LUT方案或任何變化都需要太多的內存或太多的插值操作才能實現完美的正弦一致性。相反,正弦近似的多項式方法允許使用成本非常低的通用DSP,從而提供了非常好的復雜度與精度權衡。多項式級數擴展也非常有吸引力,因為它相對簡單,并且能夠在選擇冪級數類型時提供充分的靈活性,為給定精度定制算法。它不需要大的內存空間,少于100行SHARC DSP裝配線,只需要幾個RAM位置來存儲多項式系數和變量,因為正弦值僅在采樣時計算。
首先,正弦近似函數的明顯選擇是使用具有適當順序的直泰勒/麥克勞林冪級數來滿足目標精度。但是,由于冪級數往往會在端點上失去有效性,因此在執行任何多項式計算之前,必須將參數輸入范圍減小到較小的間隔。如果不減少參數范圍,函數域(如 [–π, +π] )上的高精度只能通過非常高階多項式來支持。因此,需要將一些變換應用于初等函數以獲得簡化的參數,例如 sin(|x|) = sin(f + k × π/2) 和 sin(f) = sin(x – k × π/2) 為 0 ≤f<π/2。因此,三角函數應格外小心,以避免減法抵消,這將導致精度嚴重損失并產生災難性結果,尤其是在算術精度較差的情況下。在我們的例子中,當相位輸入很大或接近π/2的整數倍時,可能會發生這種情況。
除了周期性和模-2π重復之外,sin(x)函數的對稱性質還可以用于進一步縮小近似范圍。鑒于正弦函數在區間 [0, 2π] 的點 x = π 上是反對稱的,因此可以使用以下關系:
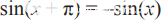
將范圍減小到 [0, π]。以同樣的方式,sin(x) 顯示了區間 [0, π] 由 x = π/2 定義的直線的對稱性,使得:
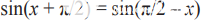
對于區間 [0, π/2] 中的 x,這進一步減小了角度輸入近似范圍。進一步將參數簡化為較小的區間(如 [0, π/4] 以提高精度是沒有效率的,因為它需要同時計算正弦和余弦函數,這是由共同三角關系決定的:sin(a+b) = sin(a) × cos(b) + cos(a) × sin(b),這對于生成正交音來說是值得的。
ADI公司的ADSP-21000系列應用手冊第1卷介紹了一種幾乎理想的(用于嵌入式系統)正弦逼近函數,該函數基于為首款ADI DSP浮點處理器(即ADSP-21020)編寫的優化功率級數,該處理器基本上是一個SHARC內核。sin(x) 的這種實現依賴于 Hart 等人發表的最小最大多項式近似。4并由科迪和韋特改進5用于浮點運算,以減輕舍入誤差并避免發生前面提到的取消。最小最大值方法依賴于切比雪夫多項式和雷梅茲交換算法來確定所需最大相對誤差的系數。如圖 3 中的 MATLAB 所示,與七階泰勒多項式的泰勒相比,設置系數的微小變化會導致極小最大值的精度顯著提高。?6為了獲得最佳精度與速度權衡,此正弦近似函數的角度輸入范圍縮小到[–π/2至+π/2]間隔,并且軟件例程包括一個高效的范圍縮小濾波器,約占總“正弦”子程序執行時間的30%。
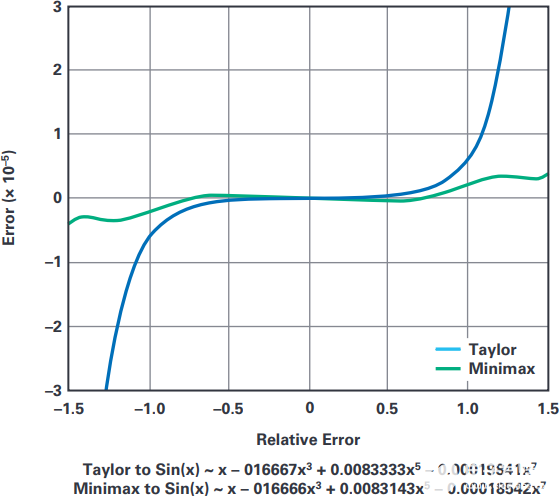
圖3.與在 0 左右定義的 Taylor-MacLaurin 方法不同,最小最大值正弦近似方法最小化并均衡了 [–π/2 至 +π/2] 區間內的最大相對誤差。
雖然所有的計算都可以用32位定點算法執行,但數學計算最常見和最方便的格式,特別是在處理長數時,多年來一直是IEEE 754浮點標準。作為DSP VLSI芯片制造商,ADI公司從一開始就率先推出了IEEE 754-1985標準。當時,根本沒有單芯片浮點DSP處理器,只有簡單的浮點乘法器和ALU計算IC,例如ADSP-3212和ADSP-3222。這種格式取代了計算機行業的大多數專有格式,并成為所有SHARC DSP處理器的原生格式,包括單精度32位、擴展精度40位,以及最近ADSP-SC589和ADSP-SC573的雙精度64位。
SHARC 40 位擴展單精度浮點格式及其 32 位尾數提供足夠的精度 (u 2–32) 對于這個正弦波生成應用程序并保持相等,Cody 和 Waite 表明 15千階多項式適用于 32 位的總體精度,在 [0 到 +π/2] 輸入域上均勻分布誤差。最小化操作次數并保持準確性的最后一個調整是實現多項式計算的霍納規則,這是一種快速冪法,用于評估一個點的多項式,例如:
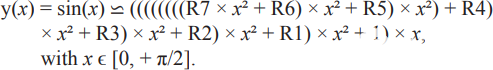
R1 到 R7 是多項式級數的 Cody 和 Waite 系數,只需要 8 次乘法和 7 次加法即可計算任何輸入參數 ε[0, π/2] 的正弦函數。以匯編子例程形式編寫的完整 sin(x) 近似代碼在 SHARC 處理器上以大約 22 個內核周期執行。原始程序集子例程經過修改,以便在獲取 40 位多項式浮點系數時同時執行雙內存訪問,以節省六個周期。
NCO 64 位相位累加器本身正在利用雙精度 2 補碼分數格式的 SHARC 32 位 ALU 來執行。一個完整的相位累加器執行和內存更新需要 11 個內核周期,因此,每個 NCO 輸出樣本在大約 33 個內核周期內生成。
圖4中的圖表顯示了基于DSP的軟件NCO的功能塊實現,并參考了每個階段的算術格式精度。此外,信號模擬重建需要一個或兩個DAC及其模擬抗混疊濾波器電路,并實現完整的DDFS。處理鏈的關鍵要素是:
64位相位累加器(帶溢流的SHARC ALU雙精度加法);
64位小數定點到40位FP轉換模塊;
范圍縮小塊 [0 到 + π/2] 和象限選擇(科迪和韋特);
用于相位到幅度轉換的正弦近似算法(Hart);
–1.0 至 +1.0 范圍內的 sin(x) 重建和歸一化階段;
LP FIR 濾波器和 sin(x)/x 補償(如有必要);
以及 40 位 FP 到 D 位定點轉換和縮放功能,以適應 DAC 數字輸入。
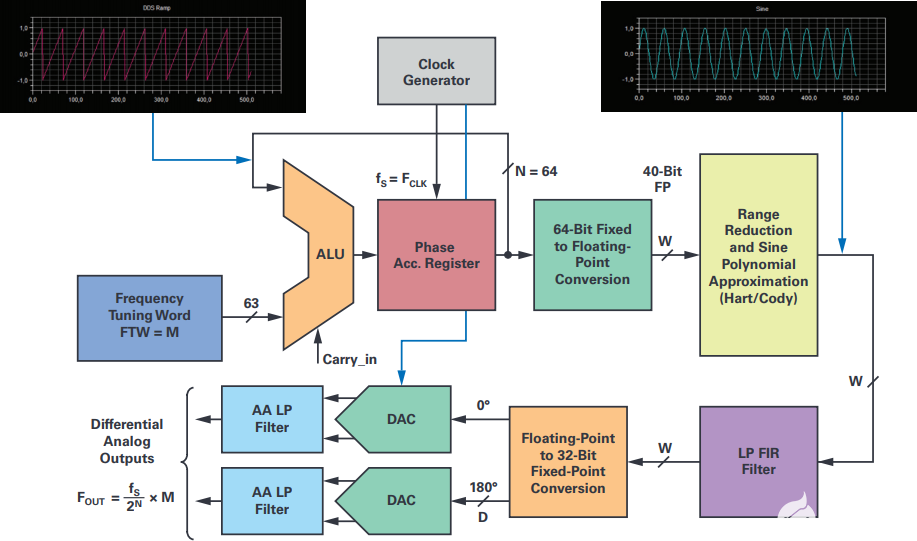
圖4.DDS軟件簡化框圖給出了數據算術格式和處理元件之間各種量化步驟的位置。
可以在NCO的輸出端放置一個可選的數字低通濾波器,以消除可能在目標頻帶中折疊的任何雜散和噪聲。或者,該濾波器可以提供插值和/或反sin(x)/x頻率響應補償,具體取決于為模擬重建選擇的DAC。這種低通FIR濾波器可以使用MATLAB濾波器設計器工具進行設計。例如,假設采樣頻率為48 kSPS,直流至20 kHz帶寬,帶內紋波為0.0001 dB,帶外衰減為–150 dB,則可以使用40位浮點系數實現高質量的等紋波濾波器。由于只有 99 個濾波器系數,其總執行時間將在單指令、單數據 (SISD) 單計算單元模式下消耗約 120 個 SHARC 內核周期。數字濾波后,DMA使用其中一個DSP同步串行端口將計算出的樣本對發送到DAC。為了獲得更好的速度性能,還可以使用大型乒乓內存緩沖區鏈接 DMA 操作,以支持按塊操作進行處理。例如,塊數據大小可以等于 FIR 數據延遲線的長度。
NCO 的最終調整以實現最佳 SFDR
如前所述,NCO受到雜散的影響主要是由于相位累加器輸出的截斷,以及在較小程度上,由于通過計算或制表獲得的正弦值進行的幅度量化。相位截斷引起的誤差通過相位調制(鋸齒波)在載波頻率附近產生雜散,而正弦幅度量化會導致諧波相關的雜散,盡管長期以來被認為是隨機誤差和噪聲。今天,相位累加器的操作在數學上是完美的,如技術論文中所述。7來自亨利·T·尼古拉斯和H·薩繆利。經過徹底分析后,提出了一個模型,使得相位累加器被認為是離散相位采樣置換發生器,從中可以預測頻率雜散。無論相位累加器參數(M、N、W)如何,相序的長度都等于
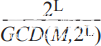
(其中GCD是最大公約數)由頻率調諧字M的最右邊位位置L決定,如圖4所示。因此,L 的值定義了序列類,每個序列類共享自己的一組相位分量,但根據
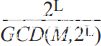
率。這些在時域中生成的截斷相位樣本序列用于通過DFT確定頻域中每條雜散線的相應位置和幅度。這些序列還表明,M(FTW)的奇數值表現出最低頻率雜散的幅度,并建議對相位累加器進行簡單的修改,只需在FTW中添加1 LSB即可滿足這些最小條件。這樣,相位累加器輸出序列被強制始終具有相同的 2N相位元素,無論相位累加器的M值和初始內容如何。然后,最差雜散音幅度的電平降低3.922 dB,等于SFDR_min(dBc)= 6.02 × W。Nicholas改進的相位累加器為NCO帶來了幾個好處,因為首先它消除了FTW最右邊太接近其MSB(FMCW應用中的頻率掃描)的情況,其次,它使雜散的幅度與頻率調諧字M無關。通過在采樣率f下切換ALU LSB,可以在軟件中輕松實現此修改S,可以模擬相位累加器的相同行為,就像將FTW LSB設置為邏輯1一樣。當相位累加器大小N = 64位時,1/2 LSB偏移可以被認為是關于所需頻率F精度的可忽略不計的誤差外.
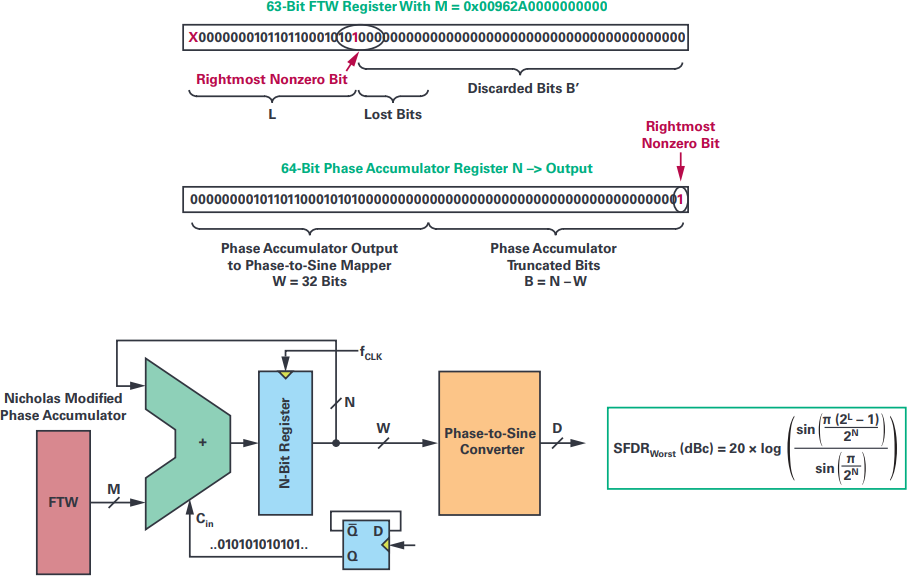
圖5.FTW 最右邊的非零位的位置設置了理論上的 SFDR 最壞情況水平。尼古拉斯修改的相位累加器解決了N的任何值的問題,并使NCO的SFDR最大化。
輸出相位字W為32位時,相位截斷導致的最大雜散幅度被限制在–192 dBc!正弦采樣值的有限量化也會導致另一組頻率雜散,它通常被認為是噪聲,并通過眾所周知的關系SNR進行估計q(分貝) = 6.02 × D + 1.76。由于相位-正弦幅度轉換算法級的近似誤差,必須將其添加到寄生元件中,但是,考慮到在選擇相位-正弦近似算法和計算精度時非常謹慎,該誤差被認為是可以忽略不計的。
這些結果表明,我們的軟件正弦NCO的線性度和噪聲都處于理論水平,遠遠超出了測試市場上大多數高精度ADC所需的閾值。信號鏈中最后一個但最關鍵的元件還有待找到:重建DAC及其互補模擬抗混疊濾波器以及相關的驅動器電路,這些電路很容易滿足預期的性能水平。
重建DAC:事情的致命弱點!
第一個誘惑是選擇在非線性誤差(INL和DNL)方面具有最佳規格的高精度DAC,例如出色的AD5791,這是一款20位精度的DAC。但它的分辨率只有20位,其R-2R架構不利于信號的重建,尤其是非常純正弦曲線的產生,因為它在輸入代碼轉換期間有很大的毛刺。圍繞二進制加權電流發生器或電阻網絡構建的傳統DAC架構對數字饋通和數字開關損傷(如外部或內部時序偏斜以及數字輸入位的其他開關不對稱)很敏感,特別是在導致能量變化的主要轉換期間。這會引起與代碼相關的瞬變,從而產生高振幅的諧波雜散。
在20+位分辨率下,使用外部超線性快速采樣保持放大器來消除DAC輸出的毛刺沒有多大幫助,因為它會在數十個LSB中產生自己的瞬變,并且由于重新采樣而引入群延遲非線性。對于信號重建,主要是在通信應用中,通過使用分段架構來解決毛刺問題,該架構將完全解碼的部分混合用于MSB,二進制加權元素用于最低有效位。遺憾的是,目前沒有超過16位精度的商用DAC。與NCO完全可預測的行為不同,DAC誤差很難準確估計和仿真,特別是當制造商的動態規格相當弱或不存在時,除了專用于音頻應用的DAC或ADC。因此,插值過采樣和多位Σ-Δ DAC似乎是唯一足以勝任這項工作的解決方案。這些先進的轉換器具有高達 32 位的分辨率、超低失真和高 SNR,是中低帶寬信號重建的最佳候選者。為了在音頻頻譜或稍寬的頻段(20 kHz或40 kHz帶寬)內獲得最佳噪聲和失真性能,ADI公司產品組合中最好的Σ-Δ型DAC是AD1955音頻立體聲DAC,盡管其分辨率限制為24位,但它仍然是市場上最好的音頻DAC之一。
這款音頻DAC于2004年推出,基于多位Σ-Δ調制器和過采樣技術,并輔以各種技巧,以減輕失真和這種轉換原理固有的其他困擾。8
即使在今天,AD1955也擁有同類產品中最好的插值LP FIR濾波器之一。它具有非常高的阻帶衰減 (≈–120 dB) 和非常低的帶內紋波 (≈±0.0001 dB)。其兩個(左聲道和右聲道)DAC的工作頻率最高可達200 kSPS,但最佳交流性能是在48 kSPS和96 kSPS下實現的,其動態范圍和立體聲模式下的SNR均為典型的EIAJ標準、A加權、120 dB數字。在單聲道模式下,兩個通道同時異相組合,預計性能將提高3 dB。但是,對于寬帶應用,這些規格有些不切實際,因為它們是合成的,并且僅限于20 Hz至20 kHz帶寬。20 kHz以上不考慮帶外噪聲和雜散,部分原因是EIAJ標準、A加權濾波器和音頻行業規范定義。這種專門用于音頻測量的帶通濾波器模擬人耳頻率響應,與未濾波測量相比,結果高出 3 dB。
DDFS硬件演示平臺:使用AD1955進行正弦波重建
完整的DDFS使用兩個評估板實現,一個支持DSP處理器,另一個用于使用AD1955 DAC進行模擬信號重建。選擇第二代SHARC ADSP-21161N評估板是出于可用性原因,以及其易用性和精益配置,適用于任何音頻應用。ADSP-21161N仍在生產中,不久前設計用于支持工業、高端消費電子和專業音頻應用,提供高達110 Mips和660 MFlops或220 MMACS/s的能力。與最新一代SHARC處理器相比,ADSP-21161N的不同之處主要在于其短的3級指令流水線、片內1 Mb、僅三端口RAM和一組精簡的外設。精密音調發生器的最后也是最關鍵的階段基于AD1955評估板,該評估板必須忠實地從軟件NCO提供的樣本中重建模擬信號。該評估板帶有一個抗混疊濾波器(AAF),該濾波器針對音頻帶寬進行了優化,以滿足奈奎斯特準則,并具有幾個串行音頻接口以支持PCM/I2除了通常的 S/PDIF 或 AES-EBU 接收器之外,還有 S 和 DSD 數字流。The PCM/I2S串行鏈路連接器用于將AD1955 DAC板連接到ADSP-21161N EVB的串行端口1和3連接器(J)。兩塊板都可以配置為 I2S PCM 或 DSP 工作模式,采樣速率為 48 kSPS、96 kSPS 或 192 kSPS。DSP串行端口1生成雙通道DAC的數字輸入接口所需的左右通道數據、字選擇或L/R幀同步和SCK位時鐘信號。串行端口3僅用于生成DAC主時鐘MCLK,這是DAC插值濾波器和Σ-Δ調制器運行速度比輸入采樣頻率(48 kSPS)快256倍(默認情況下)所必需的。由于所有DAC時鐘信號均由DSP生成,因此將電路板原始的低成本愛普生時鐘振蕩器更改為Crystek的超低噪聲振蕩器CCHD-957。對于24.576 MHz的輸出頻率,其相位噪聲規格在1 kHz時可低至–148 dB/Hz。
在模擬輸出端,必須使用有源I/V轉換器將AD1955電流差分輸出保持在恒定共模電壓(典型值為2.8 V),以最大限度地降低失真。AD797等超低失真和超低噪聲高精度運算放大器用于此目的,也可用于處理模擬信號重建。由于兩個差分輸出由DSP單獨處理,因此選擇了具有AAF拓撲的立體聲輸出配置,而不是單聲道模式。該AAF是用LTspice XVII模擬的,結果如圖6所示。由于濾波器的最后一部分是無源濾波器,因此應增加一個有源差分緩沖級,就像最近推出的ADA4945一樣。這款低噪聲、超低失真、快速建立時間、全差分放大器是驅動任何高分辨率SAR和Σ-Δ型ADC的近乎完美的DAC伴侶。ADA4945具有相對較大的共模輸出電壓范圍和出色的直流特性,可提供出色的輸出平衡,有助于抑制偶次諧波失真產物。?
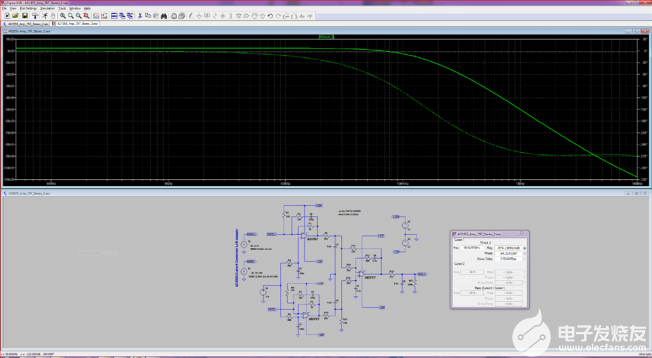
圖6.LTspice仿真AD1955 EVB三階抗混疊濾波器(立體聲配置)的頻率響應。
EVB三階濾波器的–3 dB截止頻率為76 kHz,在500 kHz時衰減僅為–31 dB。帶內平坦度非常好,但這種LP濾波器的帶外衰減必須得到認真改善,即使僅限于純重建音頻應用。這對于抑制DAC形狀的噪聲以及調制器時鐘頻率MCLK是強制性的。根據軟件DDS對單音發生器或任意波形發生器(用于復雜波形的AWG)的使用情況,AAF將針對帶外衰減或群延遲失真進行優化。作為一個實際的例子和比較,老式但著名的SRS DS360超低失真函數發生器設計有七階Cauer AAF,具有相似的采樣率。信號重建位于AD1862上,AD1862是一款面向數字音頻應用的串行輸入20位分段R-2R DAC。AD1862能夠支持高達768 kHz (×16 f)的20位字采樣速率S),并表現出出色的噪聲和線性度規格。其單端電流輸出使外部I-V轉換級可以選擇使用最佳放大器。
AD1955和SHARC DSP組合針對多個高分辨率SAR ADC進行了測試,例如AD4020,中間沒有外部選擇性無源濾波器。默認情況下,基本AD4020評估板除了板載ADA4807驅動器外沒有其他選擇。將ADC輸入偏置在V_REF/2共模電壓的簡單電路施加了300 Ω的相當低的輸入阻抗,需要信號隔離、交流耦合或使用外部差分放大器模塊,如EVAL-ADA4945-1。電路筆記CN-0513中描述的AD4020參考設計板是更好的選擇。它包括一個分立可編程增益儀表放大器(PGIA),可提供高輸入阻抗并接受±5 V差分輸入信號(G = 1)。雖然這些AD4020板及其SDP-H1控制器缺乏支持相干采樣采集的能力,但它們允許采樣的波形捕獲長度不錯,范圍可達1M。因此,具有選擇性窗口的長FFT是可能的,既能提供良好的頻率分辨率,又能提供低本底噪聲。例如,對于七項Blackman-Harris窗口,圖7所示的1 Mpts FFT圖說明了AD1955在990.059 Hz產生的正弦波下的失真水平。二次諧波是最大的失真分量和最大的雜散,在350 kHz帶寬內為–111.8 dBc。但是,當考慮806 kHz的整個ADC奈奎斯特帶寬時,SFDR受到DACΣ-Δ調制器和插值濾波器頻率及其二次諧波(384 kHz和768 kHz)的限制。
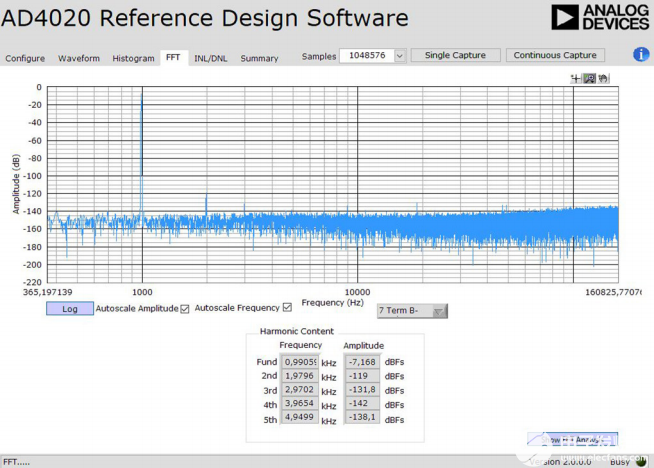
圖7.1 M 點 FFT 分析顯示,H2 低于 –111 dBc 時失真相當不錯,對于 1 kHz 輸入頻率,10 kHz 至 200 kHz 頻段的雜散最大。本底噪聲約為–146 dBFS。
在相同的條件下,對老式AD1862進行了測試試驗,其表現出略有不同的光譜行為。采用差分配置時,兩個時鐘頻率約為500 kSPS的20位DAC報告本底噪聲為–151 dBFS,THD為–104.5 dB,正弦輸出電平為12 V p-p,頻率為1.130566 kHz。AD4020奈奎斯特帶寬(806 kHz)上的SFDR接近106 dB,受三次諧波限制。基于兩個AD743低噪聲FET放大器的DAC重建濾波器與AD1955評估板的三階濾波器類似,但截止頻率為35 kHz,為–3 dB。
為了使其有效,基于DDS的發生器需要一個體面的濾波器,對于生成的直流至25 kHz CW信號頻率范圍,該濾波器能夠在約250 kHz下衰減大于100 dB。這可以通過六階切比雪夫甚至六階巴特沃茲LP濾波器來實現,以獲得完美的帶內平坦度。濾波器的階數將最小化,以限制模擬級的數量及其非理想性,如噪聲和失真。
結論
在標準評估板上進行的初步和開箱即用的測試表明,基于處理器的DDS技術可以實現具有頂級性能的傳統正弦波CW生成。–120 dBc諧波失真系數可以通過精心設計重建濾波器和模擬輸出緩沖級來滿足。基于DSP的NCO/DDS不僅限于產生單音正弦波。通過使用具有適當截止頻率且無需其他硬件更改的優化 AAF(貝塞爾或巴特沃斯),可以將相同的 DSP 和 DAC 組合偽裝成高性能 AWG 以產生任何類型的波形,例如,合成完全可參數化的多音正弦波,完全控制每個分量的相位和幅度以進行 IMD 測試。
由于浮點運算對于需要高精度和/或高動態范圍的應用至關重要,因此如今,低成本ADSP-21571或SoC ADSP-SC571(ARM和SHARC)等SHARC+ DSP處理器已成為實時處理的事實標準,總采樣速率高達10 MSPS。時鐘頻率為500 MHz,雙SHARC內核及其硬件加速器可以提供超過5 Gflops的計算性能,并提供大量內部專用SRAM,這是生成任何類型波形以及復雜分析處理任務所需的基本成分。這種類型的應用表明,系統地使用硬件可編程解決方案對于處理精密數字信號處理并不是強制性的。浮點處理器及其完整的開發環境允許從MATLAB等仿真器輕松快速地移植代碼,并通過ADI公司的CCES和VDSP++ C和C++編譯器及其全套仿真器和實時調試器進行快速調試。
審核編輯:郭婷
-
處理器
+關注
關注
68文章
19384瀏覽量
230492 -
DDS
+關注
關注
21文章
636瀏覽量
152787 -
信號發生器
+關注
關注
28文章
1478瀏覽量
108872
發布評論請先 登錄
相關推薦




 幾乎純DDS正弦波調發生器
幾乎純DDS正弦波調發生器











評論