01
說在前面的話
在 MEMS 慣性傳感器06 - 再說坐標系定義(導航坐標系與載體坐標系)這篇章中,在介紹導航坐標系與載體坐標系之間的姿態旋轉矩陣使用的是用歐拉角表示旋轉矩陣。
我們知道用來表示姿態的方法有: 1)歐拉角 2)方向余弦矩陣 3)四元數 4)等效旋轉矢量。 本篇我們介紹采用四元數表示姿態矩陣。 以下內容摘抄 《慣性導航》- 秦永元 姿態更新計算的四元數算法章節。
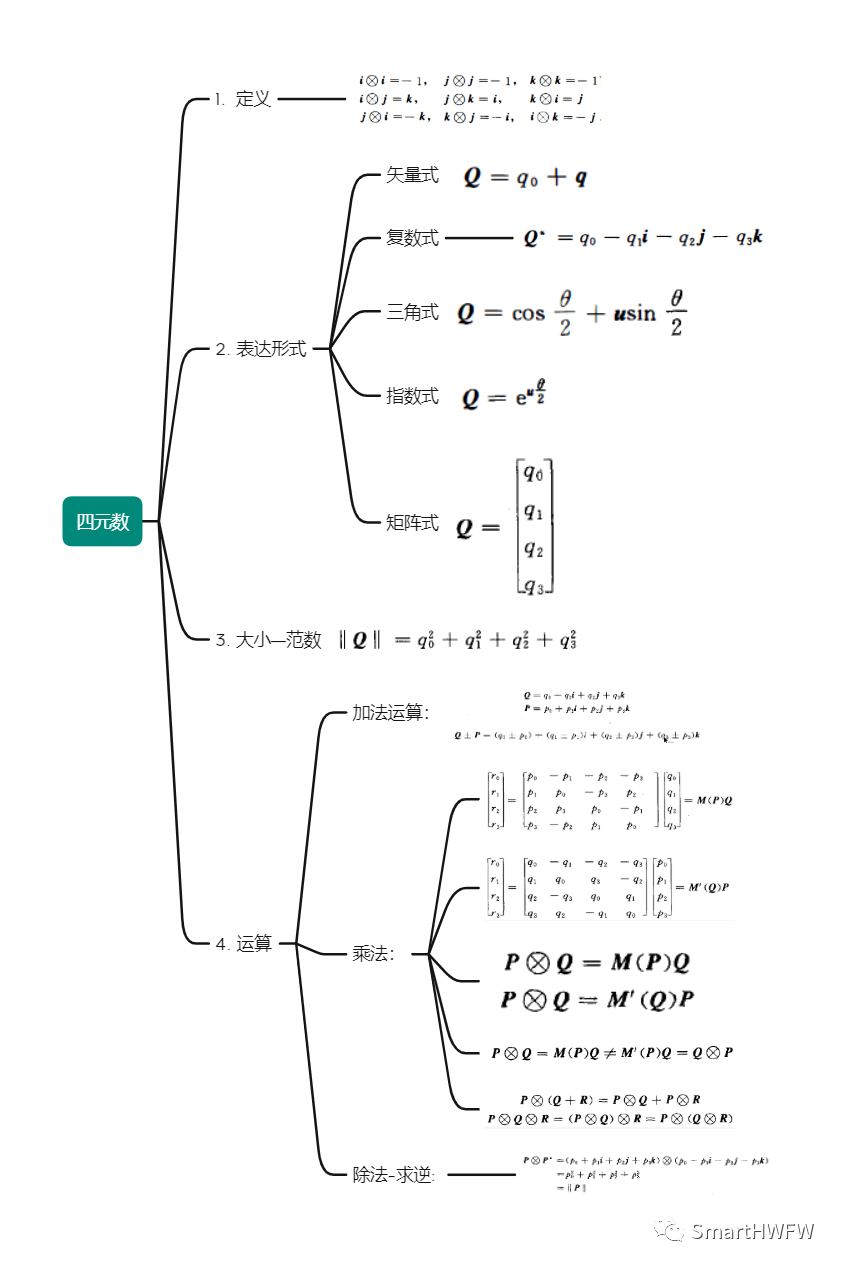
關于四元數的介紹和運算規則可以看前期文章。這里簡單的匯總一下:
02
四元數表示矩陣
三維空間的任意旋轉,都可以用繞三維空間的某個軸旋轉過某個角度來表示(即軸角,Axis-Angle表示方法)。這種表示方法里,Axis可用一個三維向量(x,y,z)來表示,θ可以用一個角度值來表示,直觀來講,一個四維向量(θ,x,y,z)就可以表示出三維空間任意的旋轉。
注意,這里的三維向量(x, y, z)只是用來表示axis的方向朝向,因此更緊湊的表示方式是用一個單位向量來表示方向axis,而用該三維向量的長度來表示角度值θ。這樣,可以用一個三維向量(θx, θy, θ*z)就可以表示出三維空間任意的旋轉,前提是其中(x,y,z)是單位向量。這就是旋轉向量(Rotation Vector)的表示方式。
Axis-Angle的表示方法還可以推導出另一種很常用的三維旋轉表示方法,叫四元數(Quaternion)。同上,假設(x, y, z)是axis方向的單位向量,θ是繞axis轉過的角度,那么四元數可以表示為 [cos(θ/2), xsin(θ/2), ysin(θ/2), z*sin(θ/2)]。
注意,這里可以推導出,用于表示旋轉的四元數向量也必須是單位向量。四元數的神奇之處在于,對于三維坐標的旋轉,可以通過四元數乘法直接操作,與上述旋轉矩陣操作可以等價,但是表示方式更加緊湊,計算量也可以小一些。捷聯慣導中的姿態更新實質上是如何計算四元數Q。



審核編輯:劉清
-
MEMS慣性傳感器
+關注
關注
1文章
18瀏覽量
7554
原文標題:MEMS 慣性傳感器07 - 四元數表示姿態矩陣
文章出處:【微信號:SmartHWFW,微信公眾號:SmartHWFW】歡迎添加關注!文章轉載請注明出處。
發布評論請先 登錄
相關推薦
如何更改mpu6050的DMP使坐標系跟原坐標系一致?
介紹坐標系和機器人之間的紐帶即連桿坐標系
同步旋轉坐標系下的數學模型
OPENGL坐標系介紹 世界坐標系和當前繪圖坐標系區別

自動駕駛各個坐標系

自動駕駛中的各種時空坐標系

三坐標如何建立坐標系?

深度剖析機器人的四大坐標系




 介紹導航坐標系與載體坐標系之間的姿態旋轉矩陣
介紹導航坐標系與載體坐標系之間的姿態旋轉矩陣










評論