ABS(X)
總和
REAL_MIN…REAL_MAX 0 … REAL_MAX
SQRT(X)
平方根
0 … REAL_MAX 0 … REAL_MAX
SIN(X)
正弦
REAL_MIN…REAL_MAX -1 … +1
COS(X)
余弦
REAL_MIN…REAL_MAX -1 … +1
TAN(X)
正切
REAL_MIN…REAL_MAX REAL_MIN…REAL_MAX
ACOS(X)
反余弦
-1 … +1 0 … +180
ATAN2(Y,X)
反正切
REAL_MIN…REAL_MAX -180 … +180
絕對值 ABS(X) 計算 X 的總和。
示例:
B = -3.4
A = 5*ABS(B) ;A=17.0
平方根 SQRT(X) 計算 X 的平方根。
示例:
A = SQRT(16.0801) ;A=4.01
正弦 SIN(X) 計算角度 X 的正弦。
示例:
余弦 COS(X) 計算角度 X 的余弦。
示例:
A = SIN(30) ;A=0,5
B = 2*COS(45) ;B=1.41421356
正切 TAN(X) 計算角度 X 的正切。
示例:
以下總和的正切無窮:
C = TAN(45) ;C=1.0
? ±90°
? +90° + k*180° (其中 k = ± 整數)
如果嘗試一個這樣的值,這將導致錯誤信息。
反余弦 ACOS(X) 是 COS(X) 的反函數。
示例:
A = COS(60) ;A=0.5
B = ACOS(A) ;B=60
反正弦 對于 SIN(X) 的反函數反余弦,沒有預定義函數。但是,基于公式 SIN(X) =
COS(90°-X) 可以很容易就計算出反正弦。
示例:
A = SIN(60) ;A=0.8660254
B = 90-ACOS(A) ;B=60
反正切
角度正切的定義是直角三角形的鄰邊 (X) 除以對邊 (Y)。如果兩個側邊的長度已知,則可以用反正切計算鄰邊和斜邊之間的角度。
對于全圓,起決定性作用的是 X 和 Y 的正負號是什么。如果只考慮商,則用反正切只能計算 0° 和 180° 之間的角度。通常,這在袖珍計算器時也是如此:正值的反正切得出一個 0° 和 90° 之間的角度。負值的反正切得出一個 90° 和 180° 之間的角度。
通過用正負號指定 Y 和 X 明確地確定了位于該角度中的四分之一圓。由此也可以計算四分之一圓 III 和 IV 中的角度。
示例: A = ATAN2(0.5,0.5) ;A=+45 B = ATAN2(0.5,-0.5) ;B=+135 C = ATAN2(-0.5,-0.5) ;C=-135 D = ATAN2(-0.5,0.5) ;D=-45
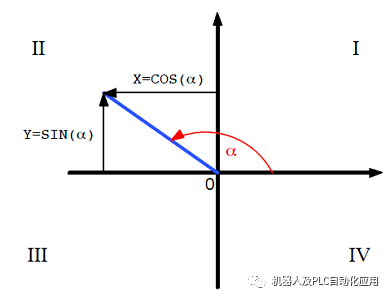
在函數 ATAN(Y,X) 中使用 X 和 Y
審核編輯:劉清
-
ABS
+關注
關注
2文章
162瀏覽量
34658 -
計算器
+關注
關注
16文章
437瀏覽量
37406
原文標題:KUKA: 數學標準功能
文章出處:【微信號:gh_a8b121171b08,微信公眾號:機器人及PLC自動化應用】歡迎添加關注!文章轉載請注明出處。
發布評論請先 登錄
相關推薦
HAL庫和標準庫的區別 HAL庫與CMSIS的關系
光電效應的數學模型及解析
傅里葉變換的數學原理
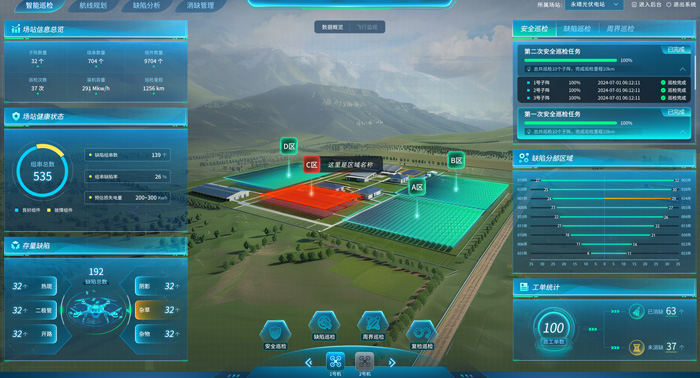
無人機電力巡檢系統的功能淺析
什么是汽車ISO 26262功能安全標準?

功能安全標準在汽車芯片領域的應用

神經網絡在數學建模中的應用
當AI與數學同時走下神壇

工業控制器的制作與數學的關系
三相SVPWM電壓型逆變器的數學模型
淺析消防設備電源監控系統設計及應用




 淺析KUKA數學標準功能
淺析KUKA數學標準功能











評論