數字電路中的組合邏輯電路的設計與分析過程相反，本文小編主要跟大家介紹一下關于組合邏輯電路的設計步驟，順便回顧一下組合邏輯電路的分析方法。

組合邏輯電路的設計，通常以電路簡單，所用器件最少為目標。在前面所介紹的用代數法和卡諾圖法來化簡邏輯函數，就是為了獲得最簡的形式，以便能用最少的門電路來組成邏輯電路。但是，由于在設計中普遍采用中、小規模集成電路（一片包括數個門至數十個門）產品，因此應根據具體情況，盡可能減少所用的器件數目和種類，這樣可以使組裝好的電路結構緊湊，達到工作可靠而且經濟的目的。

組合邏輯電路設計步驟

在教學過程中，學生對組合邏輯電路的設計過程覺得比較難。不知從何人手。筆者經過多年的教學，總結出組合邏輯電路的設計步驟如下，并舉例說明。

組合邏輯電路設計是根據給出的邏輯問題，設計出一個組合邏輯電路去滿足提出的邏輯功能要求。

組合邏輯電路的設計步驟如下：

1、仔細分析設計要求。做出輸入，輸出變量的邏輯規定。根據給出的條件，列出真值表。

2、將真值表寫入卡諾圖。化簡。卡諾圖法化簡是一種很方便、很準確的化簡方法，只要有足夠的細心，化簡結果就不會有問題。

3、畫邏輯電路圖。卡諾圖法化簡后得到最簡的與一或表達式。若需要其他的形式，可先轉化后再作圖。下面用實際例子來詳細分析。

例：某單位舉辦游藝晚會，男士持紅票入場。女士持黃票入場。持綠票不管男女均可入場，試用與非門設計這個游藝晚會入場放行的邏輯控制電路。

第一步：由題意找出輸入、輸出變量，列真值表。題中出現男、女、黃票、紅票、綠票共五個變量。有人會建議設五個輸入變量，可是若細細想來。可看出男、女為表示對立的變量。可用一個變量A的兩種狀態來表示。可設A=O為女，A=I表示男。

剩下的紅票、黃票、綠票分別用B、C、D來表示，即B=I為持紅票。B=O為沒有紅票；C=1為持黃票，C=0為沒有黃票；D=l為持綠票，D=0為沒有綠票；設L為輸出變量，L=1可入場，L=0不可入場。根據上述邏輯規定，按題意列出真值表如附表。

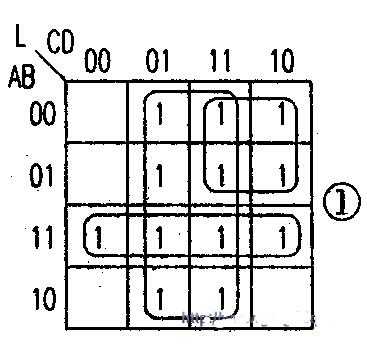
第二步：將真值表寫入卡諾圖，化簡。在畫包圍圈的過程中（如圖l所示）。

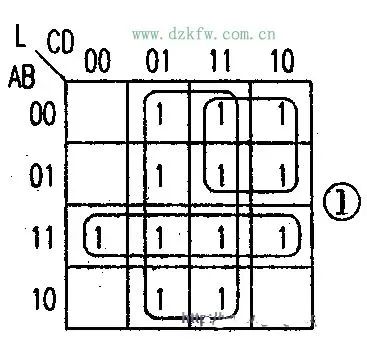
要注意以下幾點：

1、包圍圈越大越好（合并后得到的乘積項中因子最少）。

2、包圍圈的個數越少越好（表達式乘積項項數最少）。

3、同一個“1”方塊可以被圈多次（因為A+A=A，對邏輯函數的正確性無影響）。

4、每個圈要有新的成分，如果某一圈中所有的“1”方塊均被別的包圍圈包圍，則此圈所表示的乘積項是多余的。

5、畫包圍圈時，可先圈大，后圈小。

6、不要遺漏任何方塊（否則函數會出錯）。

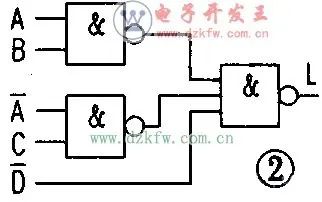
將各圈寫成邏輯函數表達式的形式，并化成題中要求的形式，即得到：L=D+AB+AC=DABAC綜上所述。可看出設輸入、輸出變量是邏輯電路設計的第一關鍵。

只有變量設得恰當，才能根據題意順利地列出正確的真值表。卡諾圖法化簡是第二關鍵，不過只要按照化簡規則。仔細分析作答，并化簡成題里所需要的形式，然后根據邏輯表達式畫出相應的邏輯電路圖即可。

延伸閱讀：組合邏輯電路的分析步驟

1、分析組合邏輯電路的步驟大致如下：

已知邏輯圖→寫邏輯式 →運用邏輯代數化簡或變換→ 列邏輯狀態表→ 分析邏輯功能

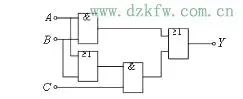
例：某一組合邏輯電路如下圖所示，試分析其邏輯功能。

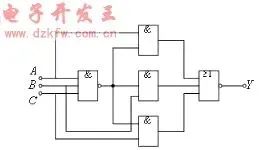
解：（1）由邏輯圖寫出邏輯式，并化簡

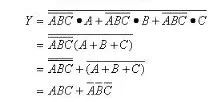
（2）由邏輯式列出邏輯狀態表（下表）

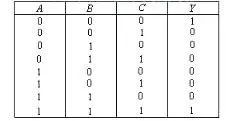
（3）分析邏輯功能

只當A，B，C全為“0”或全為“1”時，輸出Y才為“1”，否則為“0”。故該電路稱為“判一致電路”，可用于判斷三個輸入端的狀態是否一致。

2、綜合組合邏輯電路的步驟大致如下：

已知邏輯要求→ 列邏輯狀態表→ 寫邏輯式→ 運用邏輯代數化簡或變換→ 或邏輯圖

例：試設計一邏輯電路供三人（A，B，C）表決使用。每人有一電鍵，如果他贊成，就按電鍵，表示“1”；如果不贊成，不按電鍵，表示“0”。表決結果用指示燈來表示，如果多數贊成，則指示燈亮，Y=1；反之則不亮，Y=0。

解：

（1）由題意列出邏輯狀態

共有八種組合，Y=I的只有四種。邏輯狀態表如下表所示。

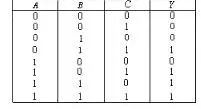
（2）由邏輯狀態表寫出邏輯式

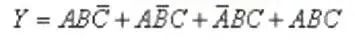
（3）變換和化簡邏輯式

對上式應用邏輯代數運算法則7，8，14進行變換和化簡：

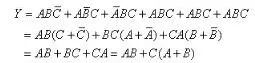
（4）由邏輯式畫邏輯圖

由上式畫出的邏輯圖如下圖所示。

審核編輯：湯梓紅