前言:
在2020年8月,我曾經(jīng)發(fā)過基于SOGI二階積分器原理的的鎖相環(huán)的實(shí)現(xiàn)和仿真模型,可見:《一種應(yīng)用于三相電網(wǎng)的雙SOGI鎖相環(huán)實(shí)現(xiàn)方法和仿真》。但是基于SOGI的特性還可以實(shí)現(xiàn)鎖頻環(huán),可以自動的適應(yīng)電網(wǎng)頻率變化,大大的提升了基于SOGI原理的鎖相環(huán)的性能。
SOGI僅在諧振頻率中心才能是0dB增益,這意味著當(dāng)電網(wǎng)頻率改變,SOGI濾波器的諧振中心頻率沒有改變時,會導(dǎo)致SOGI輸出的正交波形與輸入波形相比會失真,導(dǎo)致鎖相不準(zhǔn)確。因此為了解決這問題,就需要獲取電網(wǎng)的頻率變化信息,然后同步的調(diào)整SOGI濾波器的諧振中心頻率,來實(shí)現(xiàn)最佳的鎖相性能。
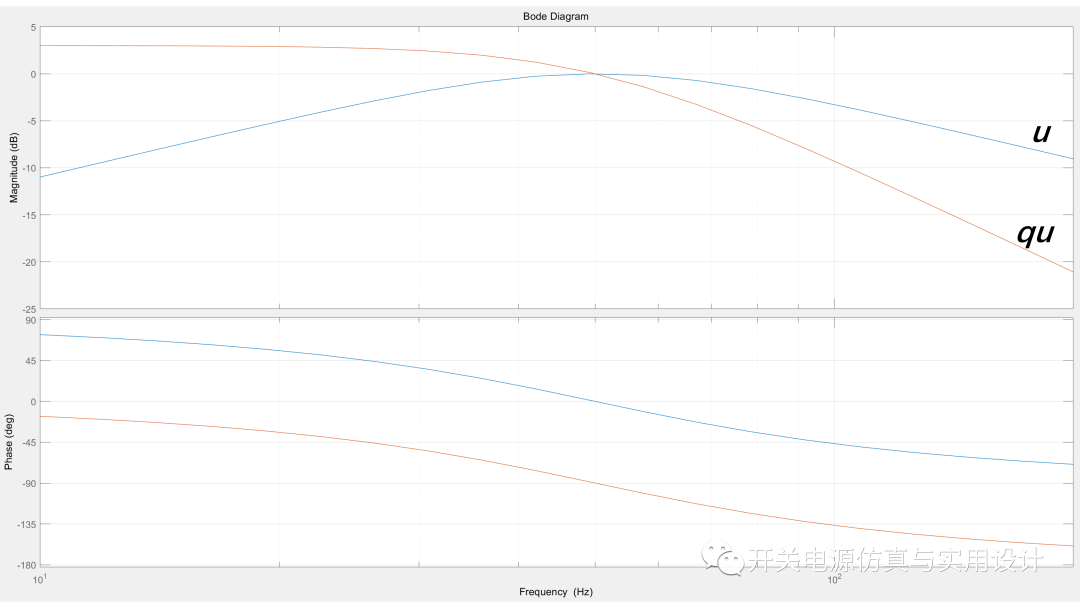
(SOGI的頻率響應(yīng))
觀察二階SOGI正交信號發(fā)生器,要使它能自動調(diào)節(jié)頻率wn,首先就是分析誤差信號e,并研究如何利用該誤差信號來自動調(diào)節(jié)SOGI的諧振中心頻率。
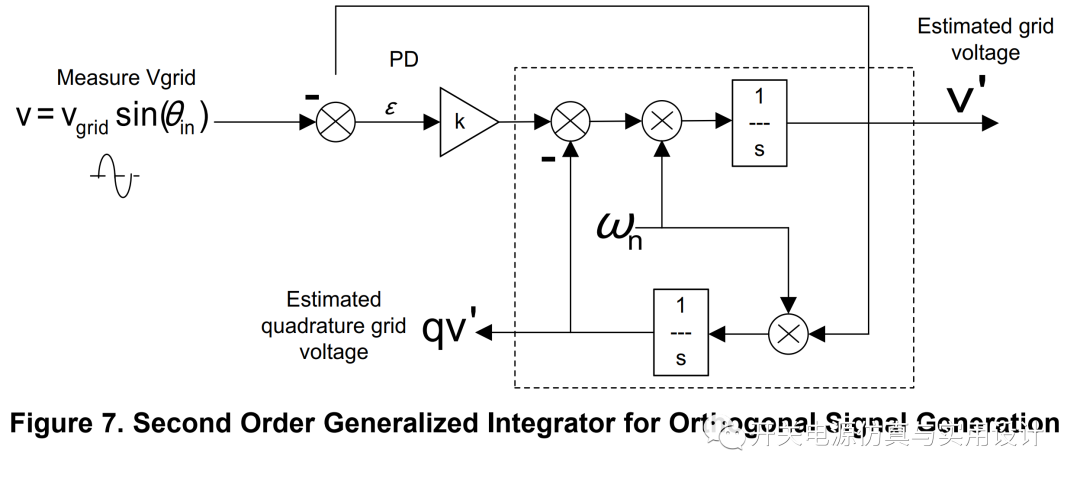
(SOGI)
從輸入信號v到誤差信號e的傳遞函數(shù)為:
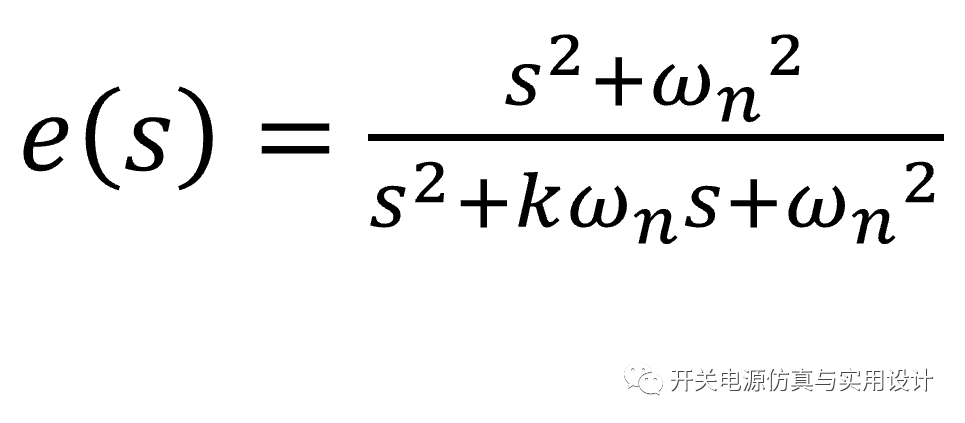
(誤差信號傳遞函數(shù))
這個誤差的傳遞函數(shù)其實(shí)是一個二階陷波濾波器,在其諧振中心頻率出的增益為零。而且該傳遞函數(shù)還有個有趣的特征,當(dāng)輸入信號的頻率w從比SOGI諧振中心頻率wn低變?yōu)楦邥r,輸出信號的相角會發(fā)生180°跳變,下面將用這個特性來比較兩個頻率的值。
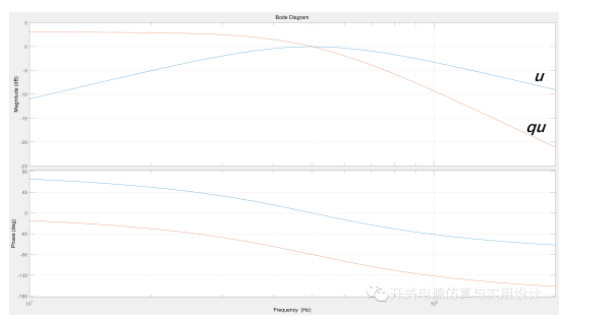
為了研究e(s)和qu(s)之間的關(guān)系,下圖把他們放在一起進(jìn)行分析。可以看出當(dāng)輸入頻率比SOGI的諧振中心頻率wn低時,信號e和qu是同相的,反之,當(dāng)輸入頻率高于SOGI的諧振中心頻率wn時,信號e和qu是反相的。
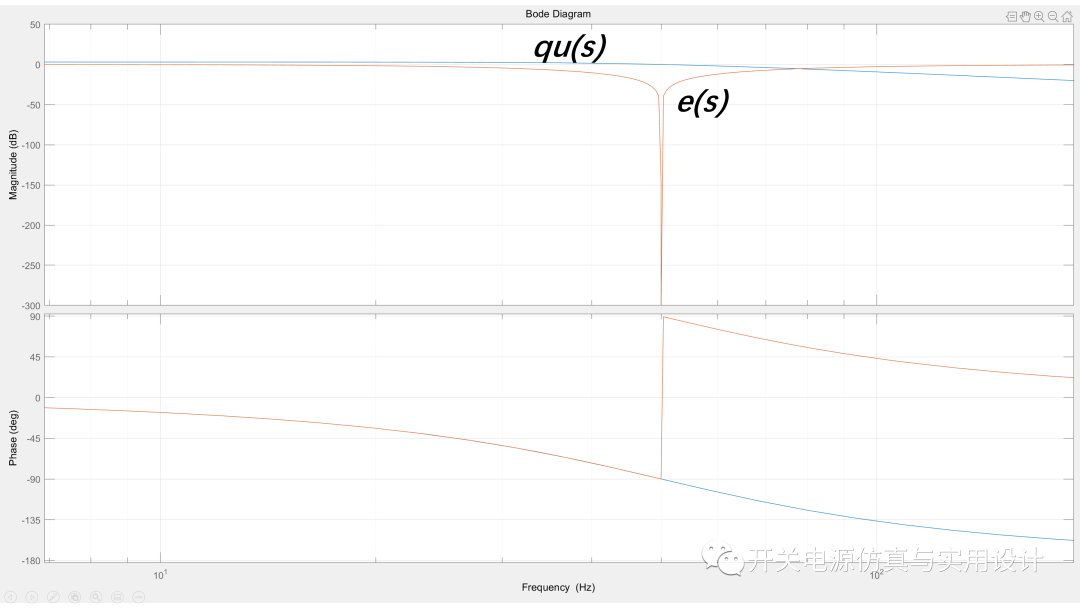
(誤差信號傳遞函數(shù)的頻率響應(yīng))
因此,頻率誤差變量ef可以定義為qu和e的乘積,正如上圖看到的信息。當(dāng)輸入頻率低于wn時,ef的平均值大于零,兩者相等時等于零,當(dāng)輸入頻率高于wn時,該誤差小于零。所以利用這特性可以設(shè)計一個非常簡單的鎖頻環(huán),可見下圖:
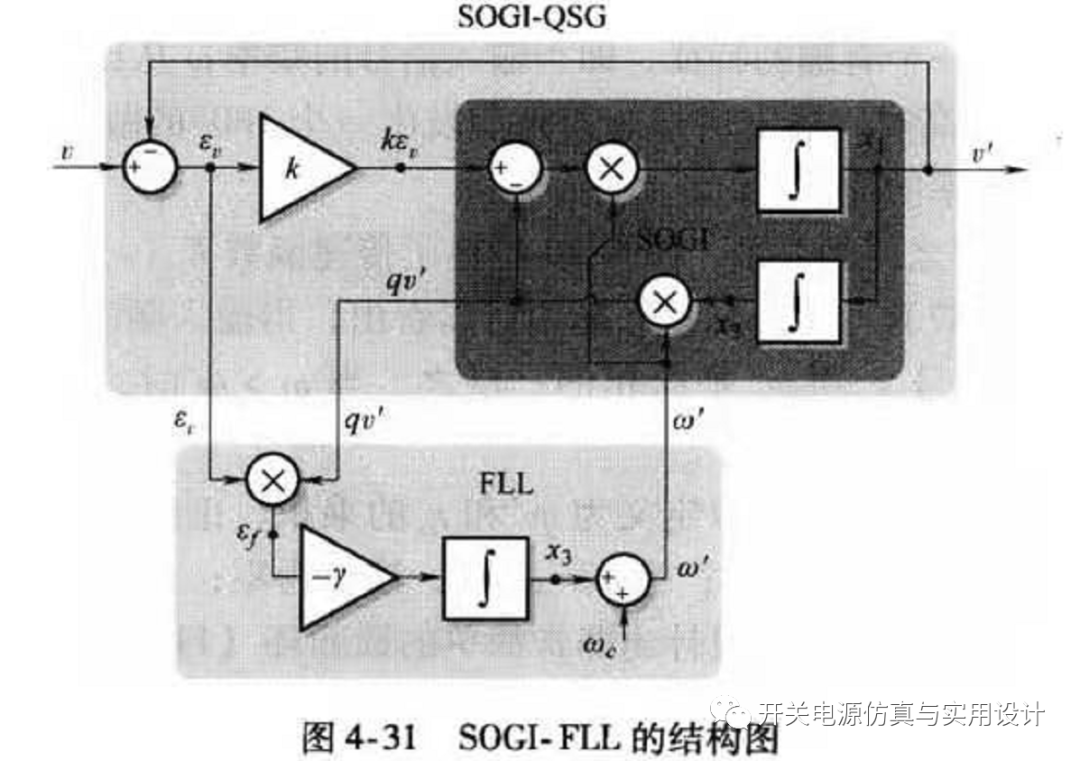
(SOGI FLL結(jié)構(gòu))
在這個環(huán)路中,利用負(fù)向增益r的積分再加上電網(wǎng)頻率的前饋使SOGI的諧振中心頻率與輸入頻率一致,使ef的直流分量控制到零,實(shí)現(xiàn)鎖頻。因此可以將SOGI PLL和FLL結(jié)合起來,實(shí)現(xiàn)對電網(wǎng)頻率擾動的自動補(bǔ)償和跟蹤,同步調(diào)整SOGI的諧振中心頻率wn,提升鎖相的可靠性,可見仿真模型:
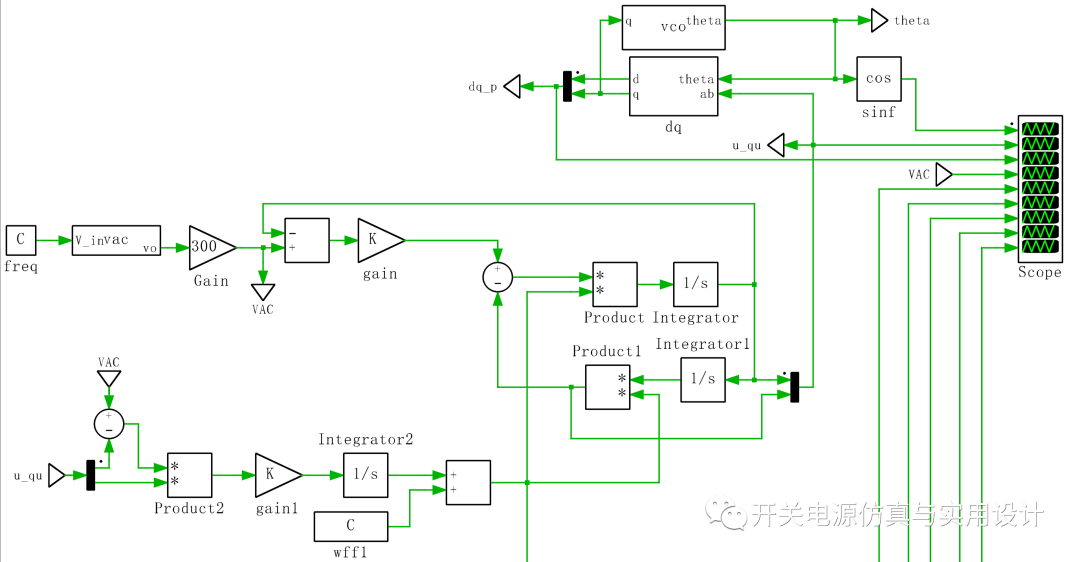
(SOGI FLL仿真模型)
運(yùn)行測試,隨意改變電網(wǎng)頻率和幅值,鎖相環(huán)都能快速鎖相:
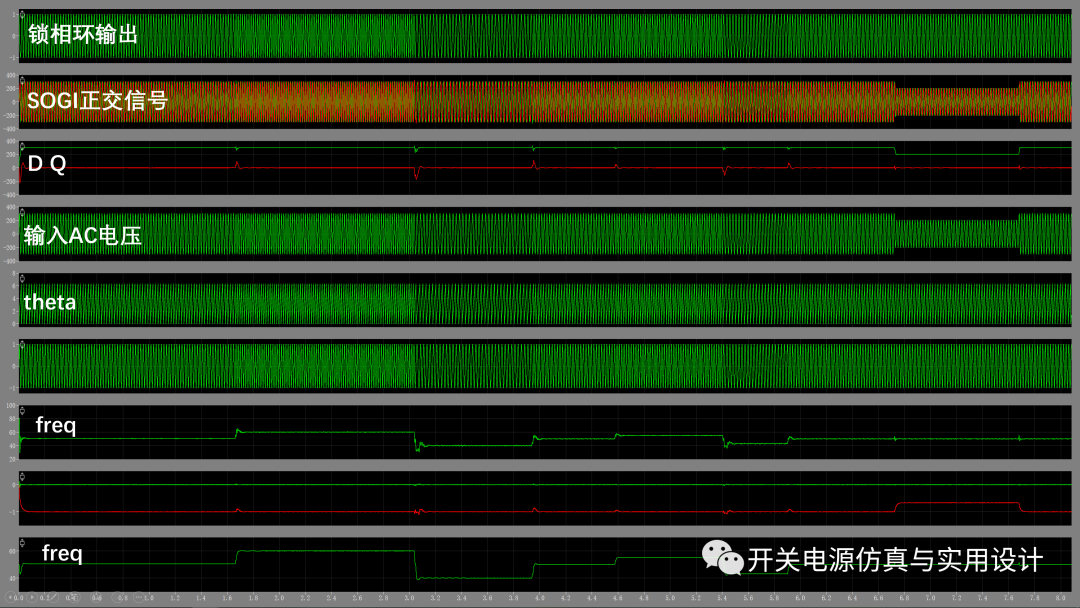
(SOGI FLL在理想AC輸入情況下仿真)
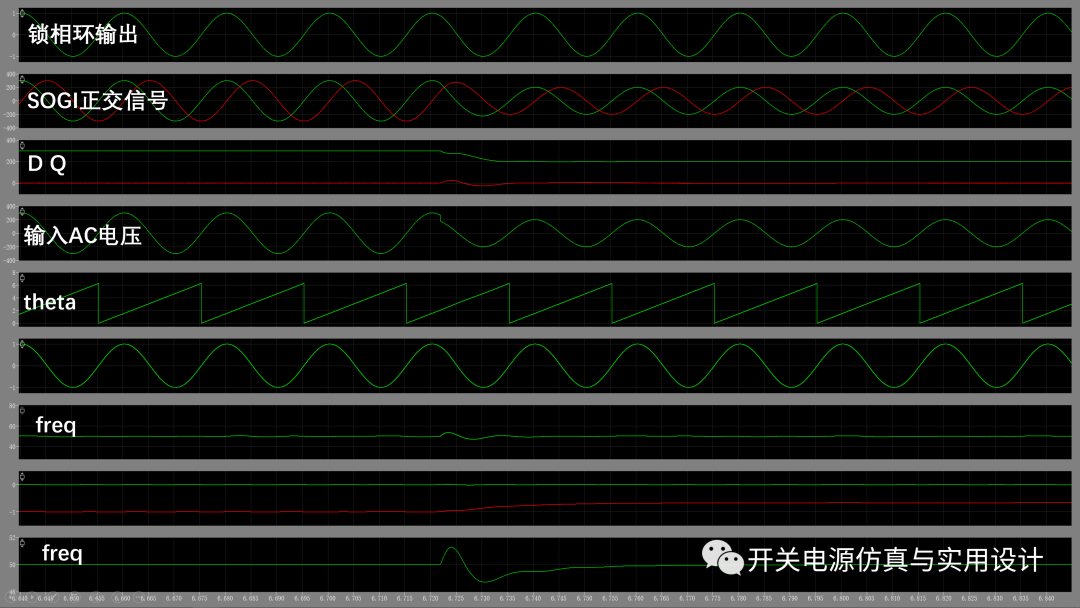
(SOGI FLL在理想AC輸入情況下仿真)
為了測試SOGI鎖頻環(huán)在電網(wǎng)高次諧波注入下的性能,我特別搭建了多次諧波注入的模型,可見,1~10次隨意改變:
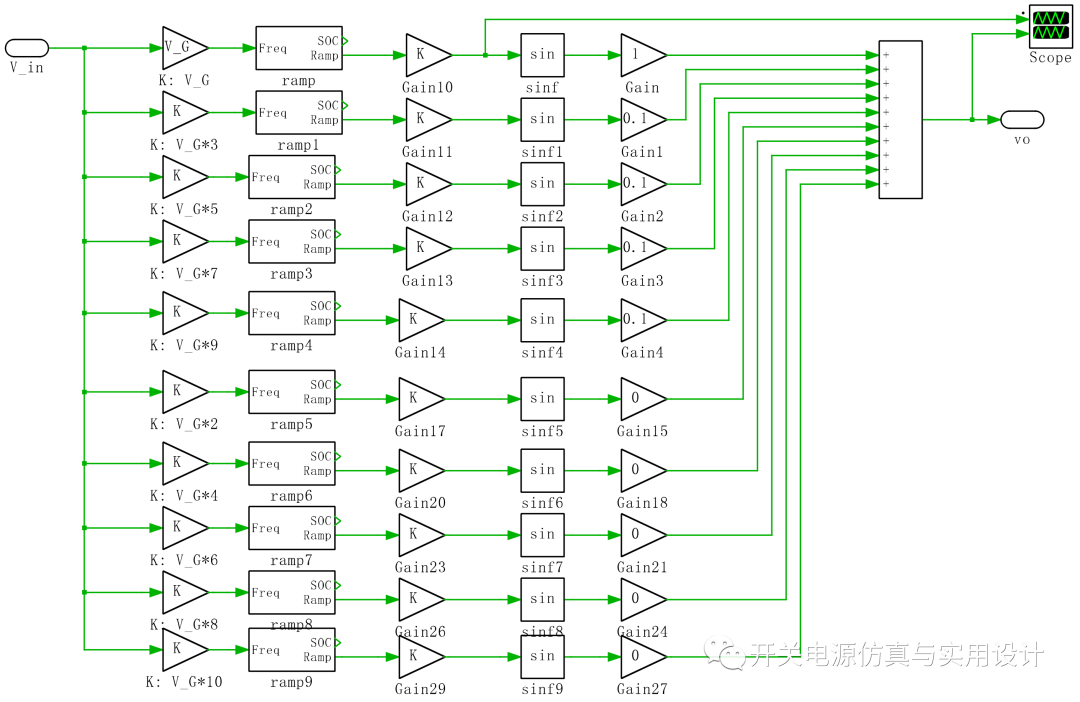
(諧波生成方法)
運(yùn)行測試:即使在高次諧波注入情況下,SOGI鎖頻環(huán)依然能很好穩(wěn)定的鎖相,性能確實(shí)不錯:
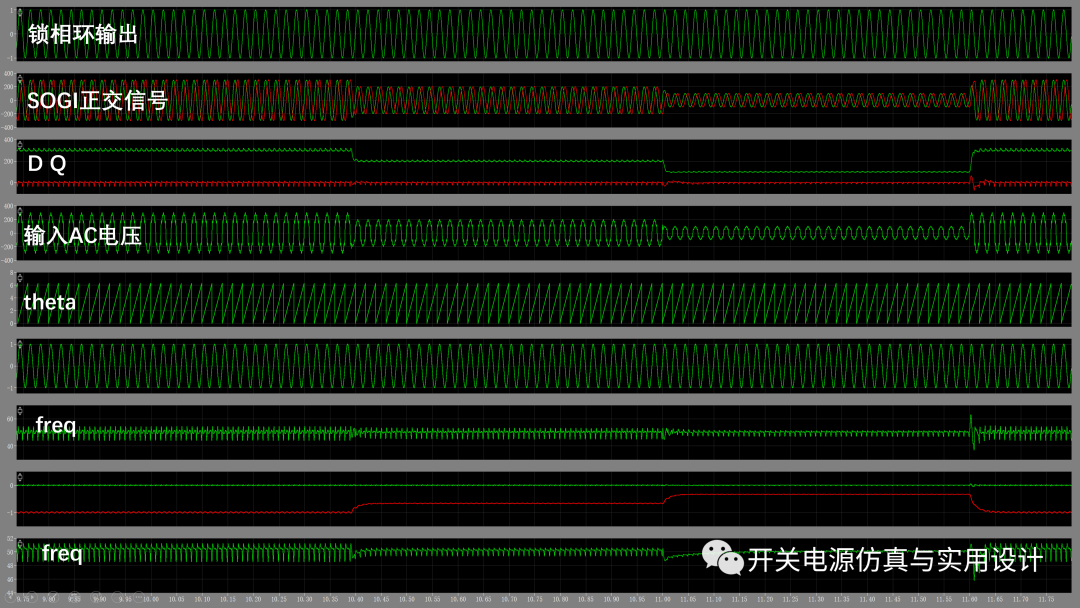
(SOGI FLL在非理想AC輸入情況下仿真)
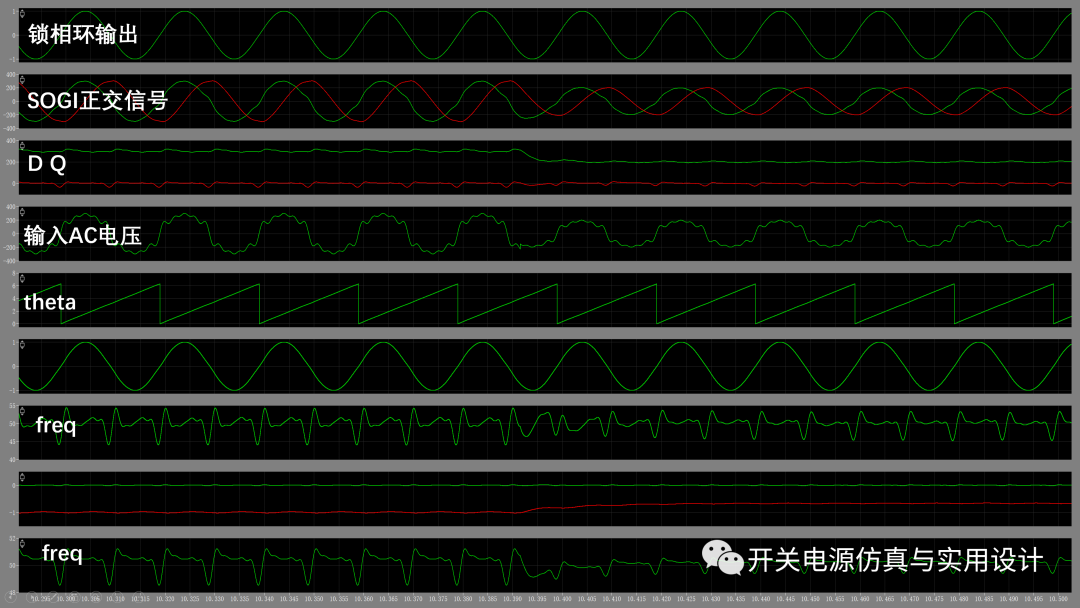
(SOGI FLL在非理想AC輸入情況下仿真)
小結(jié):參考書中SOGI鎖頻環(huán)的實(shí)現(xiàn)方法,搭建了單相SOGI FLL模型,并模擬電網(wǎng)存在高次諧波干擾下的鎖頻環(huán)性能,均達(dá)到了令人滿意的效果。
-
濾波器
+關(guān)注
關(guān)注
161文章
7846瀏覽量
178414 -
頻率
+關(guān)注
關(guān)注
4文章
1514瀏覽量
59276 -
諧振頻率
+關(guān)注
關(guān)注
2文章
45瀏覽量
16987
發(fā)布評論請先 登錄
相關(guān)推薦
基于SOGI濾波器的單相鎖頻環(huán)仿真案例
針對直流偏移和諧波干擾的單相鎖相環(huán)
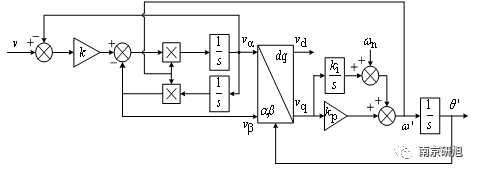
單相半橋逆變器仿真技巧資料下載
單相單位功率因數(shù)整流simulnk仿真 精選資料分享
單相整流軟件鎖相環(huán)(PLL)simulink仿真及鎖相環(huán)實(shí)物模塊制作 精選資料分享
TEMS鎖頻測試說明
基于雙二階廣義積分鎖頻環(huán)的光伏并網(wǎng)發(fā)電系統(tǒng)仿真研究_張占鋒
復(fù)雜電網(wǎng)工況下三相并網(wǎng)逆變器的鎖頻環(huán)技術(shù)_李建文
鎖頻環(huán)和鎖相環(huán)區(qū)別
單相全橋逆變器滯環(huán)雙閉環(huán)控制simulink仿真的詳細(xì)資料說明
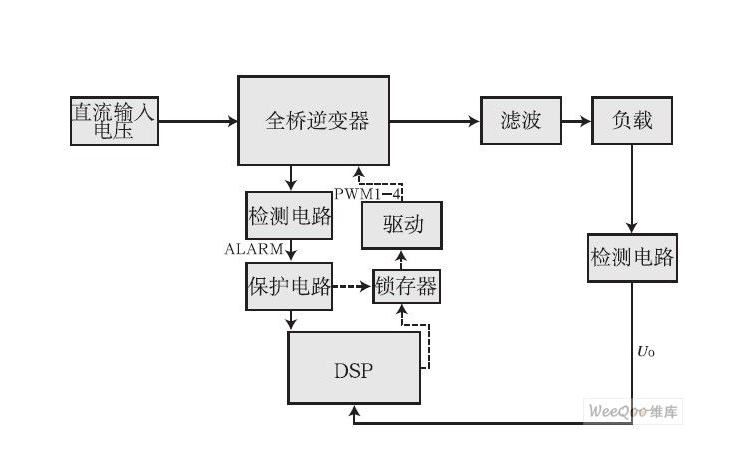




 SOGI原理的單相鎖頻環(huán)的原理和仿真
SOGI原理的單相鎖頻環(huán)的原理和仿真










評論