引子

自打牛頓-萊布尼茨(Newton-Leibniz)發明微積分后, 整個數學和物理世界就不太平了, 早在1655年Wallis就開始研究了橢圓(ellipse)的弧長, 并且牛頓和Wallis都發表了關于橢圓弧長的級數表達式, 其次單擺周期的求解, 這些問題困擾了一代又一代人。

1679年雅各布·伯努利(Jacob Bernoulli)對彈性桿的研究中也遇到了橢圓積分, 并且得到了一個簡單的橢圓積分的例子：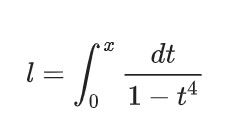

早期這個積分也叫雙扭線積分(lemniscate integral), 并且伯努利也意識到了這個積分不簡單, 并不能用初等函數表達。

1750年左右, 歐拉(Euler)發展了橢圓積分, 如橢圓積分的加法定理(Elliptic Integral Addition Theorems)和蘭登變換, 以加法定理為例說明：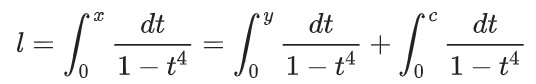

其中積分上限滿足：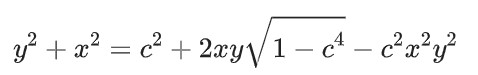

并且歐拉給出了其幾何意義。

1785年拉格朗日(Lagrange)就發表了一篇關于橢圓積分的文章, 其中用到了AGM(Arithmetic-Geometric Mean,算術幾何平均數), 接著高斯獨立的發現了AGM, AGM讓橢圓積分的數值計算變得容易。

接著到了1826年勒讓德(Legendre)開始全面論述了橢圓積分并著作《橢圓函數論》, 將橢圓積分歸為三大類, 現稱為橢圓積分的勒讓德形式(elliptic integral in Legendre's form)：

本章節主要討論和橢圓函數濾波器相關的第一類橢圓積分：

第一類不完全橢圓積分(incomplete elliptic integral of the first kind)：三角形式:

到了(1829年)雅可比(Carl.Gustav.Jacob.Jacobi)和阿貝爾(N.H. Abel)時代, 橢圓函數理論發生了質的變化, 這里最主要的貢獻是橢圓積分反演, 也就是說我們不去直接研究橢圓積分, 而是研究橢圓積分的逆, 即原橢圓積分的積分上限為函數值, 積分值為自變量, 同時也發現了其逆的雙周期性質。

對于第一類橢圓積分, 我們和定義正弦函數一樣定義雅可比橢圓正弦函數滿足如下等式：

為了解決函數的多值性所帶來困擾, 黎曼把思考維度又提升一個層次, 將復平面拓展為許多葉的曲平面上, 思考維度從二維上升到了三維, 這時出現了黎曼曲面的概念了, 這里開辟了數學新戰場--拓撲學。

當然, 以上是對橢圓積分的知識的一個簡單漸進式的梳理。對于濾波器設計而言, 實際上我們關心第一類橢圓積分的一些性質和計算方法, 這里主要介紹雙周期性和其數值計算方面。

若對橢圓積分和橢圓函數感興趣的同學可以閱讀扶教授的講座筆記《橢圓積分和橢圓函數講座回顧》。

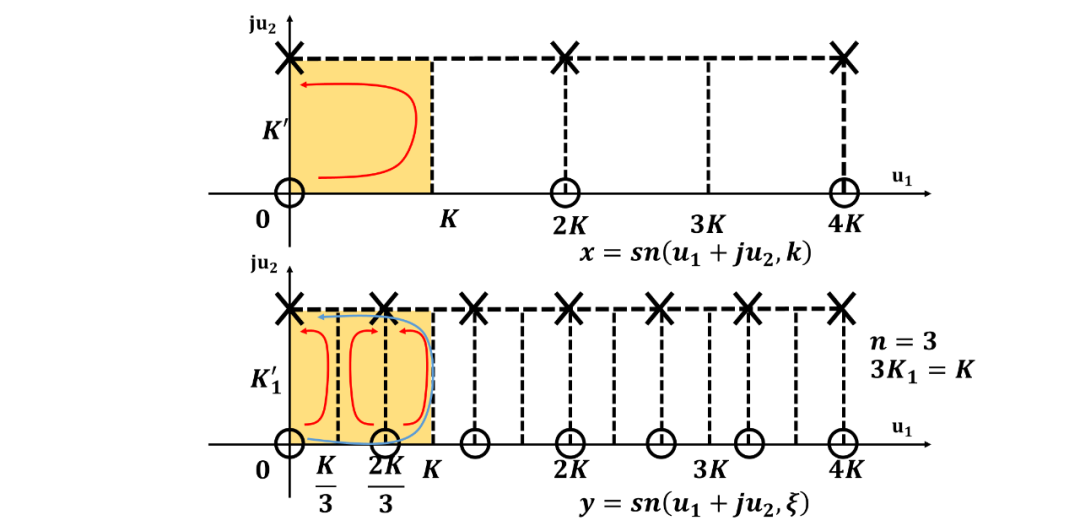
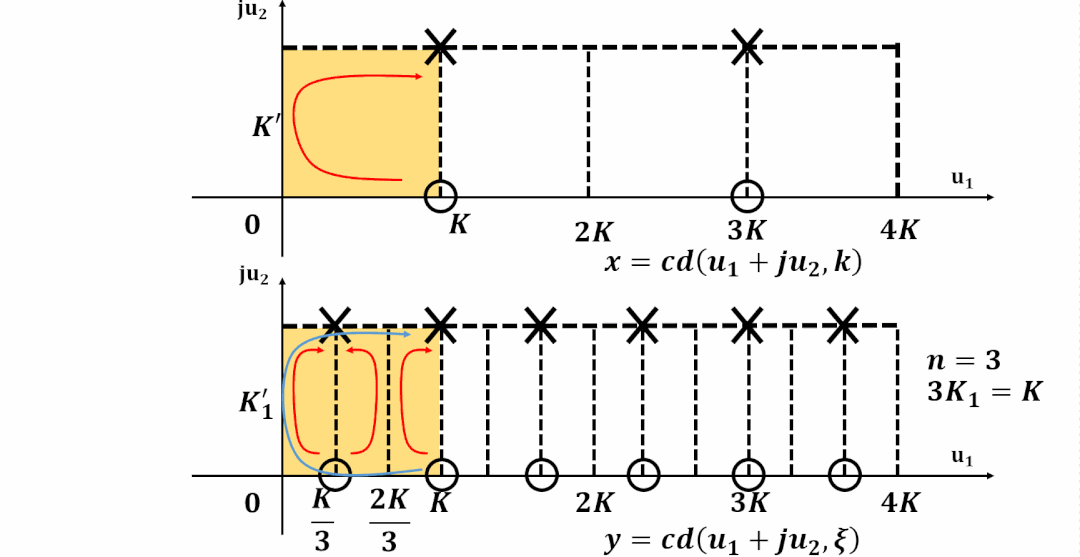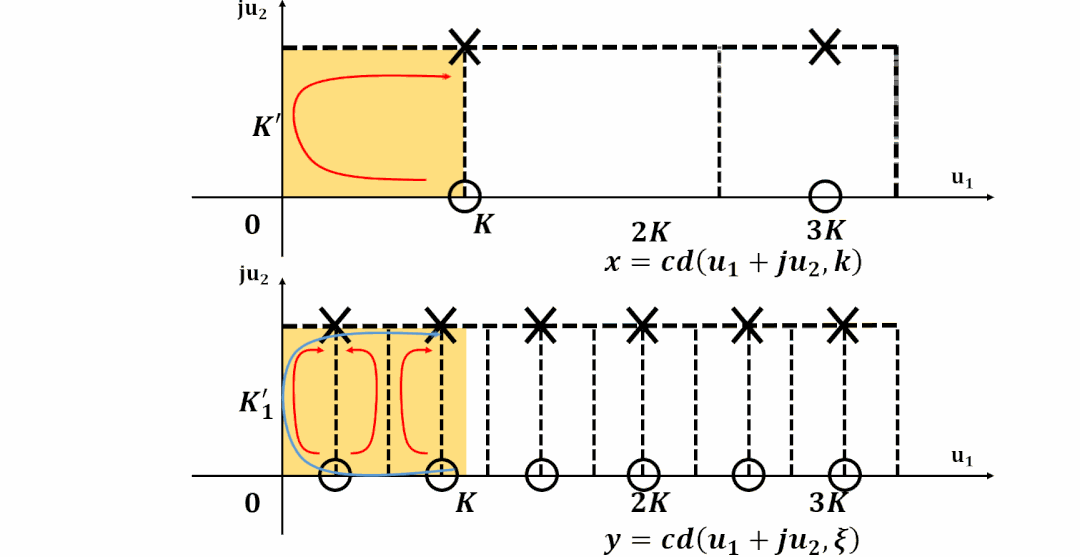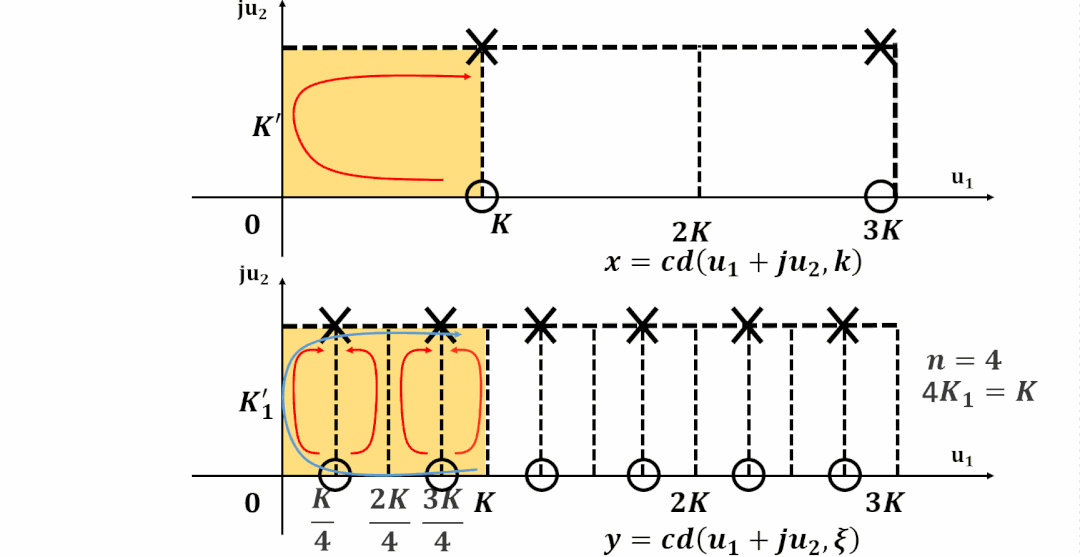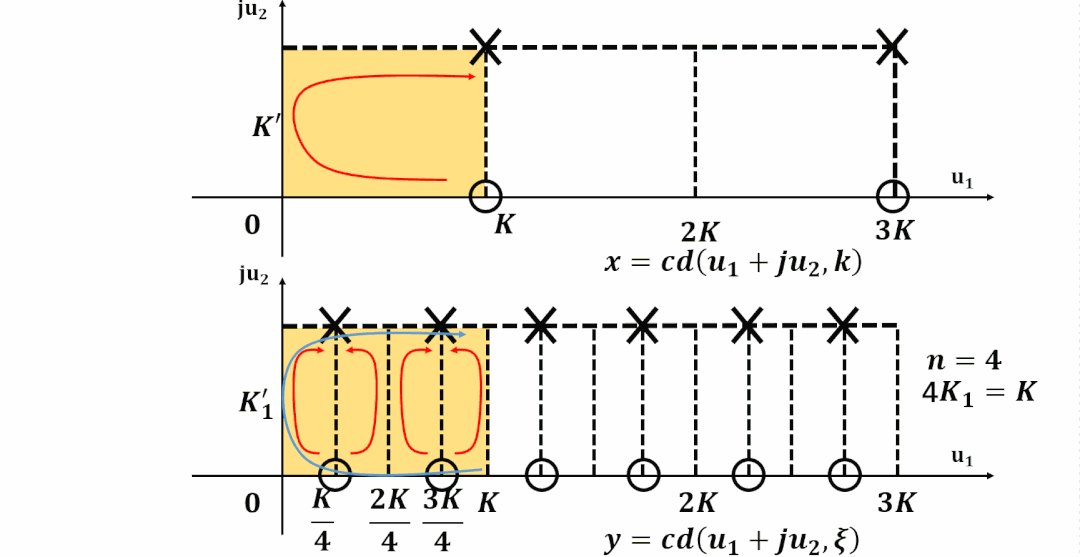
理解雅可比函數的雙周期性

數域的拓展

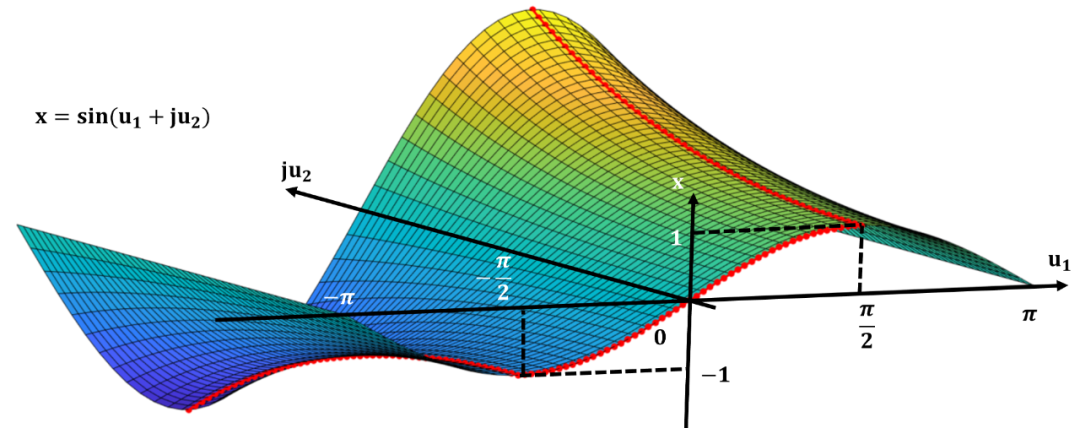
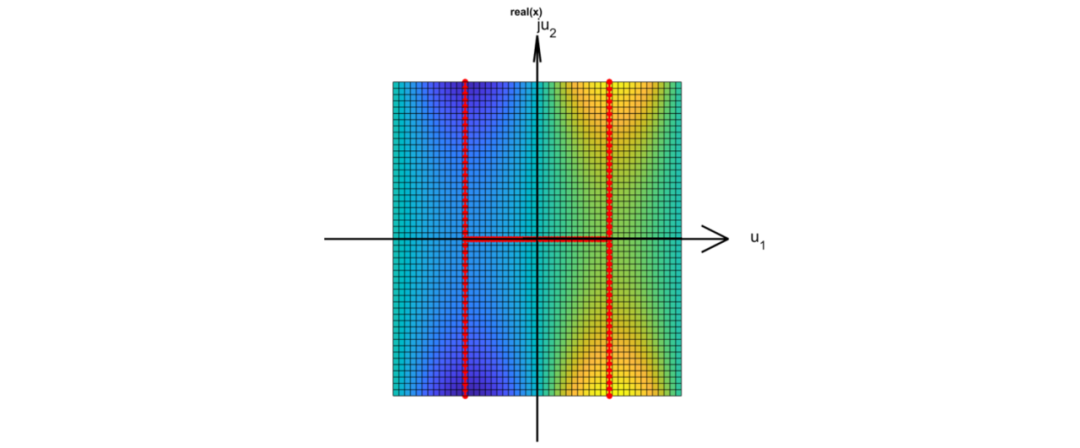
試想一下一個螞蟻在這個復平面上爬, 那么如何爬, 其高度可以連續的從低到高?下圖就展示了這一過程:

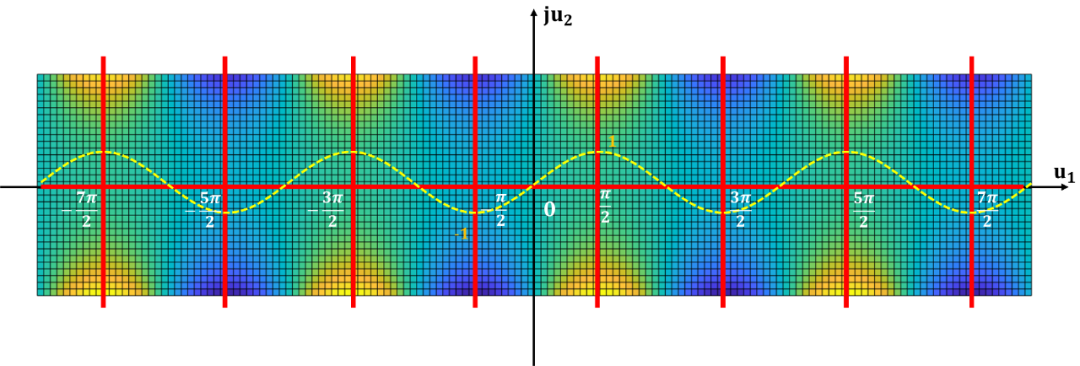
單周期

再簡化一下, 得到：

其周期帶如下：

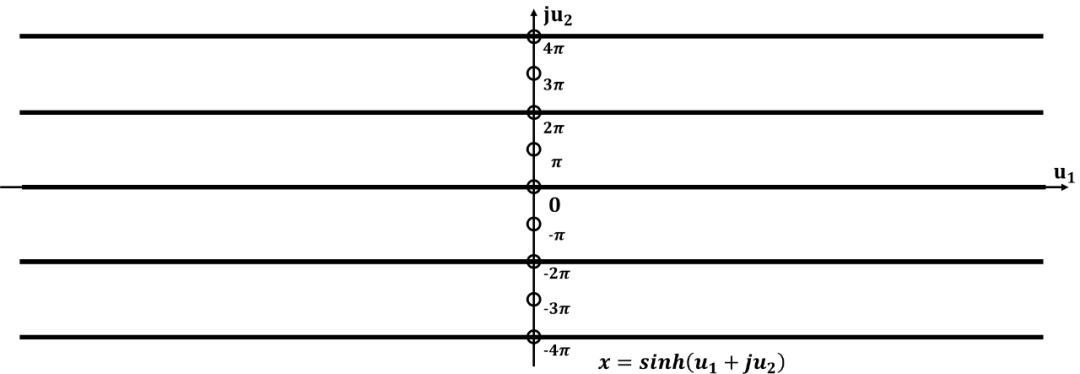
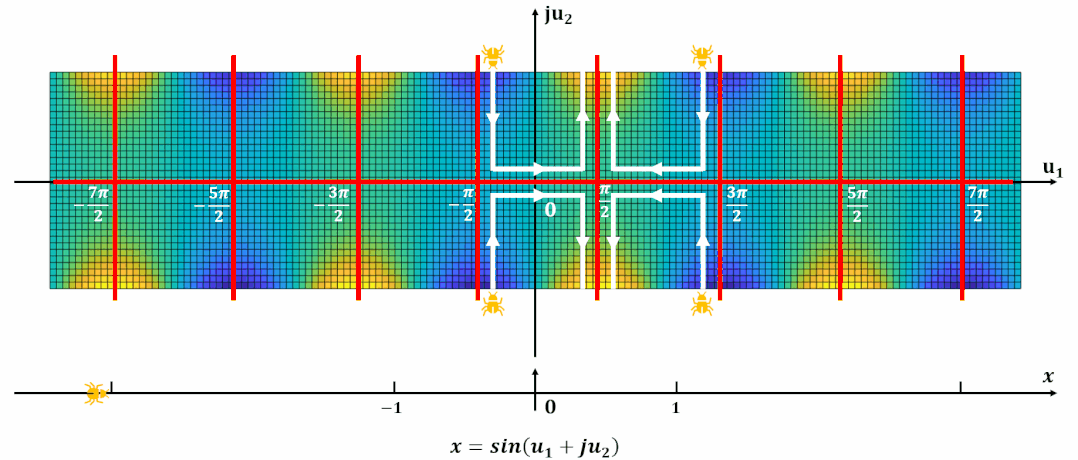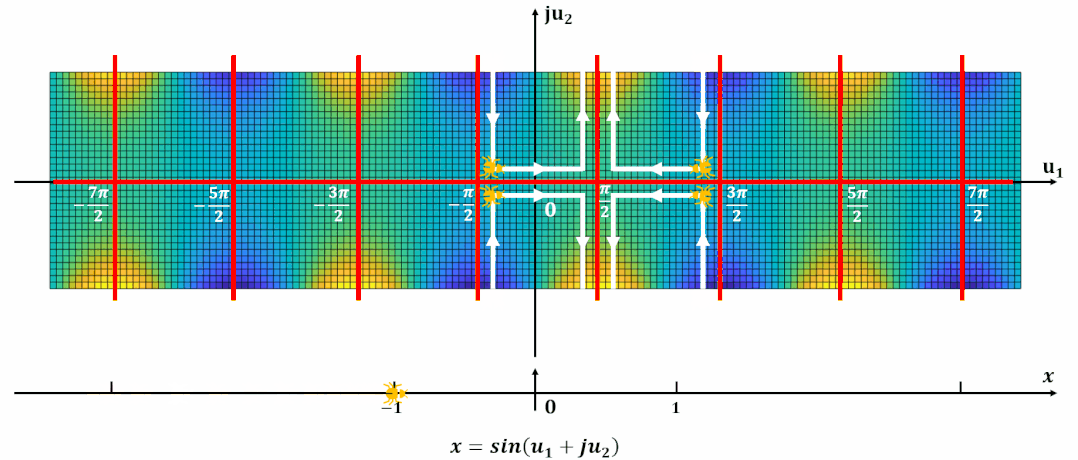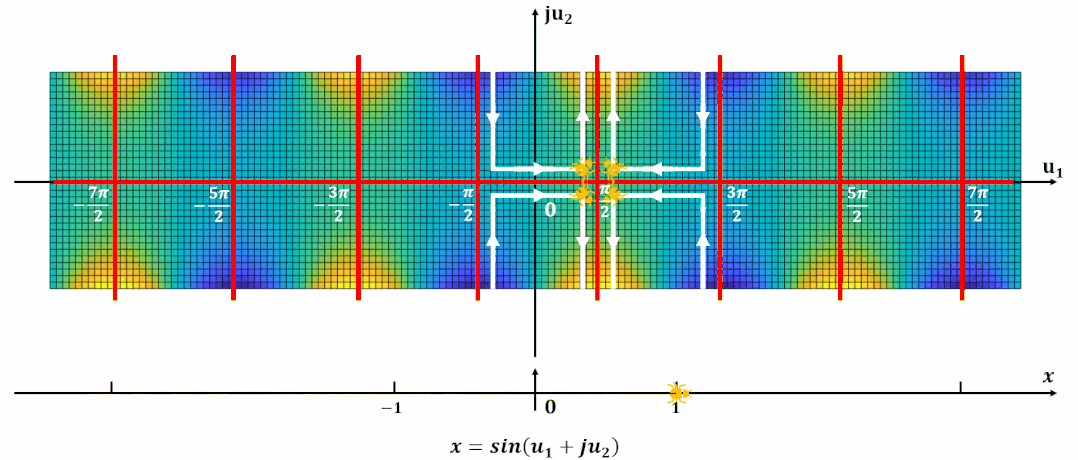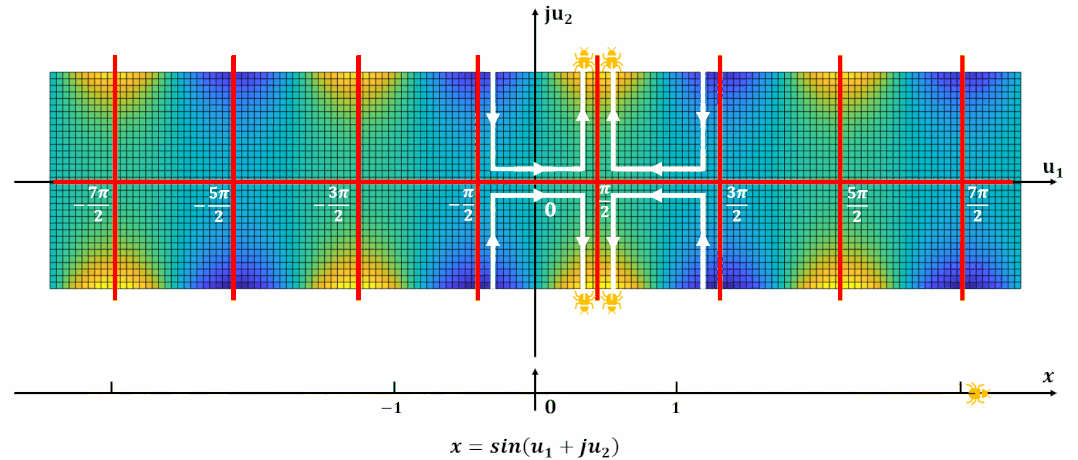
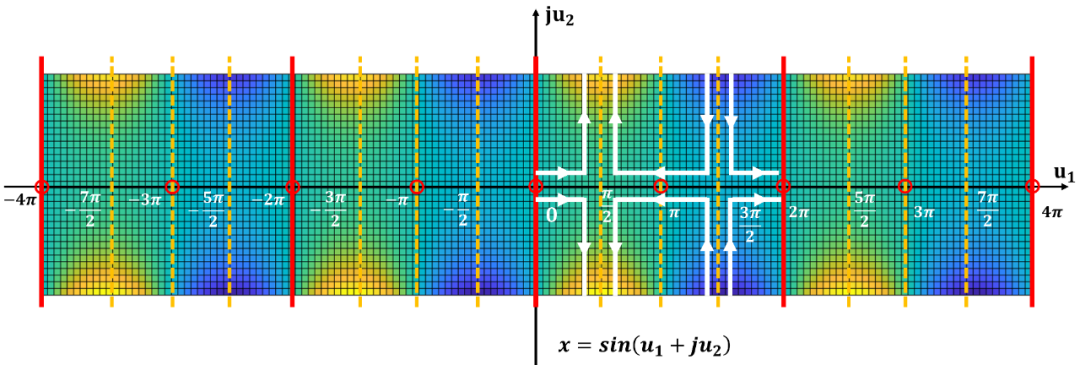
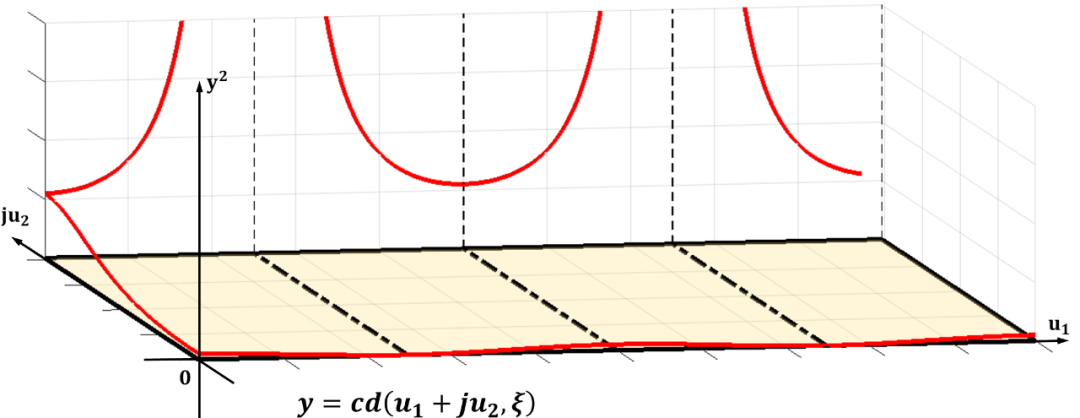
雙周期

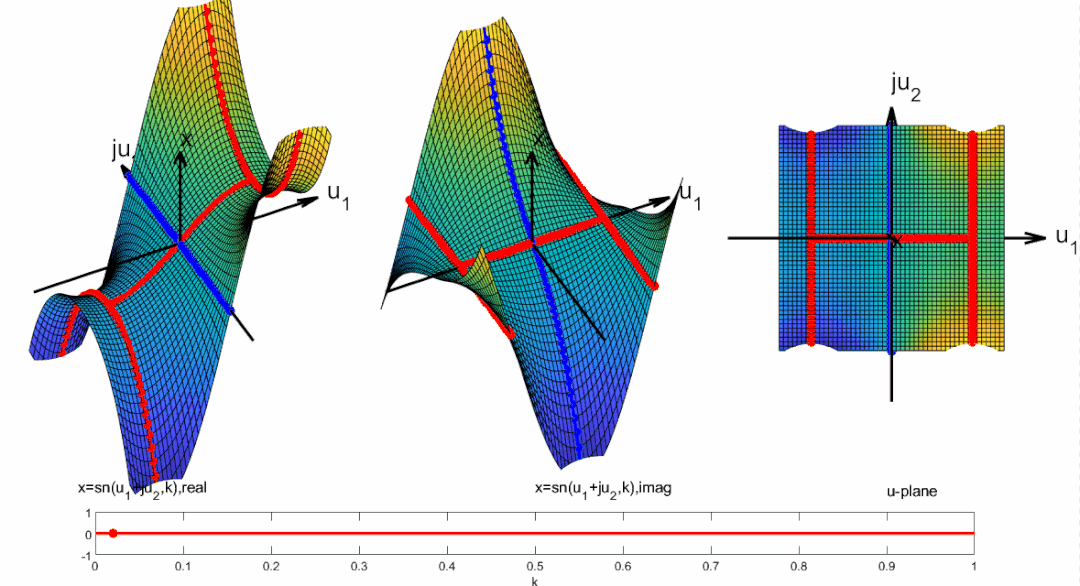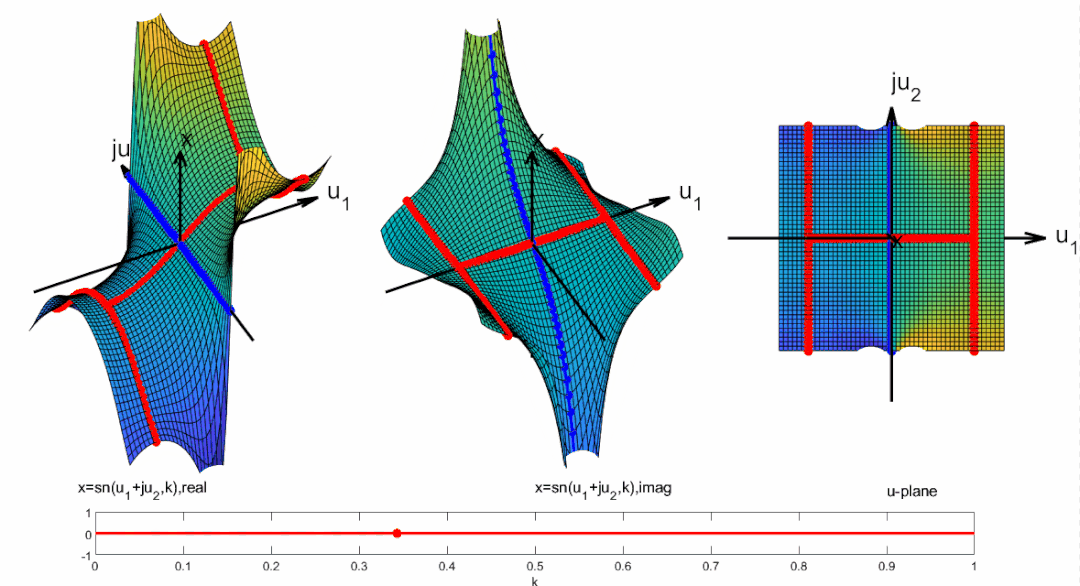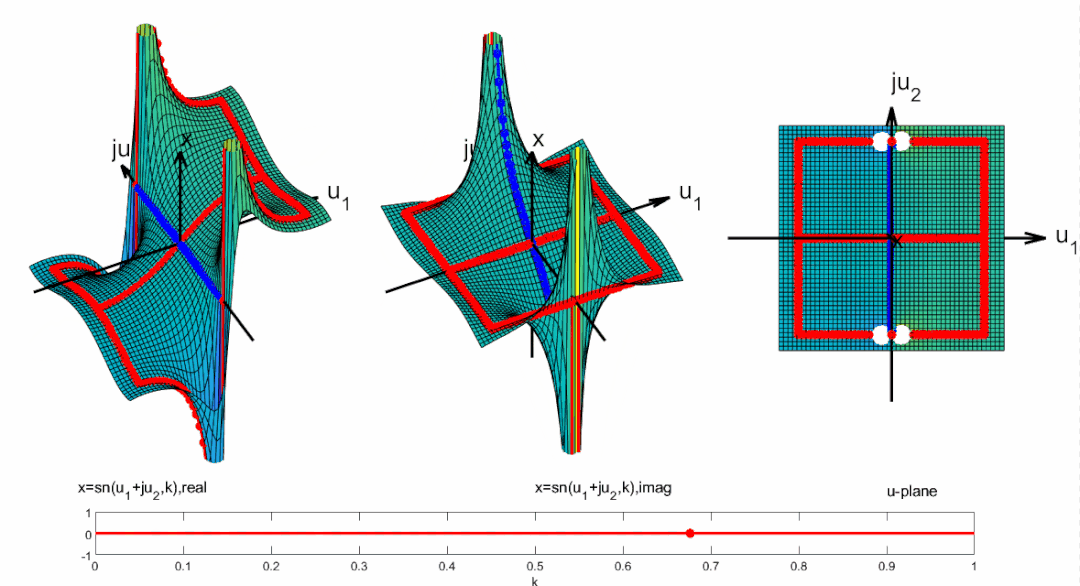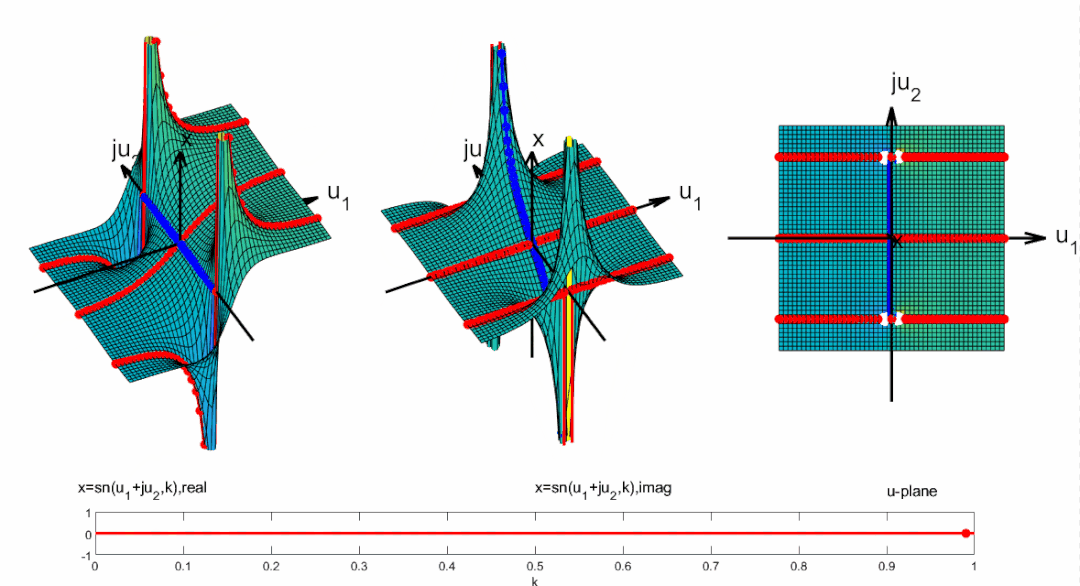
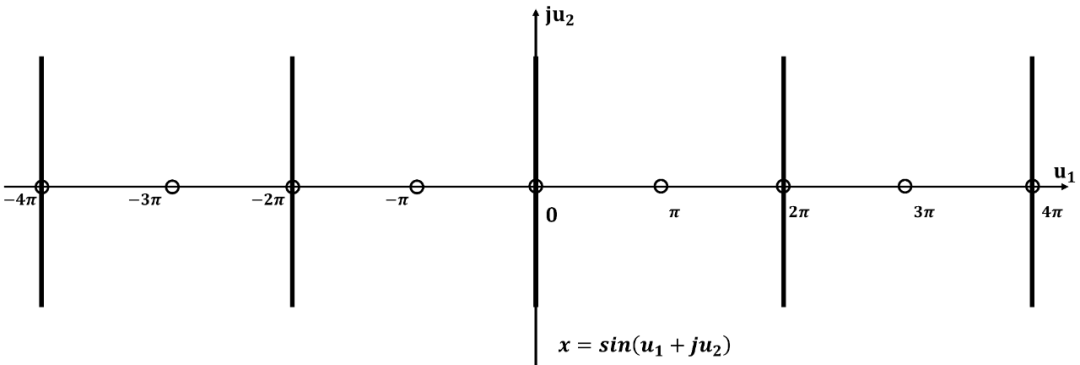
將周期向整個復平面拓展, 并且標出零極點位置:

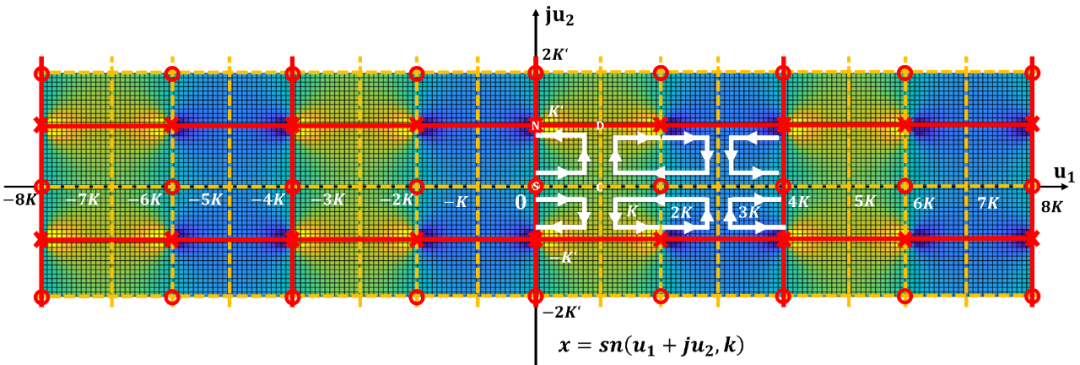
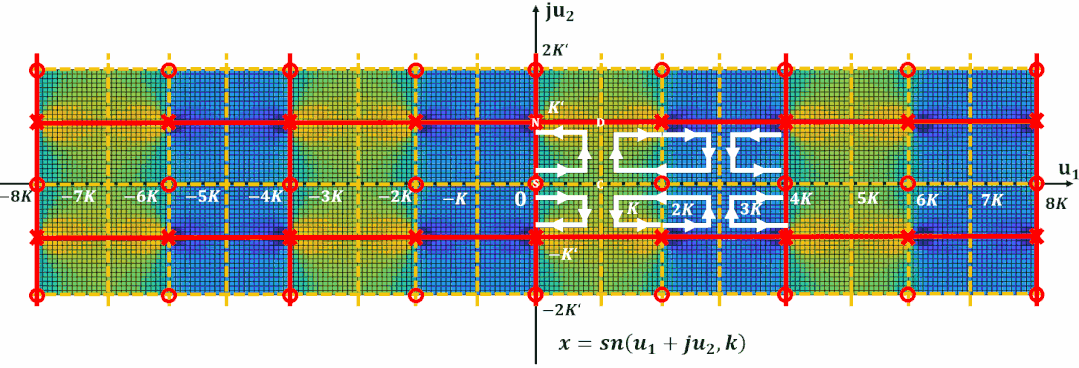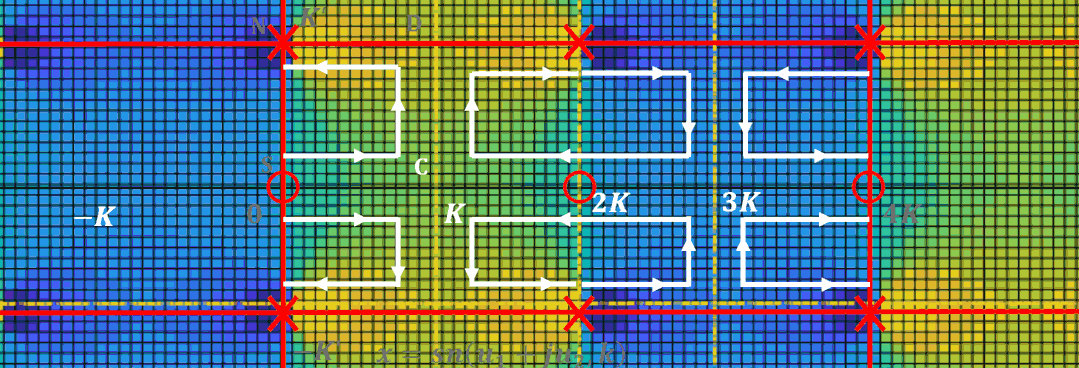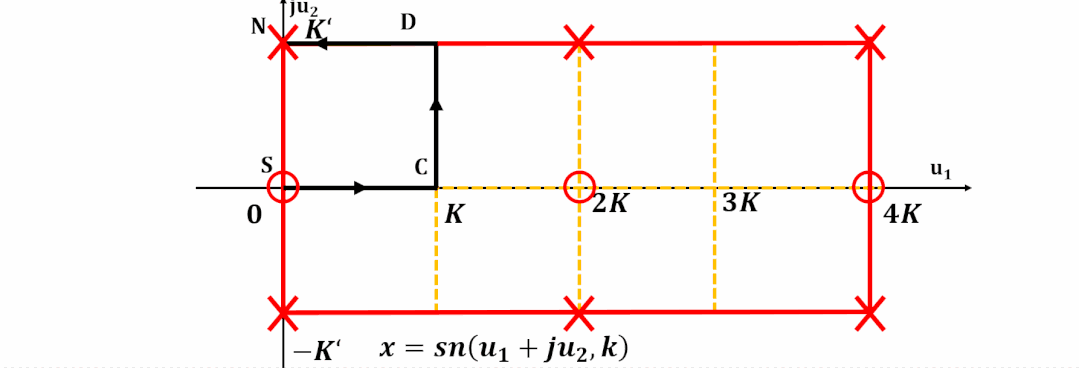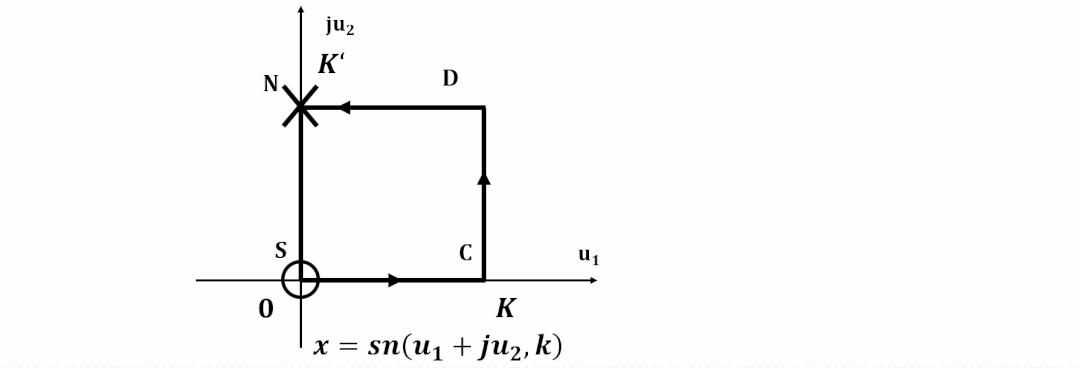
為了更容易對濾波器設計進行計算, 計算機程序都對雅可比橢圓函數進行了歸一化。

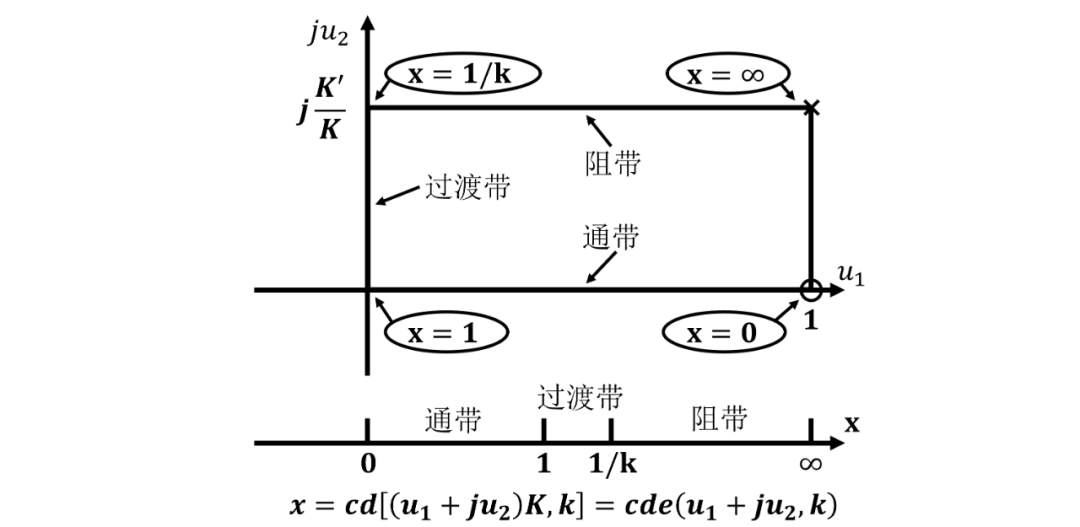
這樣雅可比橢圓函數在-平面實軸上的周期為實數4, 更加方便分析和計算。

橢圓積分和雅可比橢圓函數的數值求解

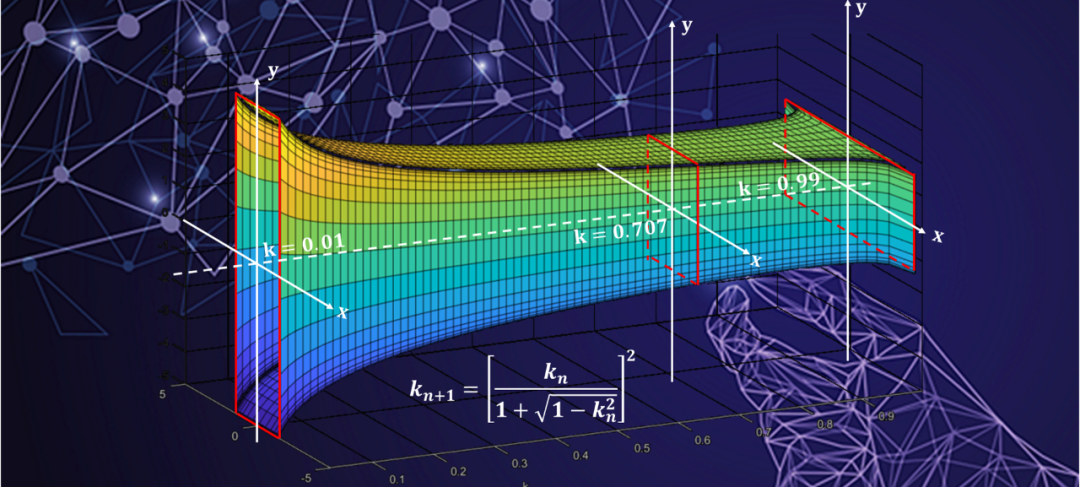
當然橢圓積分的數值計算方法有很多種, 除了蘭登變換外, 還有數值積分和級數展開方法。

橢圓積分的數值計算

蘭登變換(Landen Transformation)的幾何解釋如下:

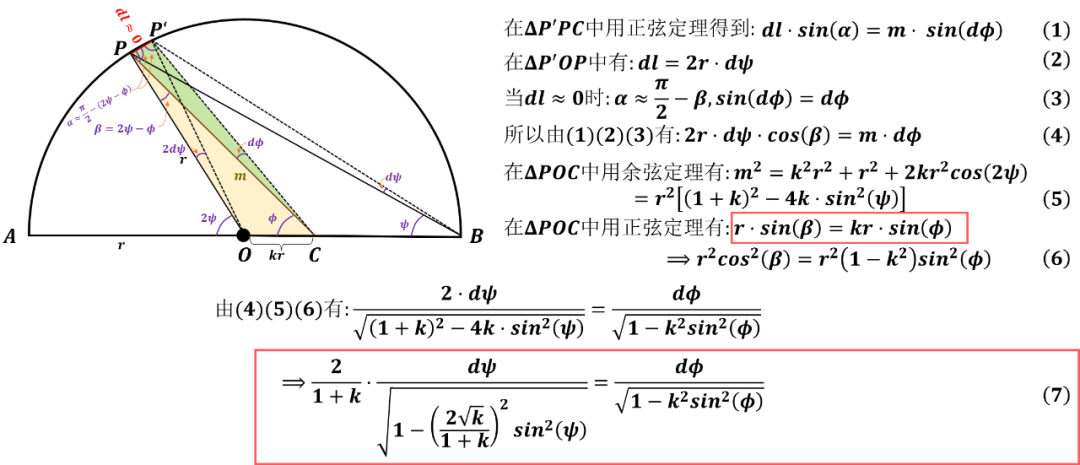
這樣建立了橢圓積分的一般遞推表達式。更多關于蘭登變換的內容見《高斯，蘭登，拉馬努金，算術幾何平均數，橢圓，，和女士日志》。

文獻中提供了3種橢圓積分的數值求解方法:

方法1(模數遞增)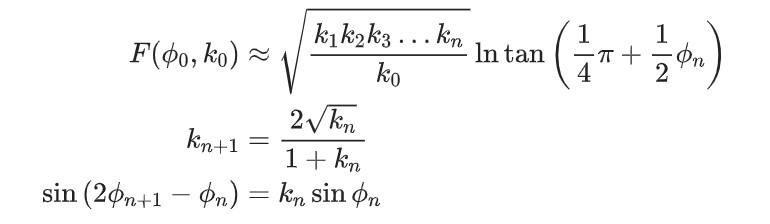

Matlab驗證結果如下:

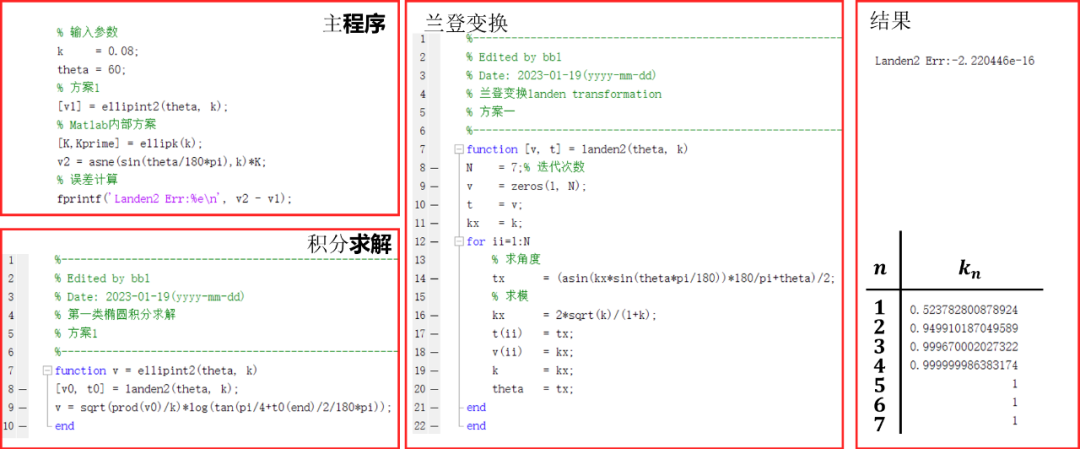
和Matlab原生態函數計算結果相差級別誤差。

方法2(模數遞減)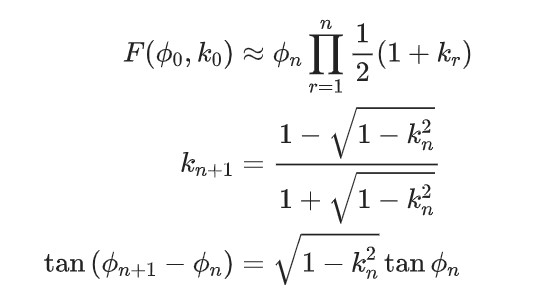

Matlab驗證結果如下:

Matlab驗證結果如下:

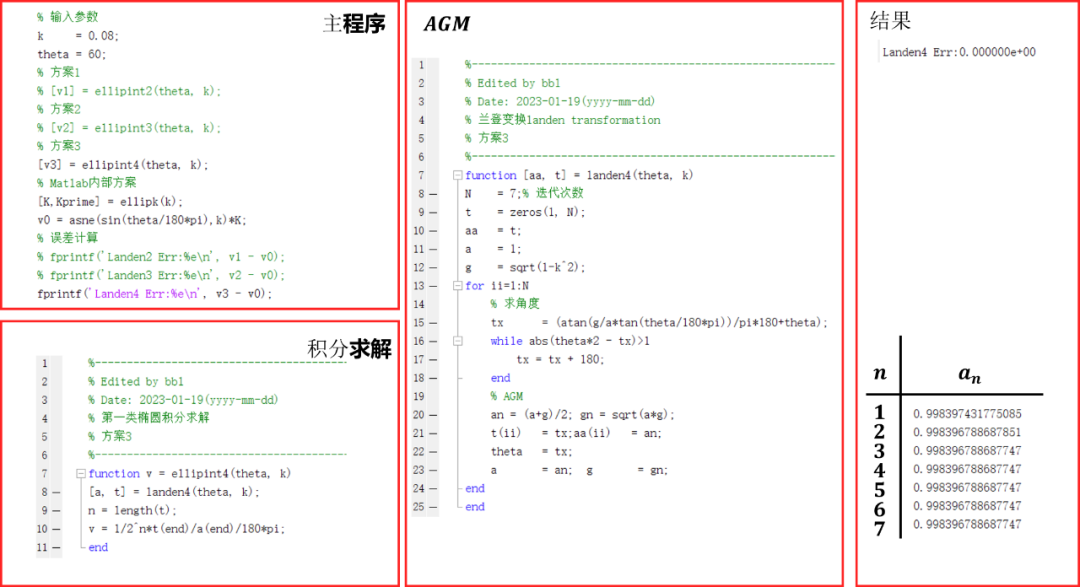
和Matlab原生態函數計算結果完全一樣, 誤差為0。

雅可比橢圓函數數值計算

方案1(AGM)

使用AGM可以對雅可比橢圓函數的數值計算, 也就是前述橢圓積分方案3的逆運算: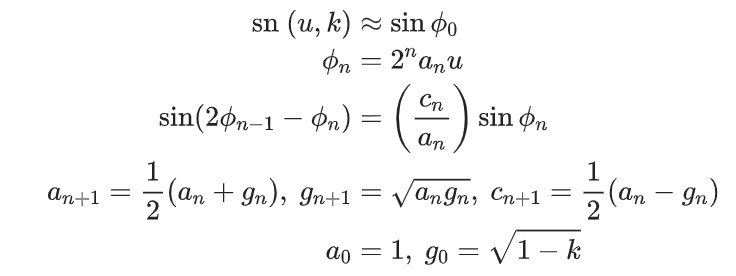

Matlab驗證結果如下:

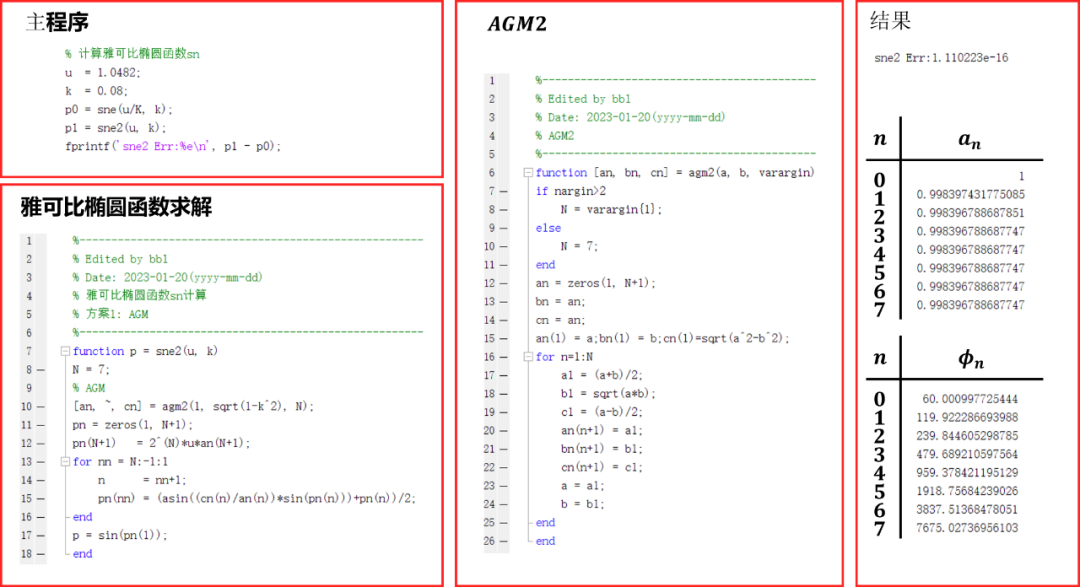
Matlab驗證結果如下:

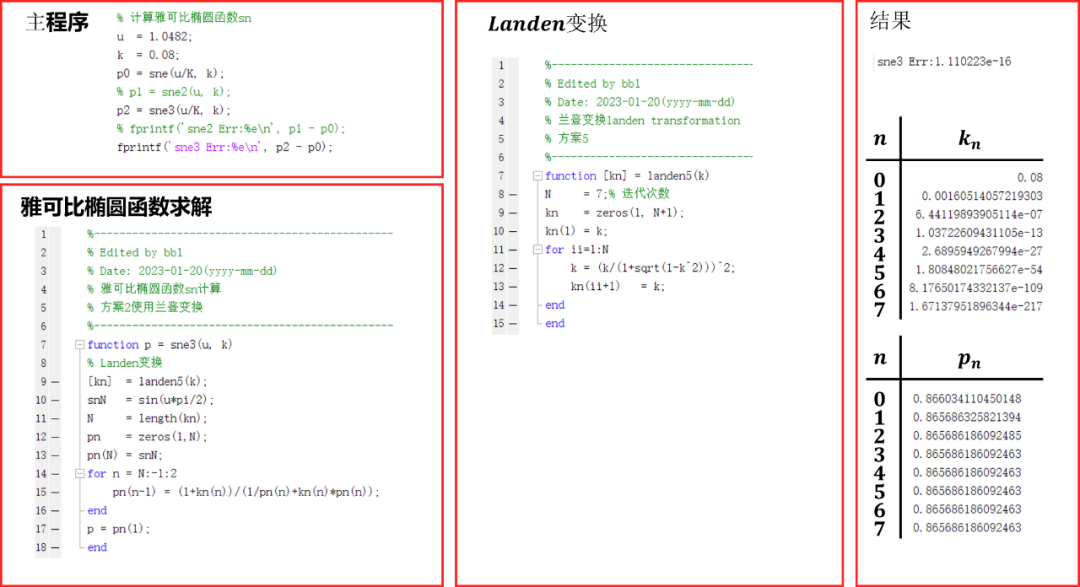
階方程(Degree Equation)

特征方程(The Characteristic Function)

總結

本文主要對《濾波器設計中的橢圓函數》進行進一步分析和講解, 并且建立了微分方程和橢圓濾波器特征方程之間的關系, 為后續講解函數逼近(Approxmation)中的等紋波到微分方程之間建立聯系。

審核編輯：劉清