前言

邊緣檢測是圖像處理和計算機視覺中，尤其是特征提取中的一個研究領域。有許多方法用于邊緣檢測，它們的絕大部分可以劃分為兩類：

基于一階導數

首先計算邊緣強度， 通常用一階導數表示， 例如梯度模，然后，用計算估計邊緣的局部方向， 通常采用梯度的方向，并利用此方向找到局部梯度模的最大值。

即：圖像一階導數中的最大和最小值來檢測邊界，通常是將邊界定位在梯度最大的方向。

一階:Roberts Cross算子，Prewitt算子，Sobel算子， Kirsch算子，羅盤算子；

基于 零穿越/零交叉 的一類：二階導數

基于零穿越的方法通過尋找圖像二階導數零穿越來尋找邊界，通常是Laplacian過零點或者非線性差分表示的過零點。

基于二階導數：Marr-Hildreth，在梯度方向的二階導數過零點，Canny算子，Laplacian算子。

一、邊緣檢測

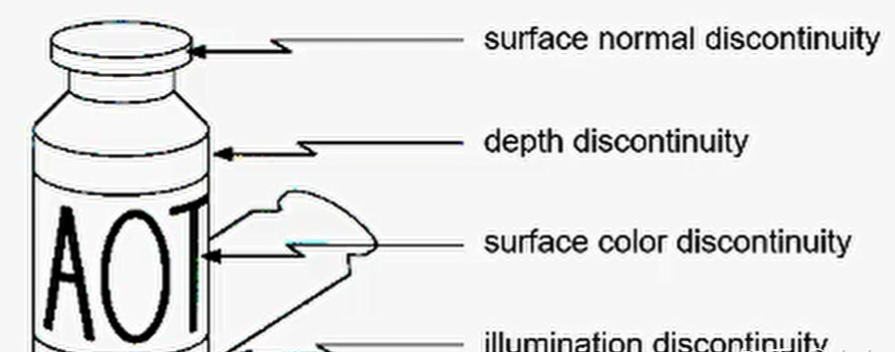
為什么要進行邊緣檢測呢？因為這是穩定的視覺特征，是人類經驗的結果。邊緣檢測的目的是標識數字圖像中亮度變化明顯的點。圖像屬性中的顯著變化通常反映了屬性的重要事件和變化。主要包括：

深度上的不連續（物體處在不同的物平面上）；

表面方向不連續（如正方體的不同的兩個面）

物質屬性變化（會導致光的反射系數不同）

場景照明變化（陰影）

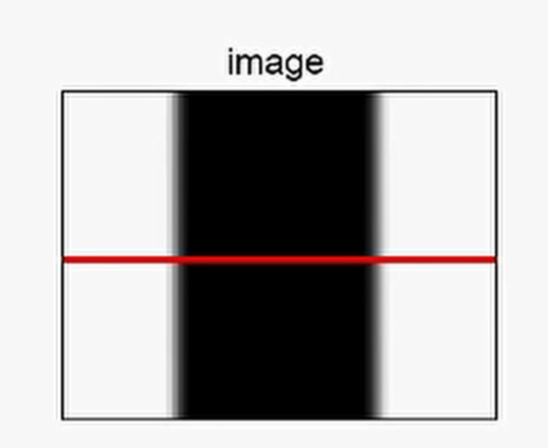
那么，對于下面這張圖像進行邊緣檢測時，沿著這條紅色的水平線，得到其每個像素點上的強度（也就是灰度值），由此可知邊緣就是在像素值發生突變的地方。那么如果從一個信號中找到突變的地方呢？

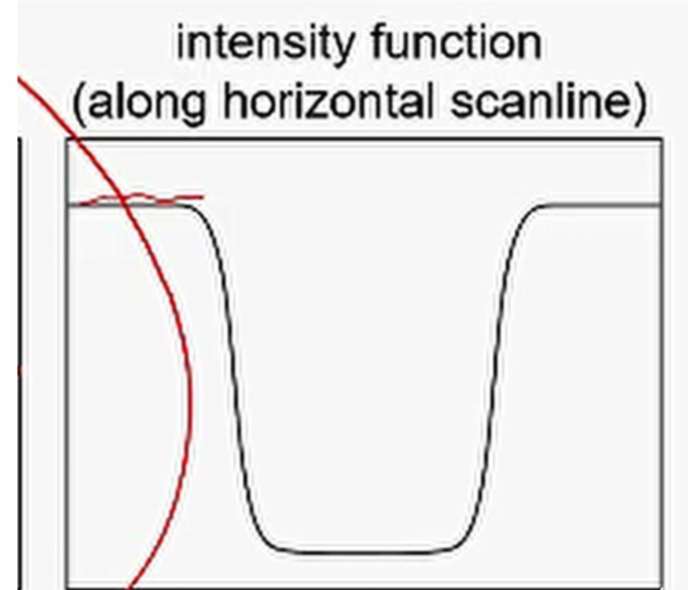
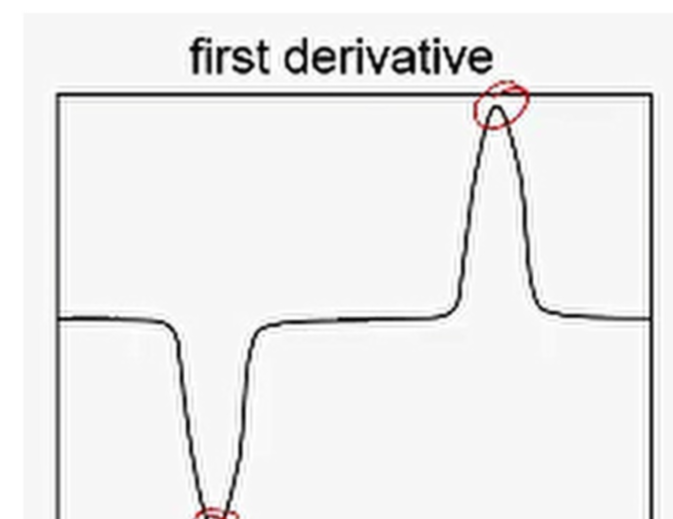
顯然，根據數學知識，對信號曲線進行求一階導數，對于邊緣來說，并不需要關注方向，只需要關注極值即可，所以可以通過求導得到邊緣所在位置。

由此將這跟紅色的水平線從上至下滑動即可得到整個圖像的豎直方向上的邊緣。

對于一個二元函數f（x，y） ，響應的的求導公式：

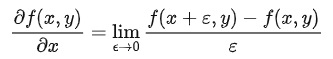
在圖像處理過程中，對于像素值的位置的最小單位是 1 px，因此令 ε=1 ，使用這種近似來作為點前位置的導數，則有：

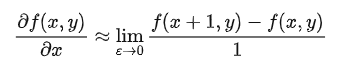
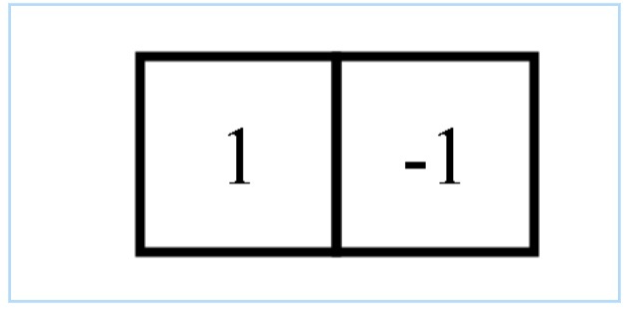
其實由這個公式可以看出，就是右面一個像素減去左面一個像素，作為當前位置的導數，這樣簡化之后其實就可以把這個過程使用卷積代替，即卷積核為：這就是檢測豎直方向上邊緣的卷積核。同理也可以得到水平方向上邊緣的卷積核。

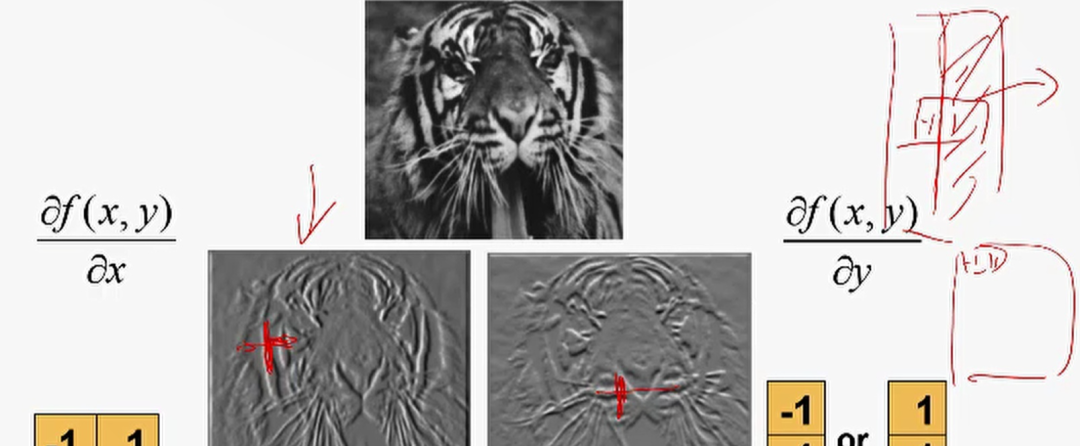
那么接下來舉個例子，下面這兩個邊緣檢測結果哪個是水平方向卷積核檢測到的？

哪個是豎直方向卷積核檢測到的？因為只有水平卷積核檢測的是左右差異較大的像素值，自然而然連成線之后就是豎直方向的線條。

接下來，解釋一下梯度（一維叫導數，高維叫梯度），對于一副圖像的一個像素點

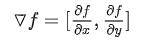
這個幅值越大說面這點附近像素值變化越劇烈，就越有可能是邊緣。

其實梯度對于一副圖像來說就是圖像變化劇烈的方向。而且梯度方向與邊緣是垂直的。

二、邊緣檢測流程

由于在實際應用過程中信號的采集往往伴隨著噪聲的出現，假設有下面這么一個一維信號，很顯然邊緣就在突變的地方。但是由于真實點附近存在噪聲，如果直接使用邊緣濾波器（邊緣卷積）得到的結果會是什么樣？

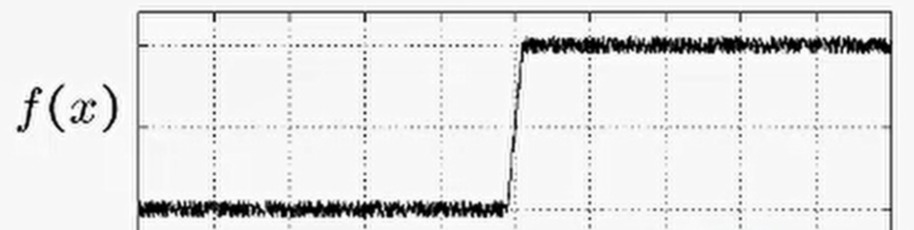
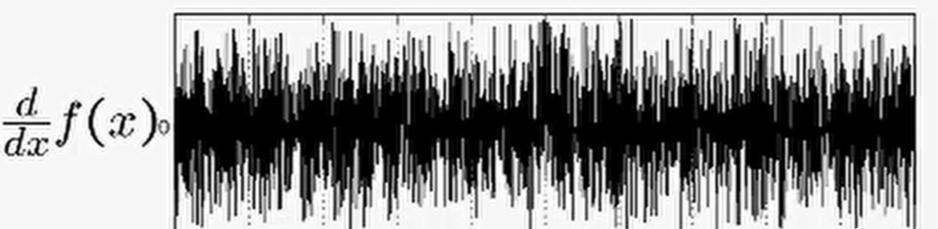
顯然，通過邊緣檢測器之后得到導數（梯度）是無法確定極大值極小值的，因此無法判斷邊緣位置。所以，往往在進行邊緣檢測前首先要進行濾波。

這是因為邊緣檢測算子主要是基于圖像強度的一階導數和二階導數，但是通常情況下導數對噪聲十分敏感，因此必須使用濾波器來進行平滑噪聲。

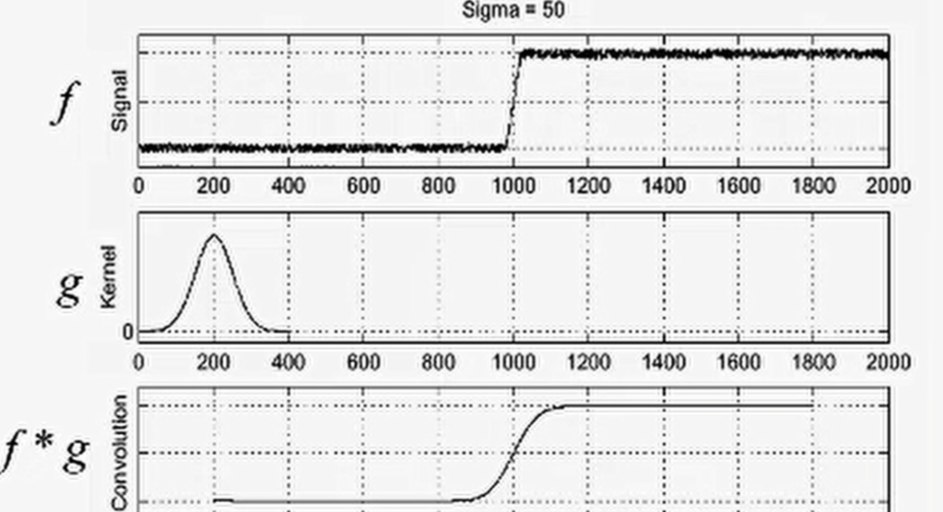
因此對于一維圖像f使用高斯卷積核 g進行濾波，通過將f*g(卷積)得到的結果可以看出，最左邊和最右面為什么沒了呢？這就是因為卷積過程中如果不對邊界補充的話，卷積結果相比原來圖像會小一圈。

經過高斯卷積之后的圖像就相對平滑很多，在這個基礎上再進行邊緣檢測，得到結果如下。很顯然求極值就十分簡單了。

因此，我們在對圖像進行邊緣檢測前首先用高斯卷積對圖像進行平滑就是了，因為我們也無法確定圖像是否包含噪聲。

雖然上面這個過程實現了邊緣檢測，但是在這個過程中使用了兩次卷積，首先是濾波過程的卷積，然后是求導過程的卷積，顯然卷積是十分耗時的，那么能否使用一次卷積完成這個操作呢？

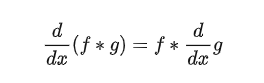
這個公式成立是因此卷積是滿足交換律，結合律和分配率的。所以使用右面的公式，先對高斯卷積核進行求導，這個模板一般比較小，求導也相對簡單，然后再進行卷積。這樣就能加速運算過程了。

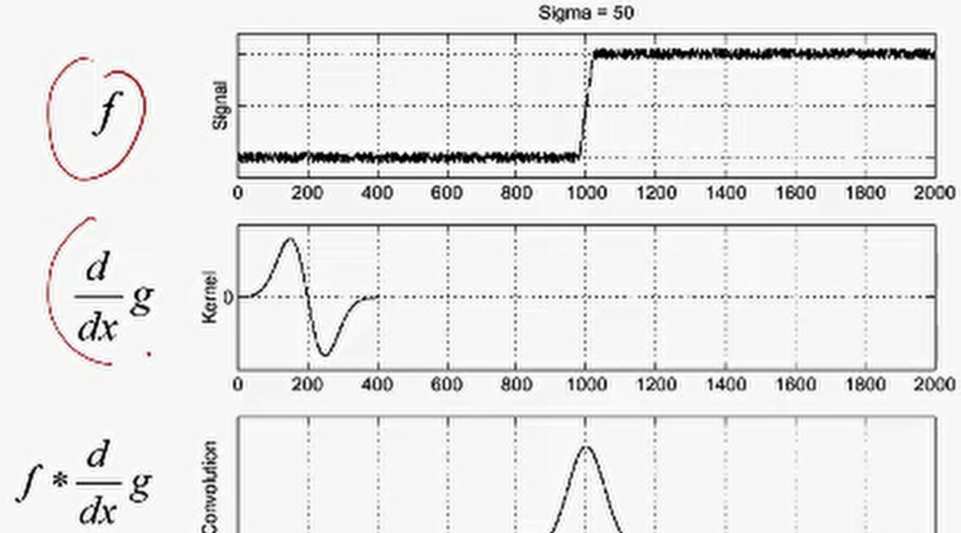
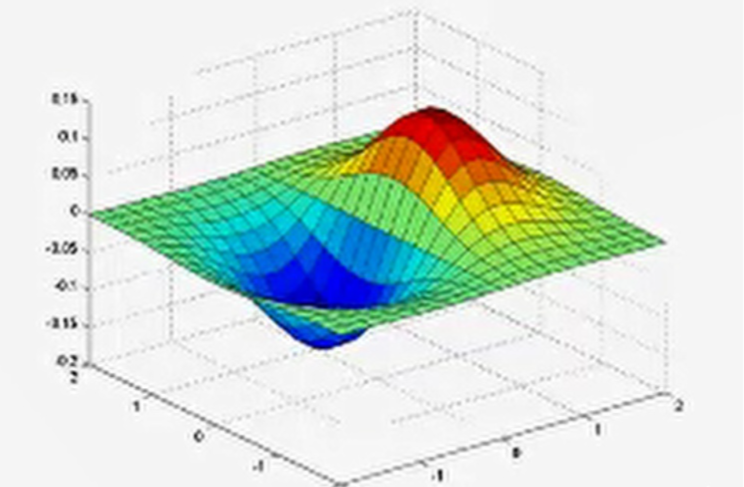
雖然，使用平滑對圖像進行去噪，但是它也會模糊圖像，因此我們可以考慮在不同的scale下進行邊緣檢測。

也就是選擇響應的窗寬和標準差即可對圖像進行平滑并邊緣檢測，由于窗寬一般默認經驗值3σ，因此只需要指定參數σ即可執行這兩個過程。所以可以考慮使用不用的σ在不同的scale下進行邊緣檢測。

因此，接下來對比重新認識一下高斯卷積核與高斯一階導數核的區別：

高斯卷積核（smoothing filters）：高斯卷積實際上是濾除高頻信號，是低通濾波器，濾波器模板中的數值沒有負數，而且這些值相加和為1。

高斯一階導數核（derivative filters）：濾波器模板中的數值一定有負數，而且這些相加為0。

總結一下，對于一副圖像進行邊緣檢測的流程

濾波

增強，增強算法可以將圖像灰度點鄰閾強度值有顯著變化的點凸顯出來。

邊緣檢測，經過增強的圖像，往往鄰域中有很多點的梯度值比較大，而在特定應用中，這些點并不是要找的邊緣點，所以應該采用某些方法對這些點進行取舍。實際工程中，常用的方法是通過閾值化的方法進行檢測。

三、Canny邊緣檢測

對于這樣一張圖像進行邊緣檢測時，首先第一步，對圖像進行濾波處理，然后計算兩個方向的梯度，先計算每個像素點的梯度，然后計算幅值，得到下面這張圖像。

在進行梯度計算時，梯度較大的地方可能是邊緣也有可能是噪聲，雖然已經進行過一次平滑濾波，但是仍然還會有一些高強度的噪聲無法濾除，因此在這里選擇使用閾值對其進行第二次過濾，去除一些梯度相對較小的點。

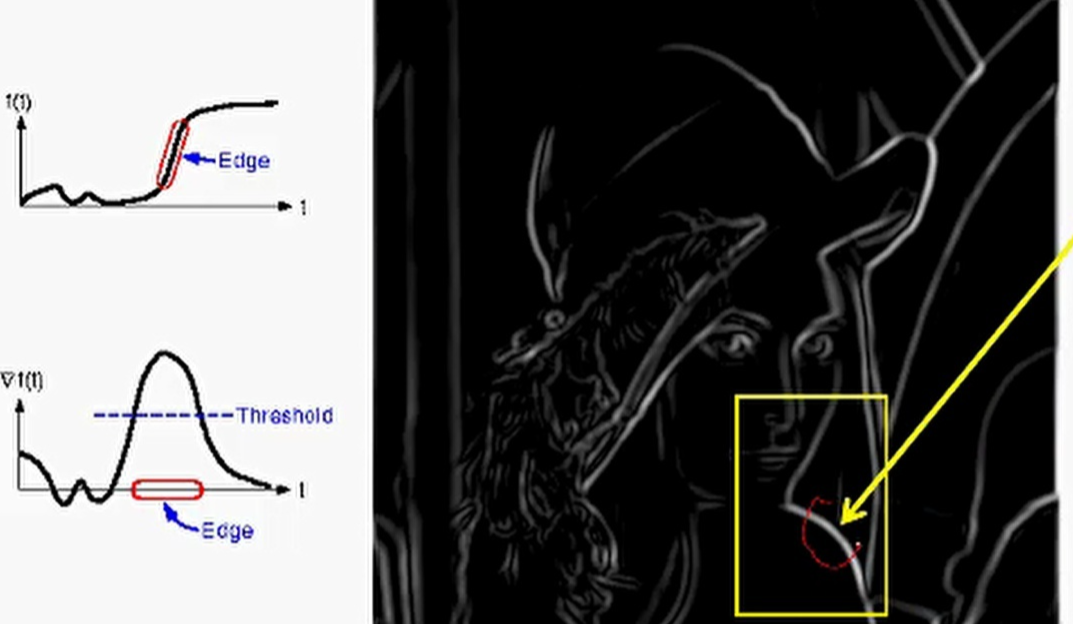
然而經過閾值處理后，還是會有一些小問題，就是圖像中的邊緣會很寬，這是由于圖像中的邊緣像素值都是緩慢變化的，不會是一個垂直的突變，即使原始圖像中的邊緣是一個垂直的突變，經過高斯平滑之后它就會變得不那么垂直了，所以這就是為什么邊會那么寬。那如何解決呢？

接下來就介紹了一個著名的算法：NMS非極大值抑制。它的一個主要思想就是，首先確定邊上的一個點，然后沿著邊的梯度方向比較跟相鄰點的梯度進行比較，也即是右圖中的q和Ρ，γ進行比較。如果 q 最大則保留，如果不是則舍去。

經過抑制以后：顯然這就細化了很多，但是也會存在一定的問題，比如脖子下面的邊緣消失了，出現了斷斷續續的情況，出現這種情況的原因是什么呢？

這是因為設置的閾值太高了，導致這部分梯度被濾除掉了，但是如果閾值設置的較低又會出現很多“假邊”，因此這里需要對剛剛設置閾值過濾這一步進行改進。

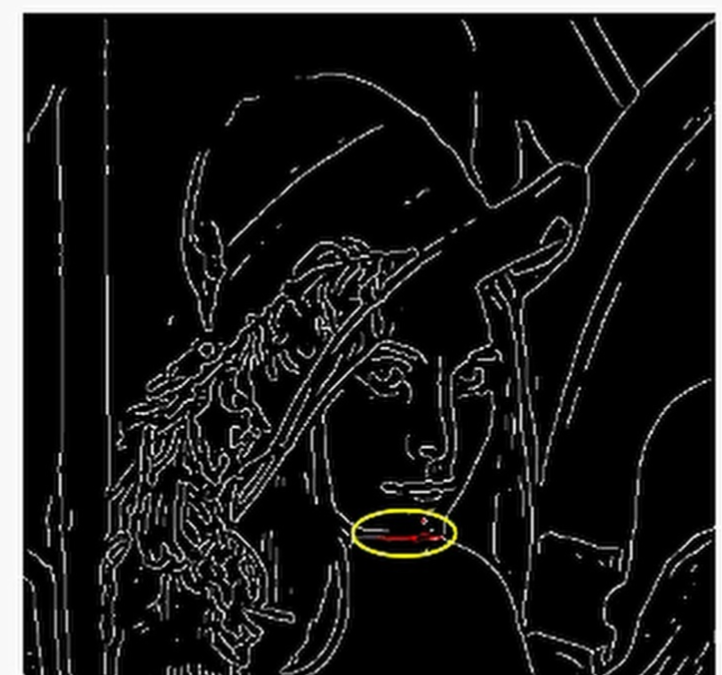
改進的思路：就是使用雙閾值法，首先使用一個較高的閾值去將那些確定度較高的邊檢測出來，稱為“強邊”，然后再使用一個較小的閾值顯露更多的邊，稱為“弱邊”，此時選擇保留那些跟強邊有連接關系的邊。這個想法就很巧妙。

左邊是高閾值，中間是低閾值，右邊是雙閾值

關于Canny邊緣檢測是有嚴格意義上的數學推導的，這個后續補充一下！

審核編輯 ：李倩