使用失配損耗方程,了解失配損耗對射頻功率測量和級聯放大器增益的影響。
有效的功率傳輸是射頻設計中的一個主要問題。由于阻抗不連續性可以反射電波,它們會導致功率損耗,通常稱為失配損耗 (ML),這在各種應用中都有體現。例如,射頻功率傳感器測量的功率,以及射頻模塊級聯的有效增益,都會受到波反射的影響。對于級聯的 RF 塊,我們的目標是盡量減少失配損失,以便我們可以傳輸盡可能多的功率。此外,通過最小化失配損失并為此錯誤開發適當的統計模型,我們可以估計系統中的不確定性。
在本文中,我們將首先研究失配損失方程。然后,我們將討論這種現象對射頻功率測量和級聯放大器有效增益的影響。
失配損失:兩種不同的定義
考慮圖 1 中的圖表,該圖表顯示了在輸入和輸出端口連接到不匹配阻抗(Zs≠ Z0和 ZL≠ Z0 )的傳輸線。
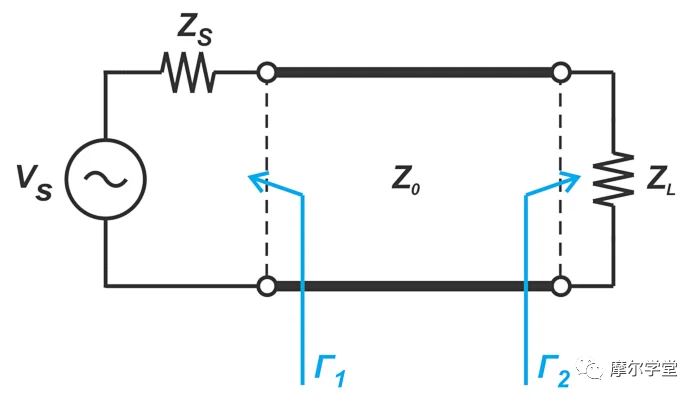
圖 1.示例圖顯示了在輸入和輸出端口連接到不匹配阻抗的傳輸線。
公式 1 顯示了一種定義上述電路失配損耗的方法:
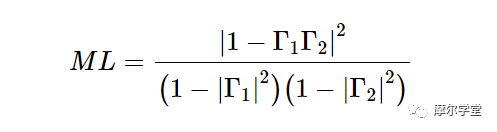
等式 1。
這個等式在之前的文章中進行了非常詳細的研究,它給出了相對于電源可用功率的功率損耗。例如,如果源傳送到共軛匹配負載的功率為 -30 dBW,而實際負載的 ML 為 1 dB,則傳送到負載的功率為 -31 dBW。
根據上述定義,參考功率是可從源獲得的功率。通常使用另一個(實際上更有用的)參考功率來定義失配損耗;源傳送到 Z0終端的功率(其中 Z0是線路的特性阻抗,50 Ω 是標準值)。
考慮到這一點,您可能想知道為什么我們對可以傳輸到 Z0終端的功率感興趣。在 RF 系統中,大多數電路的設計都假設它們將與某些已知的特性阻抗一起使用。換句話說,在正常操作期間,假定大多數電路都具有 Z0源電阻和 Z0負載電阻。這就是為什么 RF 塊通常在這些條件下進行表征的原因。為了更好地理解此功能,請考慮測量雙端口網絡 S 參數的測試設置(圖 2)。
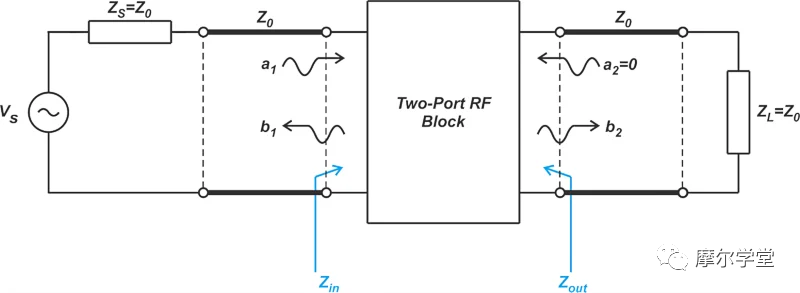
圖 2.為測量雙端口網絡的 S 參數而設置的示例圖。
對于 S 參數測量,一個端口由串聯電阻為 Z 0的源驅動,另一個端口以 Z0負載端接。使用上圖,我們可以測量輸入反射系數 (S11) 和從端口 1 到端口 2 的傳輸系數 (S21)。
請注意,輸出端口的 Z0終端可確保沒有能量從負載反射 (a2= 0),因此,b1和 b2僅作為入射到輸入端的行波的結果產生端口(a1)。還值得一提的是,網絡輸出阻抗 Zout不必等于 Z0。事實上,Zout= Z0很少見。我們只需要有 ZL= Z0來確保 a2= 0。根據定義,S 參數基于使用匹配終端的測試設置。與其他類型的雙端口網絡表示(例如 T 參數)相比,這顯著簡化了 S 參數的測量。
由于 RF 模塊的響應通常在 Z0環境中表征(ZS= ZL= Z0,其中 Z0= 50 Ω 是標準值),因此需要找到與功率相關的失配損耗源傳送到 Z0終端。
匹配負載警告
對于圖 1 中的電路,通用術語“匹配負載”可以指代兩種不同的條件:?大號=?小號*ZL= Z0。第一個條件對應于最大功率傳輸定理,而第二個條件給出了無反射負載。使用術語匹配負載有時會引起混淆。為了更清楚,我們可以使用術語“共軛匹配”來指代?大號=?小號*和術語“Z0匹配”或“無反射匹配”來描述 ZL= Z0。
失配損耗 WRT 功率傳輸到 Z0終端
考慮圖 1 中的圖表,可以看出失配損耗 (ML) 相對于可提供給負載阻抗 Z0的最大功率的計算公式如下:
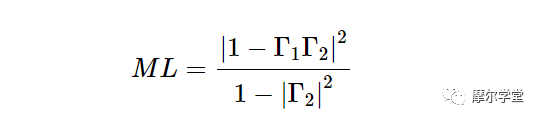
等式 2。
請注意,Γ1和Γ2分別表示線路源端和負載端的反射系數。ML 如公式 2 所示定義,傳輸到 Z 0終端的功率(PZ0) 和傳輸到任意負載的功率 (PLoad) 與以下公式相關:
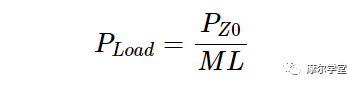
等式 3。
我們也可以用分貝表示上述等式。在許多應用中,Γ 1和Γ2的相位角是未知的;并且我們只能找到 ML 的上限和下限來確定功率傳輸不確定性的范圍。ML 的最大值和最小值之間的差異,稱為失配不確定性 (MU),由下式給出:
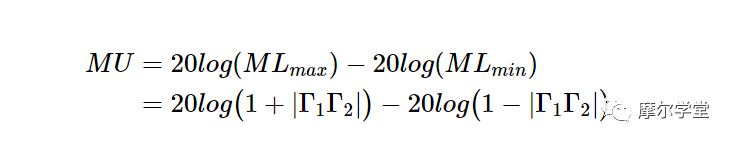
等式 4。
在上一篇文章中,我們使用方程式 1 而不是方程式 2 推導出了相同的方程式。雖然方程式 1 和 2 給出了關于兩個不同參考功率的功率損耗,但正如預期的那樣,它們會導致相同的失配不確定性項。讓我們看一個示例,了解如何在功率傳感器應用中使用上述方程式。
示例 1:RF 功率傳感器
顧名思義,功率傳感器用于測量射頻和微波信號的功率(圖 3)。

圖 3.連接到脈沖功率傳感器的 R&S NRX 功率計。圖片由羅德與施瓦茨提供
理想情況下,傳感器應測量傳送到傳感器的凈功率。實際情況并非如此,因為一些凈輸入功率可能不會在傳感元件中耗散。例如,輻射造成的損失可能會引導能量遠離傳感元件。因此,最終由傳感器 P m測量和指示的功率與傳遞給傳感器的凈功率 PLoad并不完全相同。測試設備制造商使用一些校準系數來描述這兩個量之間的關系:
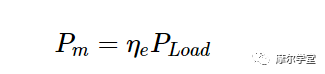
等式 5。
在上式中,ηe稱為“有效效率”。在表征發電機時,所需量通常是 Z 0負載中耗散的功率,而不是功率傳感器輸入阻抗中耗散的功率。將方程式 2 和 3 代入方程式 4 可得出 P Z0的方程式:
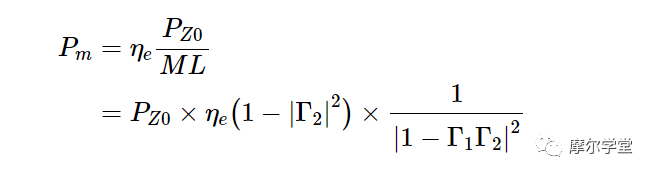
等式 6。
因子 (eta _e ig (1-|Gamma_2|^2)) 稱為校準因子 Kb。大多數現代功率計都能夠消除校準因數中的誤差。使用此功能時,公式 5 可改寫為:??(1?|Γ2|2)稱為校準系數 K
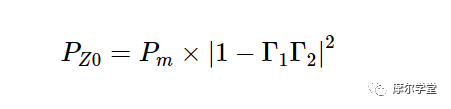
請注意,誤差項實際上與上面討論的失配不確定性 (MU) 有關。例如,如果 (| Gamma_1 |) ≤ 0.09 且 (| Gamma_2 |) ≤ 0.2,則誤差的最大值和最小值是:
|Γ1|≤ 0.09 和|Γ2|≤ 0.2,誤差的最大值和最小值分別為:
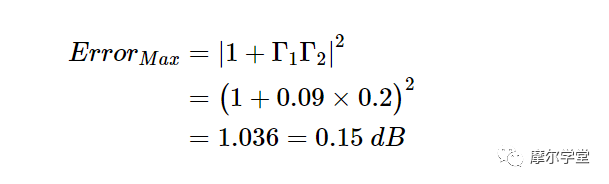
和
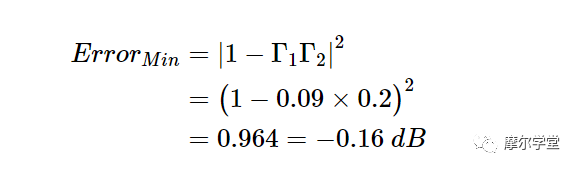
因此,P Z0的實際值可比功率計指示值高0.15 dB或低0.16 dB。
示例 2:級聯塊的有效增益
考慮圖 4 中所示的配置。
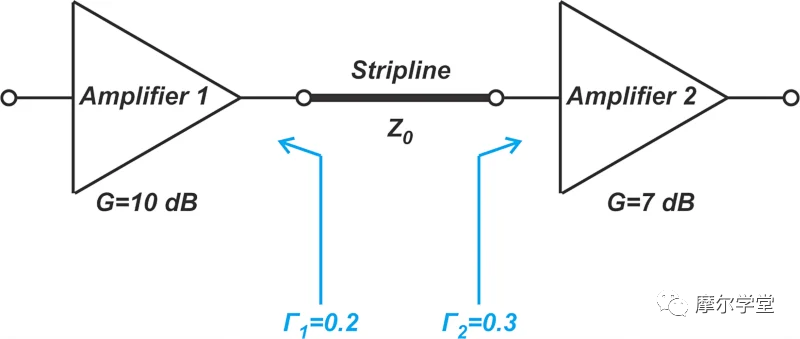
圖 4.通過帶狀線連接的放大器配置示例。
在本例中,放大器 1 和 2 的傳感器增益分別為 10 dB 和 7 dB。由于帶狀線兩端的阻抗不匹配,放大器1提供的部分能量在兩個阻抗不連續點之間來回反彈。可以證明,這些波反射導致功率損耗,由下式給出:
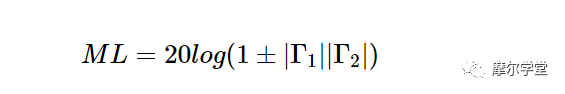
等式 7。
您可以在WF Egan 的《實用射頻系統設計》第 2 章中找到該等式的證明。例如,如果 (| Gamma_1 |) ≤ 0.2 且 (| Gamma_2 |) ≤ 0.3,則失配引起的損耗的最大值和最小值分別為 0.51 dB 和 -0.54 dB。0.54 dB 的負損耗實際上代表額外的功率增益。現在我們可以找到級聯的有效增益。通常,我們期望上述電路的增益為10+7 = 17 dB;然而,由于失配損耗,實際增益可能在 17 - 0.51 = 16.49 dB 和 17 + 0.54 = 17.54 dB 之間變化。|Γ1|≤ 0.2 和|Γ2|≤ 0.3,失配引起的損耗的最大值和最小值分別為 0.51 dB 和 -0.54 dB。0.54 dB 的負損耗實際上代表額外的功率增益。現在我們可以找到級聯的有效增益。通常,我們期望上述電路的增益為10+7 = 17 dB;然而,由于失配損耗,實際增益可能在 17 - 0.51 = 16.49 dB 和 17 + 0.54 = 17.54 dB 之間變化。
射頻功率傳輸設計中的失配損耗和阻抗
阻抗不連續性使我們無法在 RF 設計中進行有效的功率傳輸。這表現為功率損耗,并導致各種應用中的不確定性。在本文中,我們討論了射頻功率傳感器測量的功率和級聯放大器的有效增益受失配損耗的影響。
審核編輯:陳陳
-
放大器
+關注
關注
143文章
13619瀏覽量
213849 -
增益
+關注
關注
3文章
377瀏覽量
36812 -
射頻功率
+關注
關注
0文章
40瀏覽量
12942
原文標題:失配損耗對射頻功率測量和級聯放大器增益的影響
文章出處:【微信號:moorexuetang,微信公眾號:摩爾學堂】歡迎添加關注!文章轉載請注明出處。
發布評論請先 登錄
相關推薦




 失配損耗對射頻功率測量和級聯放大器增益的影響是什么
失配損耗對射頻功率測量和級聯放大器增益的影響是什么












評論