6、DBSCAN

DBSCAN 聚類（其中 DBSCAN 是基于密度的空間聚類的噪聲應用程序）涉及在域中尋找高密度區域，并將其周圍的特征空間區域擴展為群集。

…我們提出了新的聚類算法 DBSCAN 依賴于基于密度的概念的集群設計，以發現任意形狀的集群。DBSCAN 只需要一個輸入參數，并支持用戶為其確定適當的值

-源自：《基于密度的噪聲大空間數據庫聚類發現算法》，1996

它是通過 DBSCAN 類實現的，主要配置是“ eps ”和“ min _ samples ”超參數。

下面列出了完整的示例。

# dbscan 聚類
from numpy import unique
from numpy import where
from sklearn.datasets import make_classification
from sklearn.cluster import DBSCAN
from matplotlib import pyplot
# 定義數據集
X, _ = make_classification(n_samples=1000, 
                           n_features=2, 
                           n_informative=2, 
                           n_redundant=0, 
                           n_clusters_per_class=1, 
                           random_state=4)
# 定義模型
model = DBSCAN(eps=0.30, min_samples=9)
# 模型擬合與聚類預測
yhat = model.fit_predict(X)
# 檢索唯一群集
clusters = unique(yhat)
# 為每個群集的樣本創建散點圖
for cluster in clusters:
    # 獲取此群集的示例的行索引
    row_ix = where(yhat == cluster)
    # 創建這些樣本的散布
    pyplot.scatter(X[row_ix, 0], X[row_ix, 1])
# 繪制散點圖
pyplot.show()

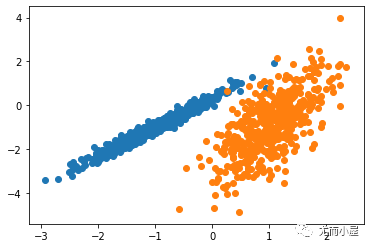
運行該示例符合訓練數據集上的模型，并預測數據集中每個示例的群集。然后創建一個散點圖，并由其指定的群集著色。在這種情況下，盡管需要更多的調整，但是找到了合理的分組。

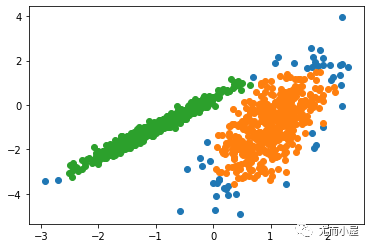
圖：使用DBSCAN集群識別出具有集群的數據集的散點圖

7、K均值

K-均值聚類可以是最常見的聚類算法，并涉及向群集分配示例，以盡量減少每個群集內的方差。

本文的主要目的是描述一種基于樣本將 N 維種群劃分為 k 個集合的過程。這個叫做“ K-均值”的過程似乎給出了在類內方差意義上相當有效的分區。

-源自：《關于多元觀測的分類和分析的一些方法》1967年

它是通過 K-均值類實現的，要優化的主要配置是“ n _ clusters ”超參數設置為數據中估計的群集數量。下面列出了完整的示例。

# k-means 聚類
from numpy import unique
from numpy import where
from sklearn.datasets import make_classification
from sklearn.cluster import KMeans
from matplotlib import pyplot
# 定義數據集
X, _ = make_classification(n_samples=1000, 
                           n_features=2, 
                           n_informative=2,
                           n_redundant=0,
                           n_clusters_per_class=1, 
                           random_state=4)
# 定義模型
model = KMeans(n_clusters=2)
# 模型擬合
model.fit(X)
# 為每個示例分配一個集群
yhat = model.predict(X)
# 檢索唯一群集
clusters = unique(yhat)
# 為每個群集的樣本創建散點圖
for cluster in clusters:
    # 獲取此群集的示例的行索引
    row_ix = where(yhat == cluster)
    # 創建這些樣本的散布
    pyplot.scatter(X[row_ix, 0], X[row_ix, 1])
# 繪制散點圖
pyplot.show()

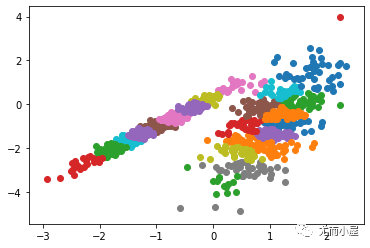
運行該示例符合訓練數據集上的模型，并預測數據集中每個示例的群集。然后創建一個散點圖，并由其指定的群集著色。在這種情況下，可以找到一個合理的分組，盡管每個維度中的不等等方差使得該方法不太適合該數據集。

圖：使用K均值聚類識別出具有聚類的數據集的散點圖

8、Mini-Batch K-均值

Mini-Batch K-均值是 K-均值的修改版本，它使用小批量的樣本而不是整個數據集對群集質心進行更新，這可以使大數據集的更新速度更快，并且可能對統計噪聲更健壯。

...我們建議使用 k-均值聚類的迷你批量優化。與經典批處理算法相比，這降低了計算成本的數量級，同時提供了比在線隨機梯度下降更好的解決方案。

—源自：《Web-Scale K-均值聚類》2010

它是通過 MiniBatchKMeans 類實現的，要優化的主配置是“ n _ clusters ”超參數，設置為數據中估計的群集數量。下面列出了完整的示例。

# mini-batch k均值聚類
from numpy import unique
from numpy import where
from sklearn.datasets import make_classification
from sklearn.cluster import MiniBatchKMeans
from matplotlib import pyplot
# 定義數據集
X, _ = make_classification(n_samples=1000, 
                           n_features=2, 
                           n_informative=2, 
                           n_redundant=0,
                           n_clusters_per_class=1,
                           random_state=4)
# 定義模型
model = MiniBatchKMeans(n_clusters=2)
# 模型擬合
model.fit(X)
# 為每個示例分配一個集群
yhat = model.predict(X)
# 檢索唯一群集
clusters = unique(yhat)
# 為每個群集的樣本創建散點圖
for cluster in clusters:
    # 獲取此群集的示例的行索引
    row_ix = where(yhat == cluster)
    # 創建這些樣本的散布
    pyplot.scatter(X[row_ix, 0], X[row_ix, 1])
# 繪制散點圖
pyplot.show()

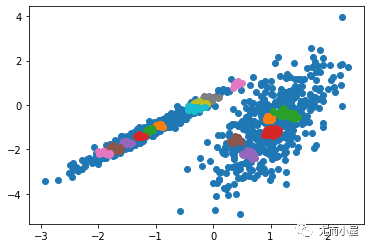
運行該示例符合訓練數據集上的模型，并預測數據集中每個示例的群集。然后創建一個散點圖，并由其指定的群集著色。在這種情況下，會找到與標準 K-均值算法相當的結果。

圖：帶有最小批次K均值聚類的聚類數據集的散點圖

9、均值漂移聚類

均值漂移聚類涉及到根據特征空間中的實例密度來尋找和調整質心。

對離散數據證明了遞推平均移位程序收斂到最接近駐點的基礎密度函數，從而證明了它在檢測密度模式中的應用。

—源自：《Mean Shift ：面向特征空間分析的穩健方法》，2002

它是通過 MeanShift 類實現的，主要配置是“帶寬”超參數。下面列出了完整的示例。

# 均值漂移聚類
from numpy import unique
from numpy import where
from sklearn.datasets import make_classification
from sklearn.cluster import MeanShift
from matplotlib import pyplot
# 定義數據集
X, _ = make_classification(n_samples=1000,
                           n_features=2, 
                           n_informative=2, 
                           n_redundant=0, 
                           n_clusters_per_class=1,
                           random_state=4)
# 定義模型
model = MeanShift()
# 模型擬合與聚類預測
yhat = model.fit_predict(X)
# 檢索唯一群集
clusters = unique(yhat)
# 為每個群集的樣本創建散點圖
for cluster in clusters:
    # 獲取此群集的示例的行索引
    row_ix = where(yhat == cluster)
    # 創建這些樣本的散布
    pyplot.scatter(X[row_ix, 0], X[row_ix, 1])
# 繪制散點圖
pyplot.show()

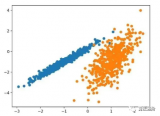
運行該示例符合訓練數據集上的模型，并預測數據集中每個示例的群集。然后創建一個散點圖，并由其指定的群集著色。在這種情況下，可以在數據中找到一組合理的群集。

圖：具有均值漂移聚類的聚類數據集散點圖