這篇文章來源于DevicePlus.com英語網站的翻譯稿。
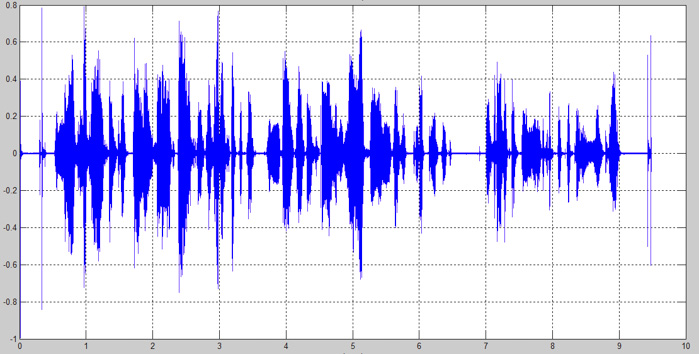
在本教程中,我們將分析語音信號。我們人類發出的聲波是連續的模擬信號,然而對于信號處理,我們需要一個非連續時間模型——計算機的數字模型。本文的主要目的是幫助大家了解如何實現數字信號處理。我們將會比較自己錄制的聲音和一個失真信號,從中尋找2個語音信號之間的相似點和不同點。
對于這個項目,有一點比較重要:我們應該在應用不同的參數時,著重了解波形模式以及它們如何隨時間變化。在本文(第1部分)中,我們將探討語音信號的一些特性以及如何使用MATLAB處理這種信號;然后,我們使用Arduino對錄制的語音信號進行詳細分析。
軟件
Audacity
Matlab
Arduino IDE
第1步:關于語音信號
處理語音信號時,我們要了解“信號”的含義,這一點很重要。那信號是什么?
通信信號處理 ,作者Paolo Prandoni與Martin Vetterli:
“信號”是對隨時間或空間演變的現象的一種形式描述;通過信號處理,我們可以描述任何手動或“機械”操作,從而修改、分析或操控一個信號中包含的信息。我們舉個環境溫度的簡單例子:我們就這個物理變量的正式模型達成一致——比如攝氏度——之后,我們可以用各種方式記錄溫度隨時間的變化,而結果數據集就代表一個溫度“信號”。
第一步,我們將了解語音信號的屬性。錄制自己的聲音之前,讓我們首先在Audacity中了解一些不同的參數。
聲道數量:
單聲道:您使用一個聲道進行錄音,這意味著只有一個音頻信號——錄音分布在同一音量級別。因此如果您有兩個或更多揚聲器,您聽不出差異。這是最常用的方法,因為聲音是用一個麥克風錄制的,這意味著單聲道占用的帶寬較少,因此對許多應用(比如電話和無線電)來說非常有用。對于不太熟悉音頻設備放置技術細節的用戶來說,單聲道是正確的選擇。
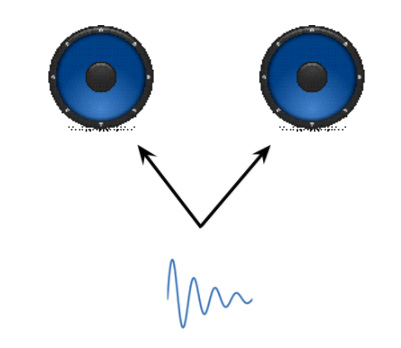
圖1:單個音頻信號在同一音量級別上分配給多個揚聲器(單聲道)
立體聲:您用兩個或更多聲道錄音。由于信號來自多個信號源,因此能夠描述聲音的方向和位置。使用立體聲設置意味著您需要將至少2個麥克風放置在適當的位置。通過這種方式,您可以確定多個聲源的不同位置。這種錄制通常用于電影和音樂,以獲得更廣泛的聲場解析。
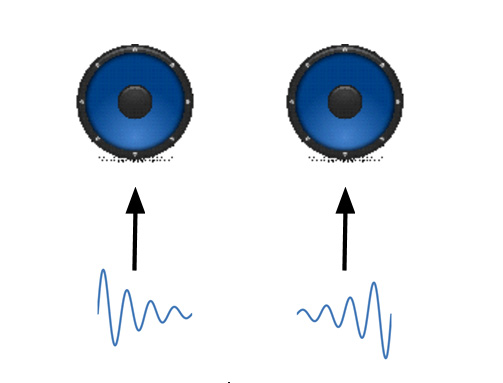
圖2:兩個或多個信號通道分配到揚聲器(立體聲)
項目速率(采樣率):在一秒內對連續時間信號的采樣次數,然后將其轉換為離散時間信號(數值)。采樣的度量單位是S/s(即每秒采樣數)。
由于音頻信號是模擬信號,我們需要將其轉換為數字信號,以便由計算機進行處理。我們可以使用下面的采樣定理完成此操作。
我們假設有一個模擬信號,如下圖所示。想象一下,您需要向您的朋友描述這個信號。這項任務并不是最簡單的任務。在這種情況下,將信號描述為數字序列將更加簡單。
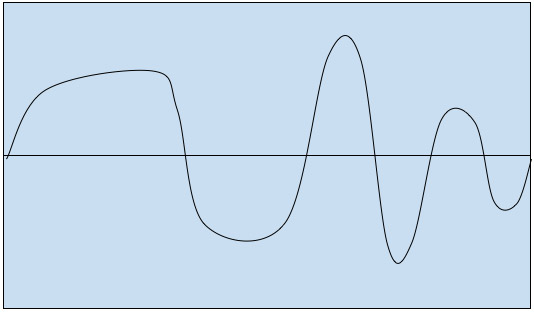
圖3:模擬信號示例
每個樣本都以其自身的幅度進行描述。用戶可以根據自己的喜好選擇采樣率。下圖顯示了如何根據采樣定理將模擬信號轉換為數字信號。
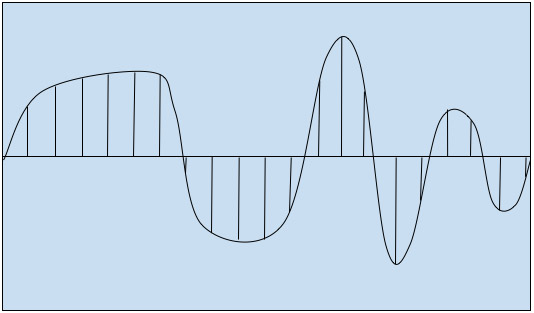
圖4:模擬信號轉換為數字信號
采樣率必須根據人類聽覺范圍——20Hz至20000Hz——進行選擇。為了能夠獲得特定信號(即準確聲音)的所有必要信息,我們的采樣率必須滿足以下奈奎斯特-香農定理才能將其轉換為離散時間信號:
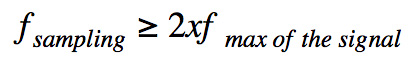
采樣率必須大于信號頻譜中最高(最大)頻率的兩倍。在我們的例子中,最大頻率為20000Hz。
本項目我們選擇48000Hz——這是處理音頻信號時的一個標準值。在這種情況下,信號處理時連續時間信號中的所有信息都沒有丟失。
說到采樣率,一般有2種情況:
過采樣 – 維基百科
采樣頻率顯著高于奈奎斯特速率。從理論上講,如果以奈奎斯特速率或高于奈奎斯特速率進行采樣,就可以完美重建有限帶寬的信號。奈奎斯特速率的定義為信號中最高頻率分量的兩倍。
欠采樣 (或走樣) – 維基百科
這種技術以低于其奈奎斯特速率(高截止頻率的兩倍)的采樣率采樣帶通濾波信號,但是仍然能夠重建信號。如果以欠采樣方式采樣一個帶通信號時,采樣點與高頻信號的低頻分量采樣點無法區分(即信號變得難以區分)。
接下來,我們通過正弦波進行演示。
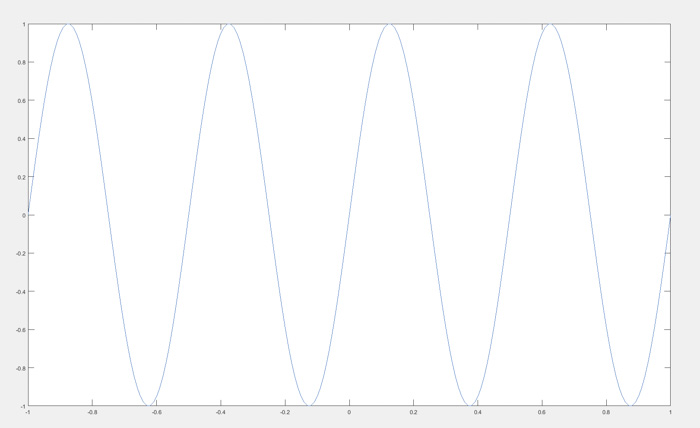
圖5:一個正弦波(在MATLAB中繪制)
這是一個頻率為2Hz、時域為[-1,1]的正弦波。該波形包含4個周期,這意味著每0.5秒(1/2 Hz)發生一個周期。我們會對這個信號實施多種采樣案例,以了解采樣的工作原理。
采樣點數表示在一個周期內添加了多少個點,并這些點會用插值算法連接起來。一個周期的最小點數應為20,否則線性插值信號看起來就會失真。這尤其適用于平滑的模擬信號,采樣后會丟失圓邊圖案。點的數量越多,采樣信號越準確。
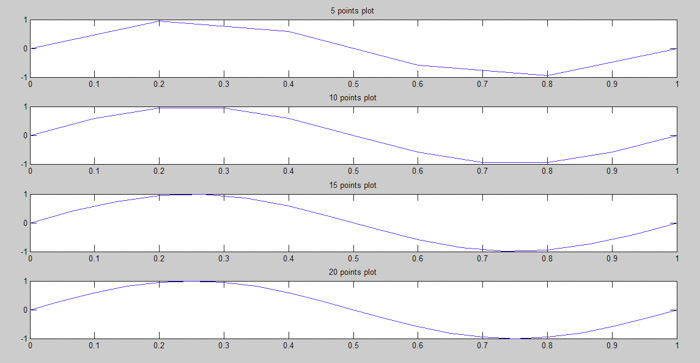
圖6:正弦波的必要點數(在MATLAB中繪制)
在本教程中,我們會在MATLAB中繪制一些正弦波,并觀察采樣頻率不同時這些正弦波的行為。在語音信號系列的第二部分中,我們將使用MATLAB進行傅立葉分析。使用Arduino時,MATLAB也是一個非常有用的工具,因為它可以利用串行接口很好地進行通信。我們將在本系列的第三部分中詳細介紹如何用Arduino錄制語音信號并在MATLAB中進行處理。
對于那些不完全熟悉MATLAB的人,繪制函數的一般步驟如下所示:
要創建腳本或函數,請轉到 [HOME] → [New] ,然后選擇“Script”(腳本)或“Function”(函數)。
要繪制圖7中所示的正弦波,我們需要創建一個Script。復制并粘貼以下代碼:
f = 1 points = 5; t = 0:1/points:1; wave = sin(2*pi*f*t); subplot(4,1,1) plot(t,wave) title('5 points plot') points1 = 10; t = 0:1/points1:1; wave1 = sin(2*pi*f*t); subplot(4,1,2) plot(t,wave1) title('10 points plot') points2 = 15; t = 0:1/points2:1; wave2 = sin(2*pi*f*t); subplot(4,1,3) plot(t,wave2) title('15 points plot') points3 = 20; t = 0:1/points3:1; wave3 = sin(2*pi*f*t); subplot(4,1,4) plot(t,wave3) title('20 points plot')
要查看結果,您只需按 Run 按鈕即可。
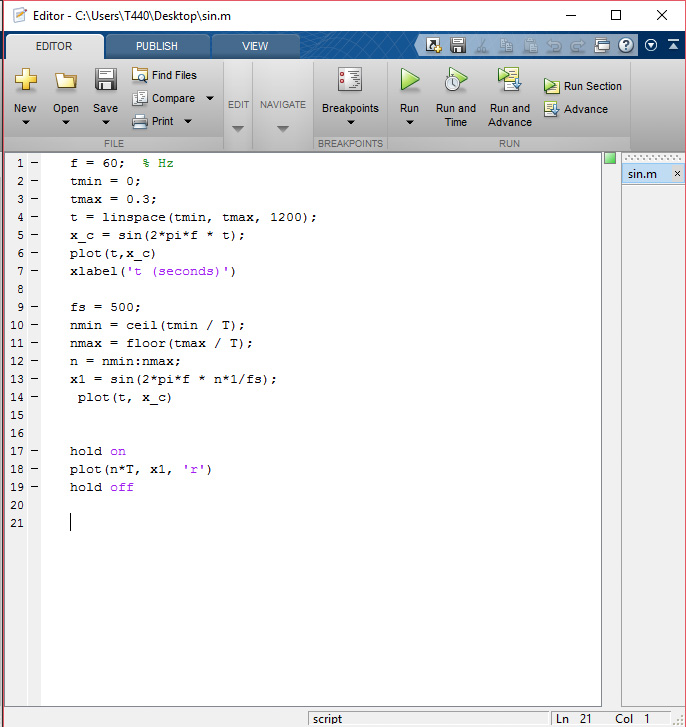
我們還需要創建另一個圖——就在剛剛創建的圖上繪制,以查看我們對信號進行采樣時信號的形式如何變化。信號長度我們選取0.5秒,但是頻率增加為60。我們處理的點數也修改為頻率數的20倍。假設在這個區間內我們以50Hz的頻率進行采樣;這意味著每個點都位于T=1/50(其中T是采樣周期)處。圖7中的小紅點就是信號上的采樣點。
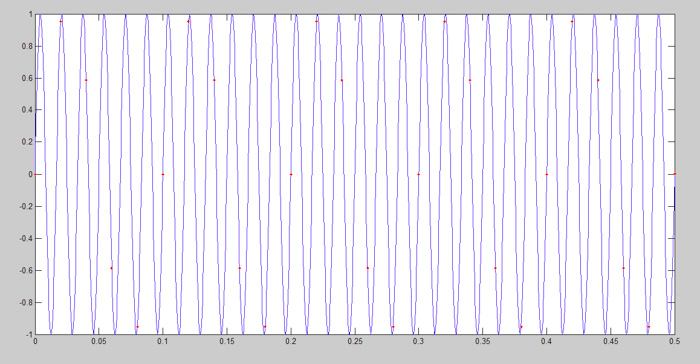
圖7:欠采樣正弦波
在圖7中,由于缺少采樣點,我們無法掌握原始信號的形狀。連接采樣點后,由于信號的點不足,紅色信號的形狀異常(圖8)。這些點無法以正弦形式插值,紅色信號不能重建藍色信號。
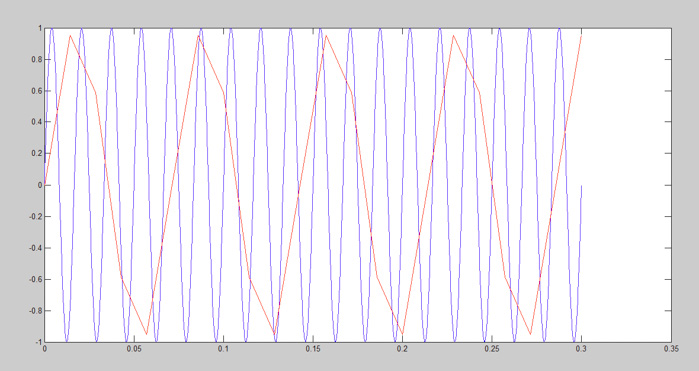
圖8:正弦波,fs = 50 Hz
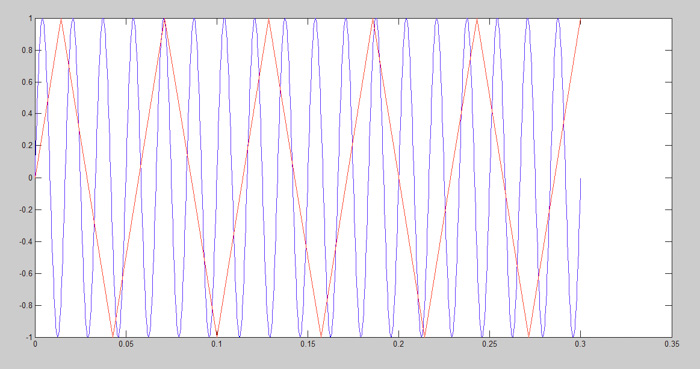
圖9:正弦波,fs = 240 Hz
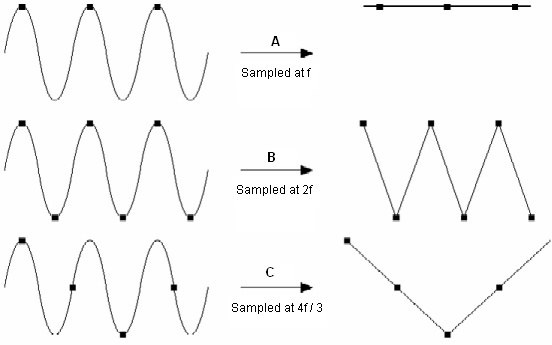
圖10: 采樣頻率示例
如圖9和圖10所示,當我們以2倍頻率進行采樣時,圖中的唯一采樣點就是頂部和底部的最大值。根據采樣定理,這兩個點足以重建信號。
第2步:處理語音信號
上文介紹了信號及其屬性。現在我們需要用一個實際例子進行測試。Audacity的錄音屬性如下:
采樣率: 48000 Hz
位數: 16
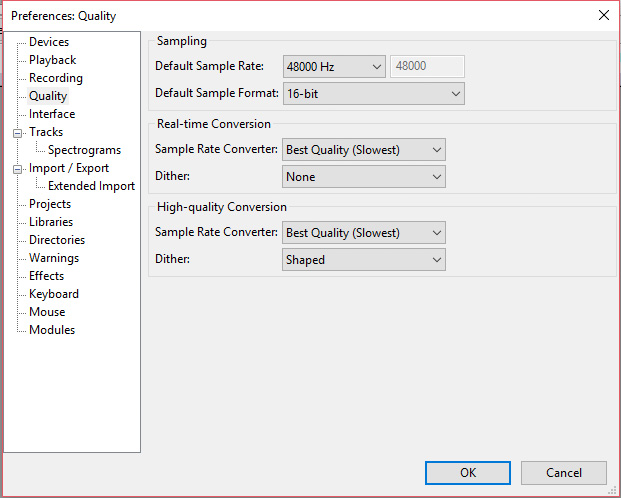
圖11:Audacity錄制所需的設置
信號長度應至少為10秒左右(項目會進行許多處理,因此不建議超過20秒)。
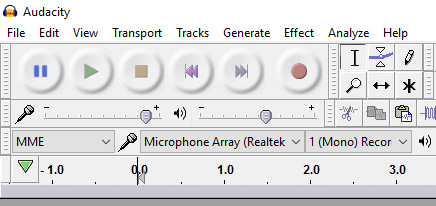
圖12:Audacity
與其他錄制平臺相比,Audacity非常直觀。在下圖中,您可以看到一個中間有圓圈的紅色按鈕(record 圖標) – 這就是開始錄音的按鈕。要停止錄制,只需按下黃色方塊按鈕(stop 按鈕)即可。程序會記錄錄音的聲波,并將其繪制處理,如下圖所示。
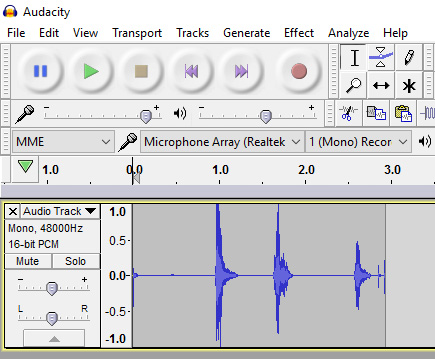
圖13:錄制的音頻信號
第1部分簡要介紹了數字信號處理理論。我們使用MATLAB探索了不同的信號波形,并用Audacity錄制了自己的聲音。在下一個教程中,我們將深入探討“處理”的更多細節。我們將涉及各種算法和時頻域。我們會繼續利用MATLAB作為函數編寫的主要工具,以處理我們錄制的語音并獲得分析結果。
審核編輯:湯梓紅
-
matlab
+關注
關注
185文章
2980瀏覽量
230811 -
數字信號處理
+關注
關注
15文章
563瀏覽量
45948 -
語音信號
+關注
關注
3文章
70瀏覽量
22869
發布評論請先 登錄
相關推薦

















評論