摘要:在深度神經(jīng)網(wǎng)絡(luò)訓(xùn)練的過程中,由于網(wǎng)絡(luò)中參數(shù)變化而引起網(wǎng)絡(luò)中間層數(shù)據(jù)分布發(fā)生變化的這一過程被稱為內(nèi)部協(xié)變量偏移(Internal Covariate Shift),而 BN 可以解決這個問題。
一,數(shù)學(xué)基礎(chǔ)
1.1,概率密度函數(shù)
隨機(jī)變量(random variable)是可以隨機(jī)地取不同值的變量。隨機(jī)變量可以是離散的或者連續(xù)的。簡單起見,本文用大寫字母 XX表示隨機(jī)變量,小寫字母 xx表示隨機(jī)變量能夠取到的值。例如,x1x1 和 x2x2 都是隨機(jī)變量 XX可能的取值。隨機(jī)變量必須伴隨著一個概率分布來指定每個狀態(tài)的可能性。
概率分布(probability distribution)用來描述隨機(jī)變量或一簇隨機(jī)變量在每一個可能取到的狀態(tài)的可能性大小。我們描述概率分布的方式取決于隨機(jī)變量是離散的還是連續(xù)的。 當(dāng)我們研究的對象是連續(xù)型隨機(jī)變量時,我們用概率密度函數(shù)(probability density function, PDF)而不是概率質(zhì)量函數(shù)來描述它的概率分布。
1.2,正態(tài)分布
當(dāng)我們不知道數(shù)據(jù)真實(shí)分布時使用正態(tài)分布的原因之一是,正態(tài)分布擁有最大的熵,我們通過這個假設(shè)來施加盡可能少的結(jié)構(gòu)。 實(shí)數(shù)上最常用的分布就是正態(tài)分布 (normal distribution),也稱為高斯分布 (Gaussian distribution)。 如果隨機(jī)變量 XX,服從位置參數(shù)為 μμ、尺度參數(shù)為 σσ的概率分布,且其概率密度函數(shù)為: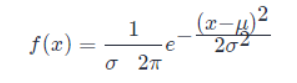
則這個隨機(jī)變量就稱為正態(tài)隨機(jī)變量,正態(tài)隨機(jī)變量服從的概率分布就稱為正態(tài)分布,記作: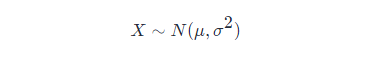
如果位置參數(shù) μ=0μ=0,尺度參數(shù) σ=1σ=1 時,則稱為標(biāo)準(zhǔn)正態(tài)分布,記作: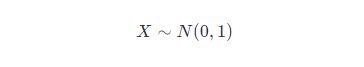
此時,概率密度函數(shù)公式簡化為: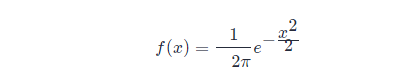
正太分布的數(shù)學(xué)期望值或期望值 μμ等于位置參數(shù),決定了分布的位置;其方差 σ2σ2 的開平方或標(biāo)準(zhǔn)差 σσ等于尺度參數(shù),決定了分布的幅度。
正太分布的概率密度函數(shù)曲線呈鐘形,常稱之為鐘形曲線,如下圖所示: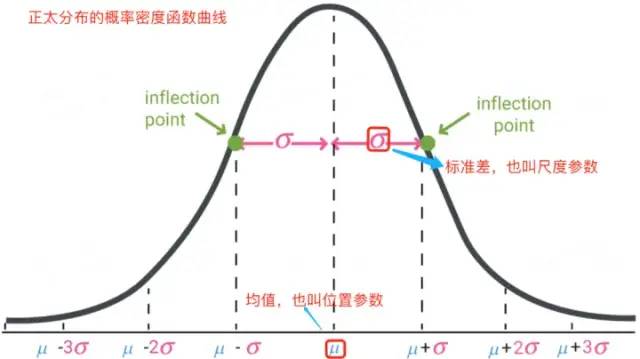
可視化正態(tài)分布,可直接通過 np.random.normal 函數(shù)生成指定均值和標(biāo)準(zhǔn)差的正態(tài)分布隨機(jī)數(shù),然后基于 matplotlib + seaborn 庫 kdeplot 函數(shù)繪制概率密度曲線。
示例代碼如下所示:

以上代碼直接運(yùn)行后,輸出結(jié)果如下圖:
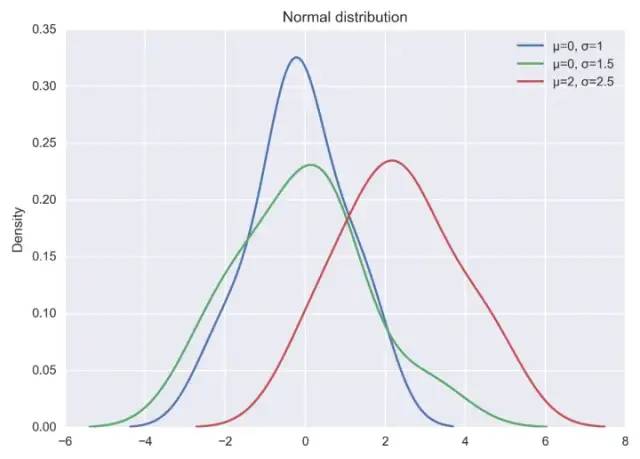
當(dāng)然也可以自己實(shí)現(xiàn)正太分布的概率密度函數(shù),代碼和程序輸出結(jié)果如下:

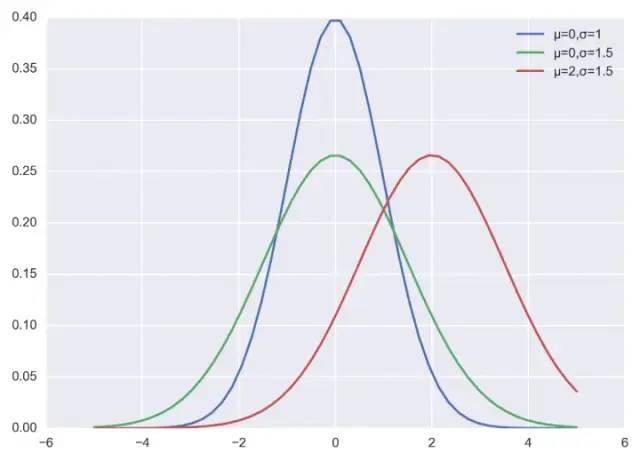
二,背景
訓(xùn)練深度神經(jīng)網(wǎng)絡(luò)的復(fù)雜性在于,因?yàn)榍懊娴膶拥膮?shù)會發(fā)生變化導(dǎo)致每層輸入的分布在訓(xùn)練過程中會發(fā)生變化。這又導(dǎo)致模型需要需要較低的學(xué)習(xí)率和非常謹(jǐn)慎的參數(shù)初始化策略,從而減慢了訓(xùn)練速度,并且具有飽和非線性的模型訓(xùn)練起來也非常困難。 網(wǎng)絡(luò)層輸入數(shù)據(jù)分布發(fā)生變化的這種現(xiàn)象稱為內(nèi)部協(xié)變量轉(zhuǎn)移,BN 就是來解決這個問題。
2.1,如何理解 Internal Covariate Shift
在深度神經(jīng)網(wǎng)絡(luò)訓(xùn)練的過程中,由于網(wǎng)絡(luò)中參數(shù)變化而引起網(wǎng)絡(luò)中間層數(shù)據(jù)分布發(fā)生變化的這一過程被稱在論文中稱之為內(nèi)部協(xié)變量偏移(Internal Covariate Shift)。 那么,為什么網(wǎng)絡(luò)中間層數(shù)據(jù)分布會發(fā)生變化呢? 在深度神經(jīng)網(wǎng)絡(luò)中,我們可以將每一層視為對輸入的信號做了一次變換(暫時不考慮激活,因?yàn)榧せ詈瘮?shù)不會改變輸入數(shù)據(jù)的分布):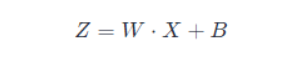
其中 WW和 BB是模型學(xué)習(xí)的參數(shù),這個公式涵蓋了全連接層和卷積層。 隨著 SGD 算法更新參數(shù),和網(wǎng)絡(luò)的每一層的輸入數(shù)據(jù)經(jīng)過公式 5 的運(yùn)算后,其 ZZ的分布一直在變化,因此網(wǎng)絡(luò)的每一層都需要不斷適應(yīng)新的分布,這一過程就被叫做 Internal Covariate Shift。 而深度神經(jīng)網(wǎng)絡(luò)訓(xùn)練的復(fù)雜性在于每層的輸入受到前面所有層的參數(shù)的影響 — 因此當(dāng)網(wǎng)絡(luò)變得更深時,網(wǎng)絡(luò)參數(shù)的微小變化就會被放大。
2.2,Internal Covariate Shift 帶來的問題
網(wǎng)絡(luò)層需要不斷適應(yīng)新的分布,導(dǎo)致網(wǎng)絡(luò)學(xué)習(xí)速度的降低。
網(wǎng)絡(luò)層輸入數(shù)據(jù)容易陷入到非線性的飽和狀態(tài)并減慢網(wǎng)絡(luò)收斂,這個影響隨著網(wǎng)絡(luò)深度的增加而放大。
隨著網(wǎng)絡(luò)層的加深,后面網(wǎng)絡(luò)輸入 xx越來越大,而如果我們又采用 Sigmoid 型激活函數(shù),那么每層的輸入很容易移動到非線性飽和區(qū)域,此時梯度會變得很小甚至接近于 00,導(dǎo)致參數(shù)的更新速度就會減慢,進(jìn)而又會放慢網(wǎng)絡(luò)的收斂速度。 飽和問題和由此產(chǎn)生的梯度消失通常通過使用修正線性單元激活(ReLU (x)=max (x,0)ReLU(x)=max(x,0)),更好的參數(shù)初始化方法和小的學(xué)習(xí)率來解決。
然而,如果我們能保證非線性輸入的分布在網(wǎng)絡(luò)訓(xùn)練時保持更穩(wěn)定,那么優(yōu)化器將不太可能陷入飽和狀態(tài),進(jìn)而訓(xùn)練也將加速。
2.3,減少 Internal Covariate Shift 的一些嘗試
白化(Whitening): 即輸入線性變換為具有零均值和單位方差,并去相關(guān)。 白化過程由于改變了網(wǎng)絡(luò)每一層的分布,因而改變了網(wǎng)絡(luò)層中本身數(shù)據(jù)的表達(dá)能力。底層網(wǎng)絡(luò)學(xué)習(xí)到的參數(shù)信息會被白化操作丟失掉,而且白化計算成本也高。
標(biāo)準(zhǔn)化(normalization)
Normalization 操作雖然緩解了 ICS 問題,讓每一層網(wǎng)絡(luò)的輸入數(shù)據(jù)分布都變得穩(wěn)定,但卻導(dǎo)致了數(shù)據(jù)表達(dá)能力的缺失。
三,批量歸一化(BN)
3.1,BN 的前向計算
論文中給出的 Batch Normalizing Transform 算法計算過程如下圖所示。其中輸入是一個考慮一個大小為 mm的小批量數(shù)據(jù) BB。
論文中的公式不太清晰,下面我給出更為清晰的 Batch Normalizing Transform 算法計算過程。
設(shè) mm表示 batch_size 的大小,nn表示 features 數(shù)量,即樣本特征值數(shù)量。在訓(xùn)練過程中,針對每一個 batch 數(shù)據(jù),BN 過程進(jìn)行的操作是,將這組數(shù)據(jù) normalization,之后對其進(jìn)行線性變換,具體算法步驟如下: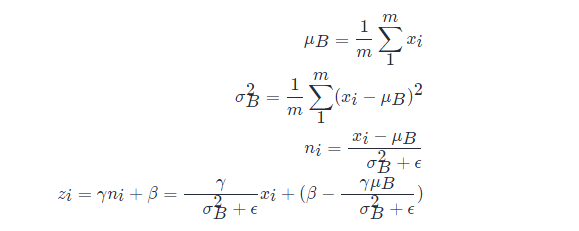
以上公式乘法都為元素乘,即 element wise 的乘法。其中,參數(shù) γ,βγ,β是訓(xùn)練出來的, ??是為零防止 σB2σB2 為 00 ,加的一個很小的數(shù)值,通常為 1e-5。公式各個符號解釋如下: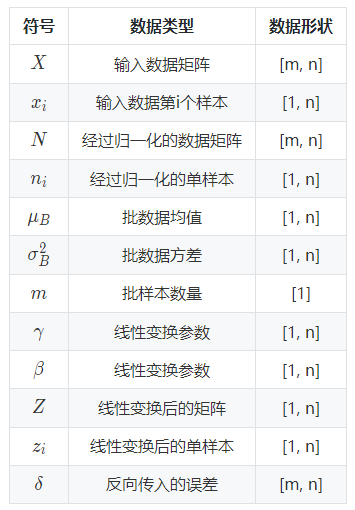
其中: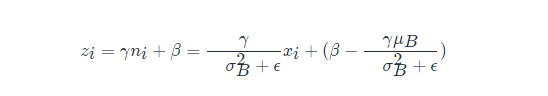
可以看出 BN 本質(zhì)上是做線性變換。
3.2,BN 層如何工作
在論文中,訓(xùn)練一個帶 BN 層的網(wǎng)絡(luò), BN 算法步驟如下圖所示:
在訓(xùn)練期間,我們一次向網(wǎng)絡(luò)提供一小批數(shù)據(jù)。在前向傳播過程中,網(wǎng)絡(luò)的每一層都處理該小批量數(shù)據(jù)。BN 網(wǎng)絡(luò)層按如下方式執(zhí)行前向傳播計算: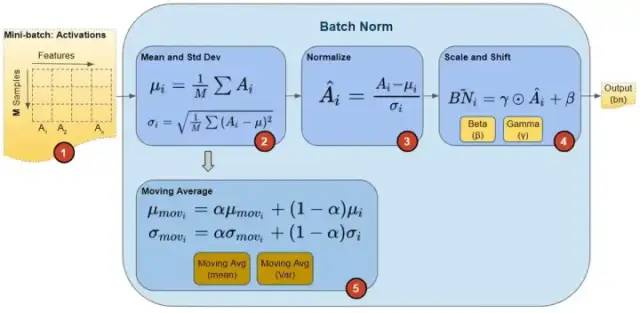
注意,圖中計算均值與方差的無偏估計方法是吳恩達(dá)在 Coursera 上的 Deep Learning 課程上提出的方法:對 train 階段每個 batch 計算的 mean/variance 采用指數(shù)加權(quán)平均來得到 test 階段 mean/variance 的估計。 在訓(xùn)練期間,它只是計算此 EMA,但不對其執(zhí)行任何操作。
在訓(xùn)練結(jié)束時,它只是將該值保存為層狀態(tài)的一部分,以供在推理階段使用。 如下圖可以展示 BN 層的前向傳播計算過程數(shù)據(jù)的 shape ,紅色框出來的單個樣本都指代單個矩陣,即運(yùn)算都是在單個矩陣運(yùn)算中計算的。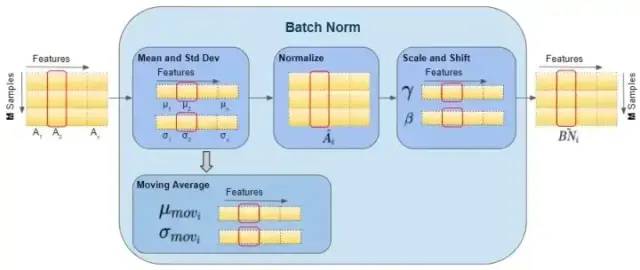
BN 的反向傳播過程中,會更新 BN 層中的所有 ββ和 γγ參數(shù)。
3.3,訓(xùn)練和推理式的 BN 層
批量歸一化(batch normalization)的 “批量” 兩個字,表示在模型的迭代訓(xùn)練過程中,BN 首先計算小批量( mini-batch,如 32)的均值和方差。但是,在推理過程中,我們只有一個樣本,而不是一個小批量。在這種情況下,我們該如何獲得均值和方差呢? 第一種方法是,使用的均值和方差數(shù)據(jù)是在訓(xùn)練過程中樣本值的平均,即: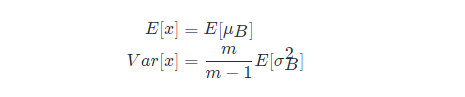
這種做法會把所有訓(xùn)練批次的 μμ和 σσ都保存下來,然后在最后訓(xùn)練完成時(或做測試時)做下平均。 第二種方法是使用類似動量的方法,訓(xùn)練時,加權(quán)平均每個批次的值,權(quán)值 αα可以為 0.9: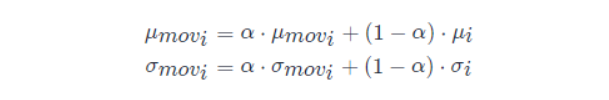
推理或測試時,直接使用模型文件中保存的 μmoviμmovi 和 σmoviσmovi 的值即可。
3.4,實(shí)驗(yàn)
BN 在 ImageNet 分類數(shù)據(jù)集上實(shí)驗(yàn)結(jié)果是 SOTA 的,如下表所示: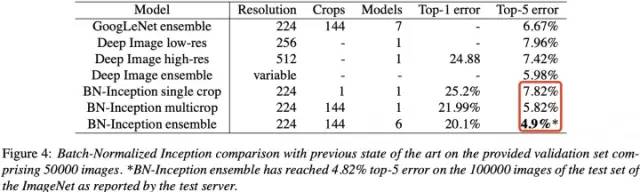
3.5,BN 層的優(yōu)點(diǎn)
BN 使得網(wǎng)絡(luò)中每層輸入數(shù)據(jù)的分布相對穩(wěn)定,加速模型訓(xùn)練和收斂速度。
批標(biāo)準(zhǔn)化可以提高學(xué)習(xí)率。在傳統(tǒng)的深度網(wǎng)絡(luò)中,學(xué)習(xí)率過高可能會導(dǎo)致梯度爆炸或梯度消失,以及陷入差的局部最小值。批標(biāo)準(zhǔn)化有助于解決這些問題。
通過標(biāo)準(zhǔn)化整個網(wǎng)絡(luò)的激活值,它可以防止層參數(shù)的微小變化隨著數(shù)據(jù)在深度網(wǎng)絡(luò)中的傳播而放大。例如,這使 sigmoid 非線性更容易保持在它們的非飽和狀態(tài),這對訓(xùn)練深度 sigmoid 網(wǎng)絡(luò)至關(guān)重要,但在傳統(tǒng)上很難實(shí)現(xiàn)。
BN 允許網(wǎng)絡(luò)使用飽和非線性激活函數(shù)(如 sigmoid,tanh 等)進(jìn)行訓(xùn)練,其能緩解梯度消失問題。
不需要 dropout 和 LRN(Local Response Normalization)層來實(shí)現(xiàn)正則化。批標(biāo)準(zhǔn)化提供了類似丟棄的正則化收益,因?yàn)橥ㄟ^實(shí)驗(yàn)可以觀察到訓(xùn)練樣本的激活受到同一小批量樣例隨機(jī)選擇的影響。
減少對參數(shù)初始化方法的依賴。
審核編輯:劉清
-
神經(jīng)網(wǎng)絡(luò)
+關(guān)注
關(guān)注
42文章
4779瀏覽量
101054 -
ICS
+關(guān)注
關(guān)注
0文章
36瀏覽量
18162
原文標(biāo)題:詳解神經(jīng)網(wǎng)絡(luò)基礎(chǔ)部件BN層
文章出處:【微信號:OSC開源社區(qū),微信公眾號:OSC開源社區(qū)】歡迎添加關(guān)注!文章轉(zhuǎn)載請注明出處。
發(fā)布評論請先 登錄
相關(guān)推薦




 淺析神經(jīng)網(wǎng)絡(luò)基礎(chǔ)部件BN層
淺析神經(jīng)網(wǎng)絡(luò)基礎(chǔ)部件BN層










評論