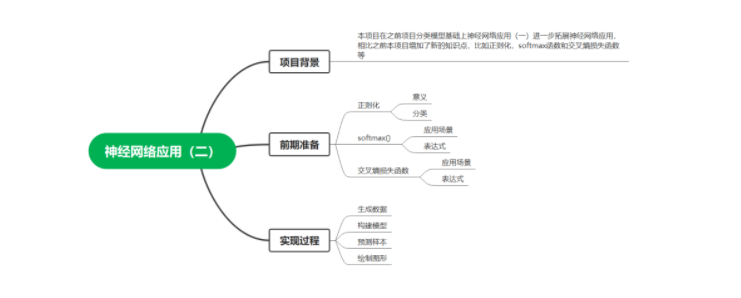
一.項目背景
本項目在之前項目分類模型基礎上神經網絡應用(一)進一步拓展神經網絡應用,相比之前本項目增加了新的知識點,比如正則化,softmax函數和交叉熵損失函數等。
二.前期準備
1.正則化
1)解釋:在機器學習中為了防止模型過擬合(簡單說就是在訓練集上樣本表現的
很好,在測試集上表現的很差),經常需要進行正則化,所謂正則化簡單來說就是讓模
型系數變得相對小一點,防止數據稍微變化引起模型圖形曲線較大波動,總之一句話,
讓模型曲線表現更加平穩。
2)分類:正則化總體分類為L1正則化和L2正則化。兩者區別在于范數級別不同,
L2正則化是||w||2,L1正則化是||w||1范數,并且L2正則傾向于系數W盡量均衡(非
零分量個數盡量多),L1正則化使W分類盡量稀疏(非零分量個數盡量少),我們以線
性回歸為例,簡單說明一下。


【注】正則項不包括截距項。
2.Softmax函數
1)Softmax經常被應用在多分類任務的神經網絡中的輸出層,簡單理解可以認為
Softmax輸出的是幾個類別選擇的概率。比如我有一個二分類任務,Softmax函數可以
根據它們相對的大小,輸出二個類別選取的概率,并且概率和為1。表達式如下,Si代
表的是第i個神經元的輸出。
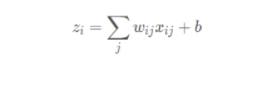
softmax函數
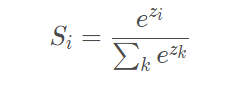
3.交叉熵損失函數
在神經網絡反向傳播中需要損失函數,損失函數其實表示的是真實值與網絡的估計
值的誤差,有了這個誤差我們才能知道怎樣去修改網絡中的權重。損失函數可以有很多
形式,這里用的是交叉熵函數,主要是由于這個求導結果比較簡單,易于計算,并且交
叉熵解決某些損失函數學習緩慢的問題,函數表達式如下
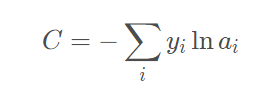
它的導數推到過程我們就不再說明,網上有很多資料大家可以參考,針對本項目分類
模型,我們最終結果為如下,也就是我們的預測概率值減去目標值。
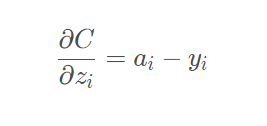
三.實現過程
1.生成數據
#生成數據
def generate_data():
#設定種子數,保定生成數據相同
np.random.seed(0)
#生成數據集和標簽,noise表示產生噪音
X, y = datasets.make_moons(200, noise=0.20)
#返回數據集
return X, y
2.構建模型
#計算損失函數
def calculate_loss(model, X, y):
#訓練樣本個數
num_examples = len(X) # training set size
#加載模型參數
W1, b1, W2, b2 = model['W1'], model['b1'], model['W2'], model['b2']
#前向傳播
z1 = X.dot(W1) + b1
a1 = np.tanh(z1)
z2 = a1.dot(W2) + b2
exp_scores = np.exp(z2)
#softmax函數歸一化
probs = exp_scores / np.sum(exp_scores, axis=1, keepdims=True)
#定義交叉熵損失函數
corect_logprobs = -np.log(probs[range(num_examples), y])
#計算總的損失函數
data_loss = np.sum(corect_logprobs)
#L2正則化,防止過擬合
data_loss += Config.reg_lambda / 2 * (np.sum(np.square(W1)) + np.sum(np.square(W2)))
#除以樣本總數
return 1. / num_examples * data_loss
#構建模型
def build_model(X, y, nn_hdim, num_passes=20000, print_loss=False):
#樣本個數
num_examples = len(X)
#記錄隨機中子數
np.random.seed(0)
#初始化神經網絡參數
W1 = np.random.randn(Config.nn_input_dim, nn_hdim) / np.sqrt(Config.nn_input_dim)
b1 = np.zeros((1, nn_hdim))
W2 = np.random.randn(nn_hdim, Config.nn_output_dim) / np.sqrt(nn_hdim)
b2 = np.zeros((1, Config.nn_output_dim))
#存儲模型參數
model = {}
#遍歷每一輪
for i in range(0, num_passes):
#前向傳播
z1 = X.dot(W1) + b1
#函數表達式(e(z)-e(-z))/(e(z)+e(-z))
#隱藏層輸出
a1 = np.tanh(z1)
z2 = a1.dot(W2) + b2
#輸出層輸出
exp_scores = np.exp(z2)
#計算概率
probs = exp_scores / np.sum(exp_scores, axis=1, keepdims=True)
#反向傳播
delta3 = probs
#計算損失函數導數
delta3[range(num_examples), y] -= 1
#計算w2梯度
dW2 = (a1.T).dot(delta3)
#計算b2梯度
db2 = np.sum(delta3, axis=0, keepdims=True)
#計算輸入層到隱藏層總誤差
delta2 = delta3.dot(W2.T) * (1 - np.power(a1, 2))
#計算w1梯度
dW1 = np.dot(X.T, delta2)
#計算b1梯度
db1 = np.sum(delta2, axis=0)
#正則化系數w(只對w進行正則化,b不改變)
dW2 += Config.reg_lambda * W2
dW1 += Config.reg_lambda * W1
#更新參數
W1 += -Config.epsilon * dW1
b1 += -Config.epsilon * db1
W2 += -Config.epsilon * dW2
b2 += -Config.epsilon * db2
#存儲模型參數
model = {'W1': W1, 'b1': b1, 'W2': W2, 'b2': b2}
#輸出損失函數
if print_loss and i % 1000 == 0:
print("Loss after iteration %i: %f" % (i, calculate_loss(model, X, y)))
#返回模型參數
return model
3.預測樣本
#預測樣本
def predict(model, x):
#加載模型參數
W1, b1, W2, b2 = model['W1'], model['b1'], model['W2'], model['b2']
#前向傳播
z1 = x.dot(W1) + b1
a1 = np.tanh(z1)
z2 = a1.dot(W2) + b2
#計算總體輸出
exp_scores = np.exp(z2)
#softmax函數
probs = exp_scores / np.sum(exp_scores, axis=1, keepdims=True)
#返回預測概率最大值對應標簽
return np.argmax(probs, axis=1)
4.繪制圖形可視化
#繪制邊界線
def plot_decision_boundary(pred_func, X, y):
#分別設置間隔
x_min, x_max = X[:, 0].min() - 0.5, X[:, 0].max() + 0.5
y_min, y_max = X[:, 1].min() - 0.5, X[:, 1].max() + 0.5
#步長
h = 0.01
#生成網格數據
xx, yy = np.meshgrid(np.arange(x_min, x_max, h), np.arange(y_min, y_max, h))
#預測整個網格z值
Z = pred_func(np.c_[xx.ravel(), yy.ravel()])
Z = Z.reshape(xx.shape)
#繪制分割線
plt.contourf(xx,
yy,
Z,
cmap=plt.cm.Spectral)
#繪制散點圖
plt.scatter(X[:, 0],
X[:, 1],
c=y,
cmap=plt.cm.Spectral)
#顯示圖形
plt.show()
#可視化函數
def visualize(X, y, model):
#繪制圖形
plot_decision_boundary(lambda x:predict(model,x), X, y)
#設置標題
plt.title("Neural Network")
#主函數
def main():
#生成數據
X, y = generate_data()
#構建模型
model = build_model(X, y, 3, print_loss=True)
#可視化
visualize(X, y, model)
#預測準確樣本數
accuracy=0
#設定種子數,保定生成數據相同
np.random.seed(1)
#生成數據集和標簽,noise表示產生噪音
X_test, y = datasets.make_moons(200, noise=0.20)
#驗證測試集
for i in range(len(X_test)):
#預測測試集
if y[i]==predict(model,X_test[i]):
#預測準確數目
accuracy+=1
#輸出準確率
print("Accuracy:",float(accuracy)/len(X_test))
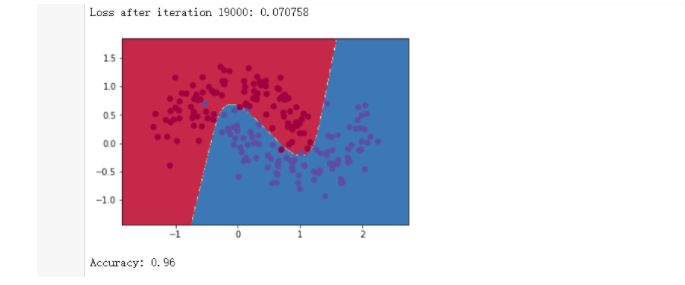
結論:準確率為96%(這里測試集數據我們添加了噪音),如果在產生測試集數據時取掉
noise參數(也就是說取掉噪音數據),準確率會更高。
聲明:本文內容及配圖由入駐作者撰寫或者入駐合作網站授權轉載。文章觀點僅代表作者本人,不代表電子發燒友網立場。文章及其配圖僅供工程師學習之用,如有內容侵權或者其他違規問題,請聯系本站處理。
舉報投訴
-
神經網絡
+關注
關注
42文章
4771瀏覽量
100772 -
函數
+關注
關注
3文章
4331瀏覽量
62622 -
Softmax
+關注
關注
0文章
9瀏覽量
2514
發布評論請先 登錄
相關推薦




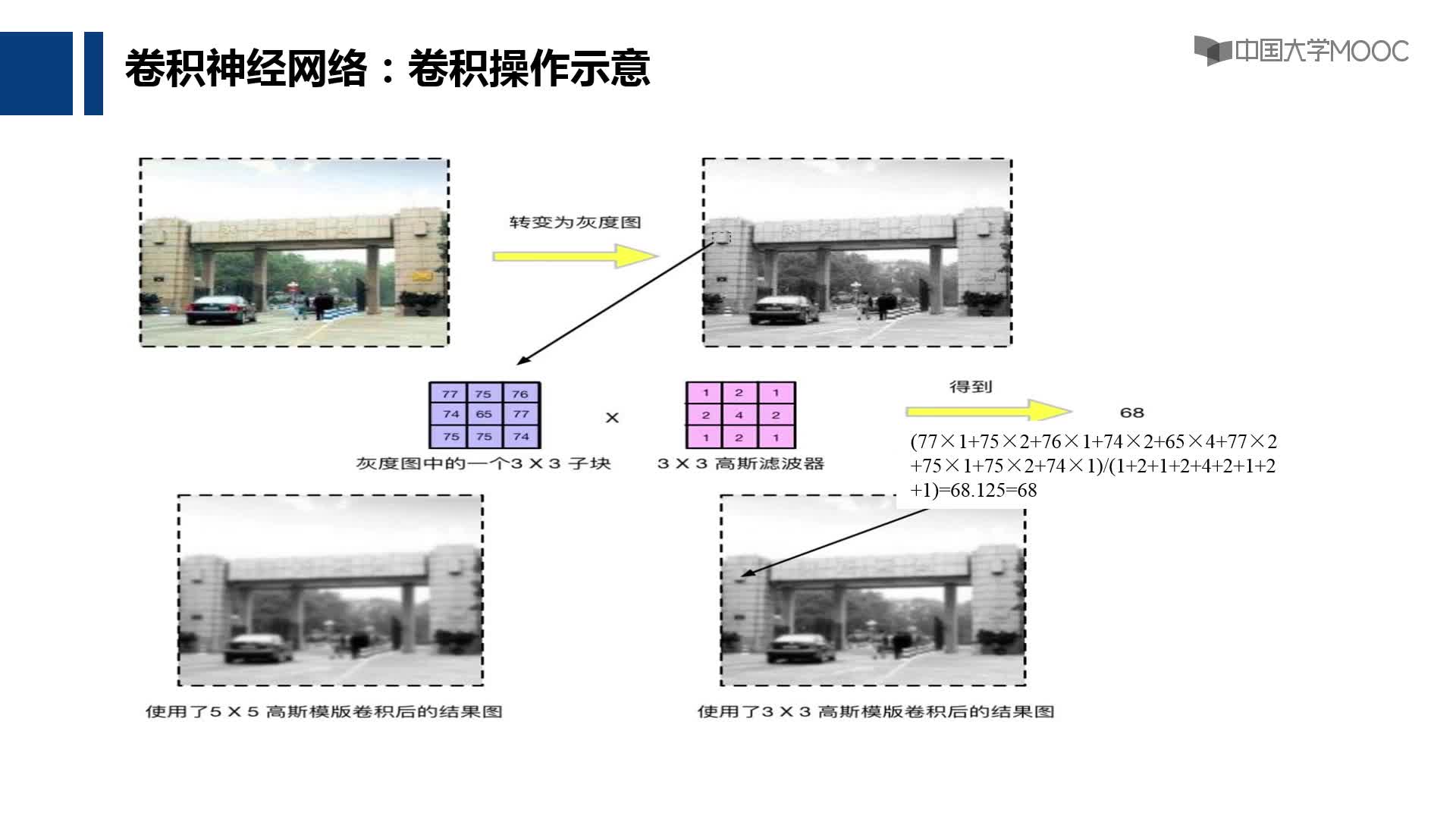





【PYNQ-Z2申請】基于PYNQ的卷積神經網絡加速
,得到訓練參數2、利用開發板arm與FPGA聯合的特性,在arm端實現圖像預處理已經卷積核神經網絡的池化、激活函數和全連接,在FPGA端實現卷積運算3、對整個系統進行調試。4、在基本實現系統的基礎上
發表于 12-19 11:37
用Python從頭實現一個神經網絡來理解神經網絡的原理2
有個事情可能會讓初學者驚訝:神經網絡模型并不復雜!『神經網絡』這個詞讓人覺得很高大上,但實際上神經網絡算法要比人們想象的簡單。
這篇文章完全是為新手準備的。我們會通過用Python從頭實現一個




 什么是神經網絡應用-2
什么是神經網絡應用-2










評論