要了解積分非線性誤差的影響，最直接的方法是分析簡單的正弦波，并將眾所周知的三角恒等式應用于包含INL誤差的非理想模數輸出傳遞函數。

對于理想的系統，具有振幅A和頻率fo的單音正弦波，

X(t) = Asin(2π fot)

使用周期為T的ADC采樣會產生離散信號：

X[n]=Asin(2π fonT),

其中 X[n] 是從每 T 秒對 X（t） 進行均勻采樣獲得的離散時間信號。倒數 1/T = F 稱為采樣率或采樣頻率。

一類特別重要的系統由線性和時間不變的系統組成，或“LTI”。這兩個屬性相結合，為此類系統提供了特別方便的表示形式。最重要的是，LTI 系統 X[n] 的輸入和輸出 Y[n] 之間的關系可以通過卷積和給出。卷積是分析和描述LTI系統的基礎。在這個例子中，我們將只分析系統的線性度。

線性系統是滿足疊加原理的系統。簡單地說，疊加原理要求系統對信號加權和的響應等于系統對每個單獨輸入信號的響應（輸出）的相應加權和。疊加特性大大簡化了線性系統的分析。由于分解屬性，您可以分別計算輸出的不同組件。

將理想的ADC傳輸曲線與具有INL誤差的傳輸曲線進行比較，很容易演示具有INL誤差的系統如何產生非線性輸出。當輸出 Y3[n] = X1[n] + X2[n] 時，輸出 Y3[n] 不等于輸出 Y1[n] +Y2[n] 的總和。更準確地說，F（X1 + X2）≠F（X1）+ F（X2）。因此，非線性誤差會產生額外的、不需要的內部生成的正弦波，從而增加設計成本和濾波器復雜性。（電氣工程師將內部生成的正弦波的這種影響視為互調失真。

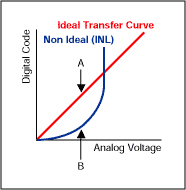
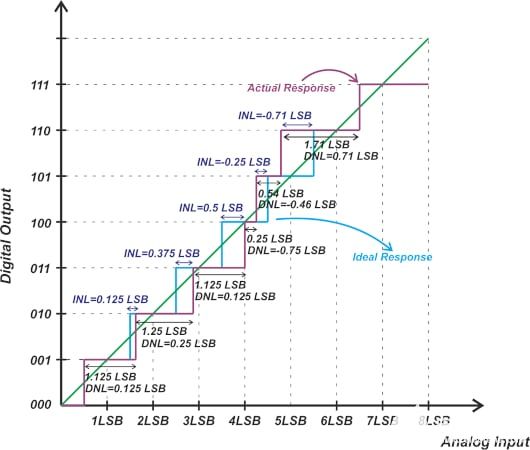
圖1.箭頭 A 的尖端和箭頭 B 的尖端之間的距離是 INL 誤差的度量。

在上圖中，理想的傳遞函數繪制為直線。在本例中，包括INL誤差的非理想傳遞曲線繪制為二階函數Y[n] = k[X[n]]^2。實際上，非理想傳遞函數還可以包含二階、三階、四階等，分量 Y[n] = kX1[n] + k2X[n]^2 + k3X[n]^3 + k4X[n]^4 + ...

對于以下分析，僅考慮二階分量。

X1[n] = sin（2π × fo × nT） fo = 1Hz（為清楚起見，將fo分開），振幅A=1，無相位

Y1[n] = kX1[n]X1[n] 為簡單起見，在本例中設置常量 k = 1

Y1[n] = sin（2π × 1 × nT）sin（2π × 1 × nT）

注意：從三角恒等式中回想一下，Sin（A）Sin（B） = Cos（A-B）/2 - Cos（A+B）/2

Y1[n] = cos（2π × 1 × nT - 2π × 1 × nT）/2 - cos（2π × 1 × nT + 2π × 1 × nT）/2

Y1[n] = cos（0）/2 - cos（4π × 1 × nT）/2

Y1[n] = 1/2 - cos（2π × 2 × nT）/2 （fo = 2Hz 且峰值振幅為 -0.5 的余弦波）

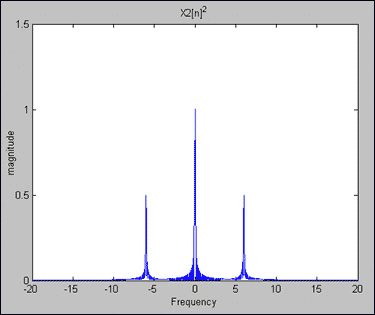
圖2.Y2[n] = X2[n]2= 1/2 - cos（2π × 6 × nT）/2.

X2[n] = sin（2π × fo × nT），fo = 3Hz，振幅 A=1

Y2[n] = sin（2π × 3 × nT）sin（2π × 3 × nT）

Y2[n] = cos（2π × 3 × nT - 2π × 3 × nT）/2 - cos（2π × 3 × nT + 2π × 3 × nT）/2

Y2[n] = cos（0）/2 - cos（4π × 3 × nT）/2

Y2[n] = 1/2 - cos（2π × 6 × nT）/2 （fo = 6Hz 且峰值振幅為 -0.5 的余弦波）

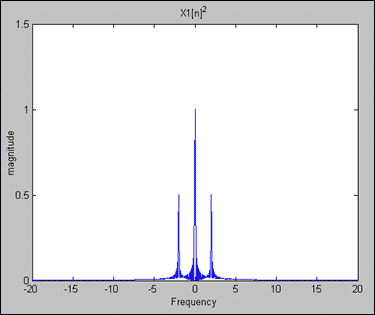
圖3.Y1[n] = X1[n]2= 1/2 - cos（2π × 2 × nT）/2.

我們現在可以應用 X3[n] = X1[n] + X2[n] ，其中 Y3[n] = [X[3]]^2

Y3[n] = [ X1[n] + X2[n] ]^2

Y3[n] = X1[n]X1[n] + 2 X1[n]X2[n] + X2[n]X2[n]

如前所述：

X1[n]X1[n] 導致恒定值為 1/2，余弦波為 2Hz，振幅為 -0.5

X2[n]X2[n] 導致恒定值為 1/2，余弦波為 6Hz，振幅為 -0.5

For 2X1[n]X2[n] = 2sin(2π × 1 × nT)sin(2π × 3 × nT)
                = cos(2π × 1 × nT - 2π × 3 × nT) - cos(2π × 1 × nT + 2π × 3 × nT)
                = cos(-4π × nT) - cos(8π × nT)
                = cos(-2π × 2 × nT) - cos(2π × 4 × nT)
                = cos(2π × 2 × nT) - cos(2π × 4 × nT)    (cosine waves of 2Hz and 4Hz)

因此

For Y3[n]   = X1[n]^2 + X2[n]^2
            = Y1[n] + Y2[n]
            = 1 - cos(2π × 2 × nT)/2  - cos(2π × 6 × nT)/2

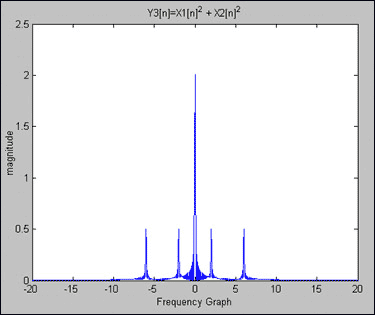
圖4.Y3[n] = X1[n]^2 = 1 - cos（2π × 2 × nT）/2 - cos（2π × 6 × nT）/2.

然而

For Y3[n]   = ( X1[n] + X2[n] )^2
            = 1 - cos(2π × 2 × nT)/2 - cos(2π × 6 × nT)/2 + cos(2π × 2 × nT) - cos(2π × 4 × nT)

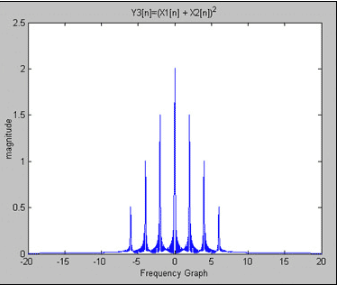
圖5.Y3[n] = X1[n] + X2[n]）^2 = 1 - cos（2π × 2 × nT）/2 - cos（2π × 6 × nT）/2 + cos（2π × 4 × nT）。

由于積分非線性誤差，我們增加了兩個額外的2Hz和4Hz余弦波。不滿足疊加原理，因此該系統是非線性的，不是線性時不變系統。如上所述，需要應用濾波來抑制額外的無用頻率（或旁瓣），從而增加了設計的復雜性和成本。