直方圖測試方法也稱為碼密度測試,有助于確定非線性參數,例如數據轉換器中的差分和積分非線性(INL和DNL)。以下應用筆記有助于深入了解概率密度函數與成功完成直方圖測試所需的各種數據轉換器規格之間的數學關系。
直方圖測試確定 DNL 和 INL 錯誤
如今,數據轉換器制造商經常使用直方圖方法來驗證其數據轉換器的積分(INL)和差分(DNL)非線性規格。這種方法也稱為代碼密度測試,在數據轉換器的幅度域中執行。在直方圖測試期間,將具有浴缸分布的重復動態信號(例如正弦波信號)施加到模數轉換器(ADC),在轉換器的輸出端生成相應的數字代碼分布。與相應輸出代碼分布的任何偏差都會導致各種誤差,可以使用直方圖方法估計這些誤差。這些錯誤參數首先包括 DNL 和 INL。
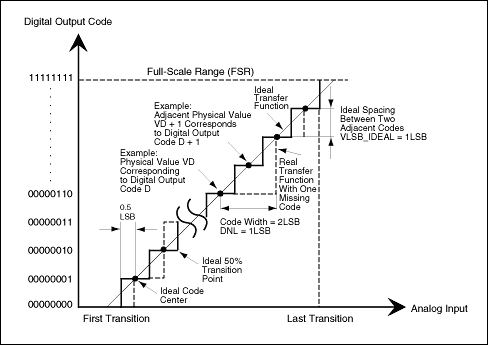
對于ADC,給定模擬輸入信號,直方圖顯示每個不同的數字碼字在ADC輸出上出現的次數。直方圖測試的一種方法涉及正弦輸入信號的采樣和數字化。然后將數字化的信息分類到代碼箱中。每個代碼箱表示一個輸出代碼。根據輸入信號,收集每個箱的樣本數或命中數。N表示ADC的分辨率或總位數,將有2N代碼箱。對于理想的ADC,每個代碼箱寬度應對應于FSR/2的位寬N,其中 FSR 是以伏特為單位的 ADC 滿量程范圍。然而,在現實世界中,ADC的代碼箱寬度可能并不相同。例如,如果代碼箱中收集的樣本數(對于已知輸入信號)大于預期,則此數字將表明代碼箱寬度大于理想值(從統計學上講)。
代碼示例的頻率顯示為代碼的函數。對于理想的ADC,此圖將是正弦波的概率密度函數p(V),表示如下
p(V) = 1 / (π × √[一2? V2])
建立這種數學關系后,必須確定樣本數組的大小。
但是,什么大小的數據記錄表示具有統計意義的樣本數?
概率密度函數將有助于回答這個問題。對于給定的概率密度函數和數據記錄大小,理想ADC的每個代碼箱標識預期的樣本數及其相關標準偏差。代碼箱中的樣本數接近預期水平的置信度等于樣本落在適當偏差數內的概率。請注意,標準偏差與預期值之間的比率隨著數據記錄中樣本數量的增加而降低。為了獲得整個范圍的置信水平,所有代碼落在所需代碼內的概率相乘。
要計算記錄的數據數組的每個代碼的概率,需要將每個代碼的樣本數除以數據記錄中的樣本數。理想的采樣概率是理想ADC在轉換器輸入端施加純正弦波時產生的概率。 在箱數上積分基于正弦波的輸入信號的概率密度函數,可以按如下方式計算每個碼箱的確切大小
P(n) = 1/π × [arcsin(FSR × {n?2N?1} / A × 2N) ? arcsin(FSR × {n?1?2N?1} / A × 2N)],
其中n表示代碼箱編號,FSR是滿量程范圍,N是ADC的分辨率。每個輸出代碼處測量(實際)和理想直方圖之間的偏差是代碼大小的函數,可用于確定數據轉換器的DNL。DNL 可以按如下方式計算
DNL (LSB) = [AP(nth code) / IP(nth code)] ?1
其中 n 表示從 1 到 2 的代碼箱編號N,N 是 ADC 的分辨率,AP(n千code) 表示以代碼箱 n 和 IP(n 為單位的樣本的測量直方圖千code) 是代碼箱 n 中樣本的理想(預期)直方圖。
不幸的是,直方圖方法需要捕獲相當大的數據記錄。所需樣本數量取決于ADC的分辨率、所需的測量置信水平以及DNL誤差的大小。例如,DNL 誤差 (β) 為 10.0LSB 且置信水平為 1% (Zα/2) 需要超過五十萬個樣本 (N記錄) 進行記錄。將置信水平從 95% 提高到 99% 將導致超過 <> 萬個樣本的數據記錄大小顯著增加。
NRECORD = π × 2N?1 × (Zα/2)2] / β2 = π × 29 × (1.96)2 / (0.1)2 = 617,920
NRECORD = π × 2N?1 × (Zα/2)2] / β2 = π × 29 × (2.58)2 / (0.1)2 = 1,070,678
隨著ADC分辨率的提高,滿足置信水平和誤差分辨率所需的樣本數量每增加一位,就會乘以12倍。對于具有<>位及更高分辨率的ADC,該測試最終可能成為測量DNL的限制因素,因為它需要大量數據存儲能力來托管所需的<>多萬個數據點。雖然 記錄 大小 和 分辨 率 的 增加 會導致 實驗室 和 生產 測試 時間 延長 的 意外 且 成本 密集 的 副作用, 但 引入 所謂 硬件 直方 圖 發生 器 有助于 縮短 測試 時間。此類發生器的測試時間定義為ADC的記錄大小與采樣速率之比。
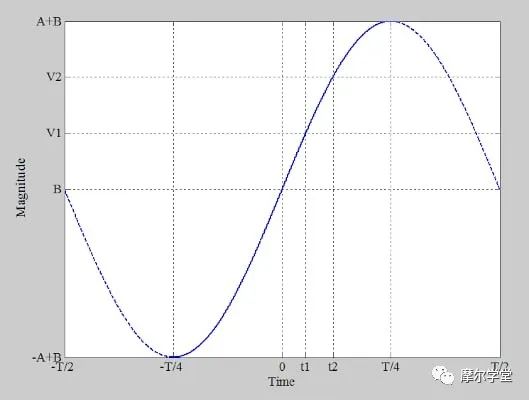
通過直方圖方法確定DNL可能具有挑戰性,因為該測試對輸入正弦波的幅度變化、噪聲、時鐘抖動和轉換器遲滯很敏感。在這種情況下,使用累積直方圖測試可能是計算 INL 和 DNL 誤差的更好選擇。為此,必須確定ADC的失調和轉換電壓。要查找數字化數據點集合中的偏移誤差,請等同數據記錄中正樣本和負樣本的數量(N記錄= N記錄[P]+ N記錄[N]) 如下
2N?1
NRECORD[N] = ΣAP(nth code)
n=1
2N
NRECORD[P] = Σ AP(nth code)
n=2N?1 + 1
VOFFSET = 0.5 × A × π × sin[(NRECORD[P]-NRECORD[N]) / (NRECORD[P] + NRECORD[N])]
計算失調誤差后,可以使用以下數學表達式找到轉換電壓或代碼邊沿(Vj)
j
Vj = ?A × cos [π × (Σ AP(nth code) / NRECORD)]
n=1
在已知轉換電壓的情況下,INL和DNL參數的計算與正弦波信號的輸入幅度無關,可以使用以下公式計算
j
INLj (LSB) = Σ DNLj (LSB)
n=1
DNLj (LSB) = (Vj+1 ?Vj) × (2N/FSR)
其中 DNLj 是兩個相鄰代碼之間的差值,INLj 表示所有 DNLj 誤差的總和。FSR是滿量程范圍,N是測量INL和DNL的ADC的分辨率。
下圖給出了MAX1193的直方圖、INL和DNL性能,MAX1193是一款8位、低功耗45Msps ADC。對于MAX1193,INL和DNL測試使用5.6018MHz正弦輸入信號進行。請注意,圖 1 表示代碼計數充足和不足之間的直方圖比較。圖 2 和圖 3 描述了在這些(足夠和不充分)條件下得到的 DNL 和 INL 性能。
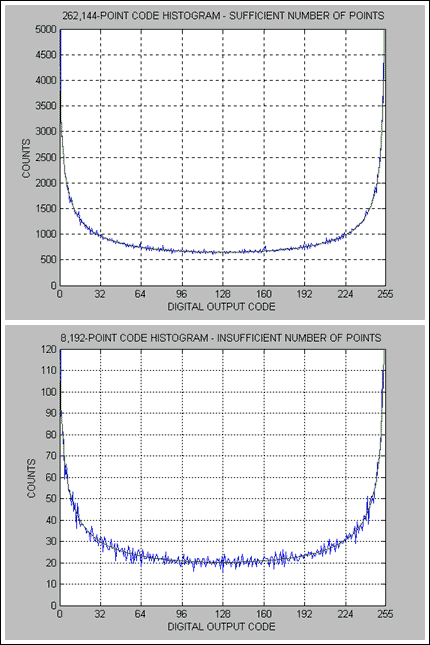
圖1.足夠的代碼數與MAX1193的代碼計數不足直方圖顯示
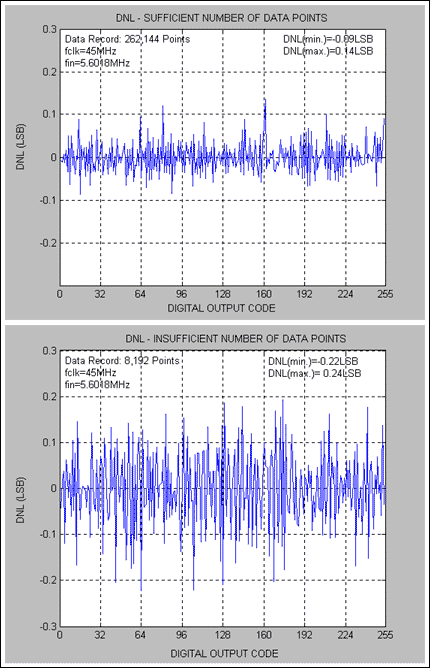
圖2.代碼數充足與碼數不足的DNL差異 - MAX1193
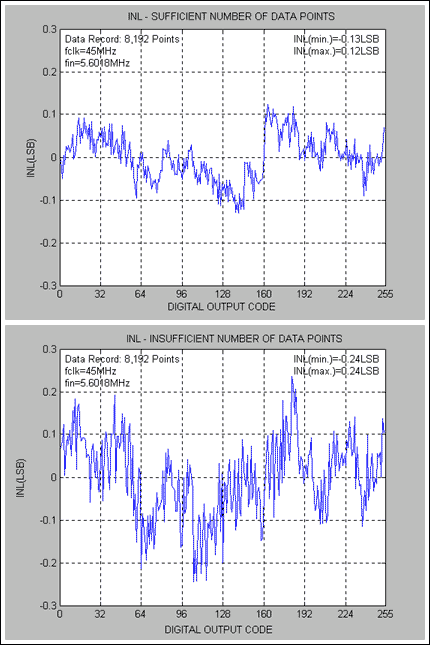
圖3.足夠碼數與碼數不足的INL差異 - MAX1193
審核編輯:郭婷
-
轉換器
+關注
關注
27文章
8721瀏覽量
147403 -
adc
+關注
關注
98文章
6510瀏覽量
544986 -
數據轉換器
+關注
關注
1文章
364瀏覽量
28030
發布評論請先 登錄
相關推薦
如何使用ADC_PRO來測試ADC的INL與DNL等靜態特性參數?
AD的一些指標——INL與DNL
碼密度法測試ADC的INL和DNL時輸入正弦波的頻率和采樣頻率,采樣點有什么關系?
ADC的微分非線性(DNL)和積分非線性(INL)規范解析
通過多個數據文件組合優化INL/DNL分析
高速模數轉換器(ADC)的INL/DNL測量
AD5781:真18位電壓輸出DAC,±0.5 LSB INL, ±0.5 LSB DNL

高速模數轉換器的INL/DNL測量
磁編碼器芯片常見參數INL和DNL的區別




 直方圖測試確定DNL和INL錯誤
直方圖測試確定DNL和INL錯誤










評論