2.1 PID算法數學推導過程
2.1.1 連續系統的PID算法

2.1.2 PID算法的離散化

2.2 位置型PID算法
2.2.1 MATLAB算法
clc
clear
%PID初始化
len = 500 ; %運算次數
y = zeros(1,len); %期望值
y_d = zeros(1,len); %過程值
err = zeros(1,len); %誤差值
err_0 = 0 ; %k時刻誤差
err_1 = 0 ; %k-1時刻誤差
y_d_last = 0 ; %k-1時刻輸出
integral = 0; %積分值
Kp = 0.2; %比例系數
Kd = 0.2; %微分值
Ki = 0.015 ; %積分值
%運算過程
for k=1:1:len
y(k) = 200 ; %期望輸出
err_0 = y(k)-y_d_last; %計算偏差
integral = integral+err_last; %誤差累計
y_d_last = Kp* err_0 + Ki*integral + Kd*( err_1- err_0); %位置型PID運算公式
err_1 = err_0 ;
%更新參數
y_d(k) = y_d_last ;
err(k) = err_1 ;
end
%輸出圖像繪制
t = 1:1:len;
subplot( 2, 1, 1 ) ;
plot( t, y, 'r', t, y_d, 'b' );
axis([0 len, 0 1.5*y(1)])
title('輸出曲線');
xlabel('t')
ylabel('y(t)')
%誤差圖像繪制
subplot( 2, 1, 2 ) ;
plot( t, err );
axis([0 len, 0 1.5*y(1)])
title('誤差曲線');
xlabel('t')
ylabel('e(t)')
MATLAB運行結果如下圖所示。

2.2.2 C算法
#include
struct _pid
{
float SetSpeed ; //設置速度
float ActualSpeed ; //實際速度
float err ; //誤差
float err_last ; //最終誤差
float Kp , Kd , Ki ; //比例系數
float voltage ; //輸出電壓
float integral ; //積分值
}pid;
void PID_Init()
{
pid.SetSpeed = 0 ;
pid.ActualSpeed = 0.0 ;
pid.err = 0.0 ;
pid.err_last = 0.0 ;
pid.voltage = 0.0 ;
pid.integral = 0.0 ;
pid.Kp = 0.2 ;
pid.Kd = 0.2 ;
pid.Ki = 0.015 ;
}
float PID_Realize( float Speed )
{
pid.SetSpeed = Speed ;
pid.err = pid.SetSpeed-pid.ActualSpeed ;
pid.integral += pid.err ;
pid.voltage = pid.Kp*pid.err+pid.Ki*pid.integral+pid.Kd*( pid.err-pid.err_last ) ;
pid.err_last = pid.err ;
pid.ActualSpeed = pid.voltage*1.0 ;
return pid.ActualSpeed ;
}
void main()
{
int count ;
count = 0 ;
PID_Init() ;
while( count<850 )
{
float Speed = PID_Realize( 200.0 ) ;
count ++ ;
}
}
2.3 增量型PID算法
2.3.1 MATLAB算法
clc
clear
%PID初始化
len = 400 ; %運算次數
y = zeros(1,len); %期望值
y_d = zeros(1,len); %過程值
err = zeros(1,len); %誤差值
err_0 = 0 ; %k時刻誤差
err_1 = 0 ; %k-1時刻誤差
err_2 = 0 ; %k-2時刻誤差
y_d_last = 0 ; %k-1時刻輸出
increment = 0 ; %增量
Kp = 0.2; %比例系數
Kd = 0.2; %微分值
Ki = 0.015 ; %積分值
%運算過程
for k=1:1:len
y(k) = 200 ; %期望輸出
err_0 = y(k)-y_d_last; %計算偏差
increment = Kp*(err_0-err_1) + Ki*err_0 + Kd*(err_0-2*err_1+err_2);%增量型PID運算公式
err_2 = err_1;
err_1 = err_0;
y_d_last = y_d_last + increment ; %輸出疊加
%更新參數
y_d(k) = y_d_last ;
err(k) = err_2;
end
%輸出圖像繪制
t = 1:1:len;
subplot( 2, 1, 1 ) ;
plot( t, y, 'r', t, y_d, 'b' );
axis([0 len, 0 1.5*y(1)])
title('輸出曲線');
xlabel('t')
ylabel('y(t)')
%誤差圖像繪制
subplot( 2, 1, 2 ) ;
plot( t, err );
axis([0 len, 0 1.5*y(1)])
title('誤差曲線');
xlabel('t')
ylabel('e(t)')
MATLAB運行結果如下圖所示。

2.3.2 C算法
#include
struct _pid
{
float SetSpeed ; //設置速度
float ActualSpeed ; //實際速度
float err ; //誤差
float err_next ; //上一次誤差
float err_last ; //最終誤差
float Kp , Kd , Ki ; //比例系數
}pid;
void PID_Init()
{
pid.SetSpeed = 0 ;
pid.ActualSpeed = 0.0 ;
pid.err = 0.0 ;
pid.err_last = 0.0 ;
pid.err_next = 0.0 ;
pid.Kp = 0.2 ;
pid.Kd = 0.2 ;
pid.Ki = 0.015 ;
}
float PID_Realize( float Speed )
{
float incrementSpeed ;
pid.SetSpeed = Speed ;
pid.err = pid.SetSpeed-pid.ActualSpeed ;
incrementSpeed=
pid.Kp*(pid.err-pid.err_next)+pid.Ki*pid.err+pid.Kd*( pid.err-2*pid.err_next+pid.err_last ) ;
pid.err_last = pid.err_next ;
pid.err_next = pid.err ;
pid.ActualSpeed += incrementSpeed ;
return pid.ActualSpeed ;
}
void main()
{
int count ;
count = 0 ;
PID_Init() ;
while( count<850 )
{
float Speed = PID_Realize( 200.0 ) ;
count ++ ;
}
}
2.4 積分分離型PID算法
2.4.1 實現原理
為了消除系統的穩態誤差,提高控制精度引入了積分環節,但是在啟動,結束和大幅度增減設定時,短時間內系統輸出有很大的偏差,會造成PID運算的積分積累,導致控制量超過執行機構可能允許的最大動作范囲所對應的極限控制量,從而引起較大的超調,甚至震蕩,為了克服這一問題,引入了積分分離的概念,基本思路是“當給定值與反饋值偏差較大時,取消積分的作用,當被控量接近給定值時,引入積分控制”,用于消除穩態誤差,提高系統的精度。
2.4.2 MATLAB算法
clc
clear
%PID初始化
len = 500 ; %運算次數
y = zeros(1,len); %期望值
y_d = zeros(1,len); %過程值
err = zeros(1,len); %誤差值
err_0 = 0 ; %k時刻誤差
err_1 = 0 ; %k-1時刻誤差
y_d_last = 0 ; %k-1時刻輸出
integral = 0; %積分值
Kp = 0.2; %比例系數
Kd = 0.2; %微分值
Ki = 0.015 ; %積分值
max = 400 ; %積分上限
index = 0 ; %積分有效性
%運算過程
for k=1:1:len
y(k) = 200 ; %期望輸出
err_0 = y(k)-y_d_last; %計算偏差
if abs(err_0) <= y(k)
index = 1 ;
integral = integral+err_0; %誤差累計
else
index = 0 ;
end
y_d_last = Kp*err_0 + Ki*index*integral + Kd*(err_1-err_0); %位置型PID運算公式
err_1 = err_0 ;
%更新參數
y_d(k) = y_d_last ;
err(k) = err_1 ;
end
%輸出圖像繪制
t = 1:1:len;
subplot( 2, 1, 1 ) ;
plot( t, y, 'r', t, y_d, 'b' );
axis([0 len, 0 1.5*y(1)])
title('輸出曲線');
xlabel('t')
ylabel('y(t)')
%誤差圖像繪制
subplot( 2, 1, 2 ) ;
plot( t, err );
axis([0 len, 0 1.5*y(1)])
title('誤差曲線');
xlabel('t')
ylabel('e(t)')
MATLAB運行結果如下圖所示。

2.4.3 C算法
#include
#include
struct _pid
{
float SetSpeed ; //設置速度
float ActualSpeed ; //實際速度
float err ; //誤差
float err_last ; //最終誤差
float Kp , Kd , Ki ; //比例系數
float voltage ; //輸出電壓
float integral ; //積分值
float umax ; //積分上限
float umin ; //積分下限
}pid;
void PID_Init()
{
pid.SetSpeed = 0 ;
pid.ActualSpeed = 0.0 ;
pid.err = 0.0 ;
pid.err_last = 0.0 ;
pid.voltage = 0.0 ;
pid.integral = 0.0 ;
pid.Kp = 0.2 ;
pid.Kd = 0.2 ;
pid.Ki = 0.1 ;
pid.umax = 400 ;
pid.umin = -200 ;
}
float PID_Realize( float Speed )
{
char index ;
pid.SetSpeed = Speed ;
pid.err = pid.SetSpeed-pid.ActualSpeed ;
if( abs(pid.err)<= pid.umax )
{
index = 1 ;
pid.integral += pid.err ;
}
else
index = 0 ;
pid.voltage = pid.Kp*pid.err+index*pid.Ki*pid.integral+pid.Kd*( pid.err-pid.err_last ) ;
pid.err_last = pid.err ;
pid.ActualSpeed = pid.voltage*1.0 ;
return pid.ActualSpeed ;
}
void main()
{
int count ;
count = 0 ;
PID_Init() ;
while( count<1000 )
{
float Speed = PID_Realize( 200.0 ) ;
count ++ ;
printf( "%.2f\\n" , Speed ) ;
}
}
2.5 抗積分飽和型PID算法
2.5.1 實現原理
所謂積分飽和現象是指如果系統存在一個方向的偏差,PID控制器的輸出會因為存在積分環節而不斷累積增大,從而導致執行機構達到極限位置,若控制器輸出響應繼續增大,執行器開度不可能再增大,此時計算機輸出控制量超出了正常運行范圍而進入飽和區,一旦系統出現反向偏差,輸出響應逐漸從飽和區退出,進入飽和區時間越長則退出飽和區的時間也就隨之增加,這段時間里,執行機構仍然停留在極限位置而不能隨著偏差方向立即作出相應的改變,造成控制性能惡化,這種現象稱為積分飽和現象或積分失控現象。實現抗積分飽和算法的基本思路是計算系統的響應時,首先判斷上一時刻的控制量是否超出了極限范圍,如果超過上限,則只累計反向偏差,若低于下限,則只累計正向偏差,從而避免控制量長時間停留在飽和區。
2.5.2 MATLAB算法
clc
clear
%PID初始化
len = 180 ; %運算次數
y = zeros(1,len); %期望值
y_d = zeros(1,len); %過程值
err = zeros(1,len); %誤差值
err_0 = 0 ; %k時刻誤差
err_1 = 0 ; %k-1時刻誤差
y_d_last = 0 ; %k-1時刻輸出
integral = 0; %積分值
Kp = 0.2; %比例系數
Kd = 0.2; %微分值
Ki = 0.1 ; %積分值
max = 400 ; %積分上限
min = -200 ; %積分下限
index = 0 ; %積分有效性
%運算過程
for k=1:1:len
y(k) = 200 ; %期望輸出
err_0 = y(k)-y_d_last; %計算偏差
if y_d_last>max
if abs(err_0) <= y(k)
index = 1 ;
if err_0 < 0
integral = integral+err_0; %誤差累計
end
else
index = 0 ;
end
elseif y_d_last<min
if abs(err_0) <= y(k)
index = 1 ;
if err_0 > 0
integral = integral+err_0; %誤差累計
end
else
index = 0 ;
end
else
if abs(err_0) <= y(k)
index = 1 ;
integral = integral+err_0; %誤差累計
else
index = 0 ;
end
end
y_d_last = Kp*err_0 + Ki*index*integral + Kd*(err_1-err_0); %位置型PID運算公式
err_1 = err_0 ;
%更新參數
y_d(k) = y_d_last ;
err(k) = err_1 ;
end
%輸出圖像繪制
t = 1:1:len;
subplot( 2, 1, 1 ) ;
plot( t, y, 'r', t, y_d, 'b' );
axis([0 len, 0 1.5*y(1)])
title('輸出曲線');
xlabel('t')
ylabel('y(t)')
%誤差圖像繪制
subplot( 2, 1, 2 ) ;
plot( t, err );
axis([0 len, 0 1.5*y(1)])
title('誤差曲線');
xlabel('t')
ylabel('e(t)')
MATLAB運行結果如下圖所示。

2.5.3 C算法
#include
#include
struct _pid
{
float SetSpeed ; //設置速度
float ActualSpeed ; //實際速度
float err ; //誤差
float err_last ; //最終誤差
float Kp , Kd , Ki ; //比例系數
float voltage ; //輸出電壓
float integral ; //積分值
float umax ; //積分上限
float umin ; //積分下限
}pid;
void PID_Init()
{
pid.SetSpeed = 0 ;
pid.ActualSpeed = 0.0 ;
pid.err = 0.0 ;
pid.err_last = 0.0 ;
pid.voltage = 0.0 ;
pid.integral = 0.0 ;
pid.Kp = 0.2 ;
pid.Kd = 0.2 ;
pid.Ki = 0.1 ;
pid.umax = 400 ;
pid.umin = -200 ;
}
float PID_Realize( float Speed )
{
char index ;
pid.SetSpeed = Speed ;
pid.err = pid.SetSpeed-pid.ActualSpeed ;
if( pid.ActualSpeed>pid.umax )
{
if( abs(pid.err)<=200 )
{
index = 1 ;
if( pid.err<0 )
pid.integral += pid.err ;
}
else
index = 0 ;
}
else if( pid.ActualSpeed
2.6 梯形積分PID算法
2.6.1 實現原理
根據梯形算法的積分環節公式

作為PID控制的積分項,其作用是消除余差,為了盡量減小余差,應提高積分項運算精度,為此可以將矩形積分改為梯形積分,具體實現的語句為pid.voltage = pid.Kppid.err+indexpid.Ki pid.integral/2+pid.Kd ( pid.err-pid.err_last ) ;
2.6.2 MATLAB算法
clc
clear
%PID初始化
len = 358 ; %運算次數
y = zeros(1,len); %期望值
y_d = zeros(1,len); %過程值
err = zeros(1,len); %誤差值
err_0 = 0 ; %k時刻誤差
err_1 = 0 ; %k-1時刻誤差
y_d_last = 0 ; %k-1時刻輸出
integral = 0; %積分值
Kp = 0.2; %比例系數
Kd = 0.2; %微分值
Ki = 0.1 ; %積分值
max = 400 ; %積分上限
min = -200 ; %積分下限
index = 0 ; %積分有效性
%運算過程
for k=1:1:len
y(k) = 200 ; %期望輸出
err_0 = y(k)-y_d_last; %計算偏差
if y_d_last>max
if abs(err_0) <= y(k)
index = 1 ;
if err_0 < 0
integral = integral+err_0; %誤差累計
end
else
index = 0 ;
end
elseif y_d_last<min
if abs(err_0) <= y(k)
index = 1 ;
if err_0 > 0
integral = integral+err_0; %誤差累計
end
else
index = 0 ;
end
else
if abs(err_0) <= y(k)
index = 1 ;
integral = integral+err_0; %誤差累計
else
index = 0 ;
end
end
y_d_last = Kp*err_0 + Ki*index*integral/2 + Kd*(err_1-err_0); %PID運算公式
err_1 = err_0 ;
%更新參數
y_d(k) = y_d_last ;
err(k) = err_1 ;
end
%輸出圖像繪制
t = 1:1:len;
subplot( 2, 1, 1 ) ;
plot( t, y, 'r', t, y_d, 'b' );
axis([0 len, 0 1.5*y(1)])
title('輸出曲線');
xlabel('t')
ylabel('y(t)')
%誤差圖像繪制
subplot( 2, 1, 2 ) ;
plot( t, err );
axis([0 len, 0 1.5*y(1)])
title('誤差曲線');
xlabel('t')
ylabel('e(t)')
MATLAB運行結果如下圖所示。

2.6.3 C算法
#include
#include
struct _pid
{
float SetSpeed ; //設置速度
float ActualSpeed ; //實際速度
float err ; //誤差
float err_last ; //最終誤差
float Kp , Kd , Ki ; //比例系數
float voltage ; //輸出電壓
float integral ; //積分值
float umax ; //積分上限
float umin ; //積分下限
}pid;
void PID_Init()
{
pid.SetSpeed = 0 ;
pid.ActualSpeed = 0.0 ;
pid.err = 0.0 ;
pid.err_last = 0.0 ;
pid.voltage = 0.0 ;
pid.integral = 0.0 ;
pid.Kp = 0.2 ;
pid.Kd = 0.2 ;
pid.Ki = 0.1 ;
pid.umax = 400 ;
pid.umin = -200 ;
}
float PID_Realize( float Speed )
{
char index ;
pid.SetSpeed = Speed ;
pid.err = pid.SetSpeed-pid.ActualSpeed ;
if( pid.ActualSpeed>pid.umax )
{
if( abs(pid.err)<=200 )
{
index = 1 ;
if( pid.err<0 )
pid.integral += pid.err ;
}
else
index = 0 ;
}
else if( pid.ActualSpeed
2.7 變積分PID算法
2.7.1 實現原理
變積分PID可以看做是積分分離的PID算法的更一般形式,在普通的PID控制算法中,由于積分系數是常數,所以在整個控制過程中,積分增量是不變的,但是,系統對于積分項的要求是,系統偏差較大時,積分作用應該減弱甚至全無,而在偏差較小時,則應該加強,積分系數取大了會引起超調,甚至積分飽和,取小了又不能短時間內消除靜差,因此,需要根據系統偏差的大小改變積分速度。
變積分PID的基本思想是改變積分項的累加速度,使其與偏差大小相對應,偏差越大,積分越慢,偏差較小,積分越快。
這里給積分系數前加一個比例系數index,使最終的比例環節的積分系數為Ki*index。
2.7.1 MATLAB算法
clc
clear
%PID初始化
len = 200 ; %運算次數
y = zeros(1,len); %期望值
y_d = zeros(1,len); %過程值
err = zeros(1,len); %誤差值
err_0 = 0 ; %k時刻誤差
err_1 = 0 ; %k-1時刻誤差
y_d_last = 0 ; %k-1時刻輸出
integral = 0; %積分值
Kp = 0.4; %比例系數
Kd = 0.2; %微分值
Ki = 0.2 ; %積分值
max = 400 ; %積分上限
min = -200 ; %積分下限
index = 0 ; %積分有效性
%運算過程
for k=1:1:len
y(k) = 200 ; %期望輸出
err_0 = y(k)-y_d_last; %計算偏差
if abs(err_0) > max
index = 0 ;
elseif abs(err_0) < min
index = 1 ;
integral = integral+err_0; %誤差累計
else
index = ( max-abs(err_0) )/20 ;
integral = integral+err_0; %誤差累計
end
y_d_last = Kp*err_0 + Ki*index*integral/2 + Kd*(err_1-err_0); %PID運算公式
err_1 = err_0 ;
%更新參數
y_d(k) = y_d_last ;
err(k) = err_1 ;
end
%輸出圖像繪制
t = 1:1:len;
subplot( 2, 1, 1 ) ;
plot( t, y, 'r', t, y_d, 'b' );
axis([0 len, 0 1.5*y(1)])
title('輸出曲線');
xlabel('t')
ylabel('y(t)')
%誤差圖像繪制
subplot( 2, 1, 2 ) ;
plot( t, err );
axis([0 len, 0 1.5*y(1)])
title('誤差曲線');
xlabel('t')
ylabel('e(t)')
MATLAB運行結果如下圖所示。

2.7.2 C算法
#include
#include
struct _pid
{
float SetSpeed ; //設置速度
float ActualSpeed ; //實際速度
float err ; //誤差
float err_last ; //最終誤差
float Kp , Kd , Ki ; //比例系數
float voltage ; //輸出電壓
float integral ; //積分值
}pid;
void PID_Init()
{
pid.SetSpeed = 0 ;
pid.ActualSpeed = 0.0 ;
pid.err = 0.0 ;
pid.err_last = 0.0 ;
pid.voltage = 0.0 ;
pid.integral = 0.0 ;
pid.Kp = 0.4 ;
pid.Kd = 0.2 ;
pid.Ki = 0.2 ;
}
float PID_Realize( float Speed )
{
char index ;
pid.SetSpeed = Speed ;
pid.err = pid.SetSpeed-pid.ActualSpeed ;
if( abs(pid.err)>200 )
index = 0 ;
else if( abs(pid.err)<180 )
{
index = 1 ;
pid.integral += pid.err ;
}
else
{
index = ( 200-abs(pid.err) )/20 ;
pid.integral += pid.err ;
}
pid.voltage = pid.Kp*pid.err+index*pid.Ki*pid.integral/2+pid.Kd*( pid.err-pid.err_last ) ;
pid.err_last = pid.err ;
pid.ActualSpeed = pid.voltage*1.0 ;
return pid.ActualSpeed ;
}
void main()
{
int count ;
count = 0 ;
PID_Init() ;
while( count<150 )
{
float Speed = PID_Realize( 200.0 ) ;
count ++ ;
printf( "%.2f\\n" , Speed ) ;
}
}
2.8 專家PID與模糊PID算法思想
PID的控制思想非常簡單,主要就是比例,積分和微分環節的參數整定過程,對于執行期控制模型確定或者控制模型簡單的系統來說,參數的整定可以通過計算獲得,對于一般精度要求不是很高的執行器系統,可以采用拼湊的方法進行實驗型的整定。
但是,實際的系統大部分屬于非線性系統,或者說是系統模型不確定的系統,如果控制精度要求較高的話,那么對于參數的整定過程也是有難度的,專家PID和模糊PID就是為了滿足這方面的需求而設計的,專家算法和模糊算法都歸屬于智能算法的范疇,智能算法最大的優點就是在控制模型未知的情況下,可以對模型進行控制,這里需要注意的是,專家PID也好,模糊PID也好,絕對不是專家系統或模糊算大與PID控制算法的簡單加和,它是專家系統或者模糊算法在PID控制器參數整定上的應用,也就是說,智能算法是輔助PID進行參數整定的手段。
關于專家PID的C語言實現,需要找到一些依據,還需要從PID系數本身考慮。
1、比例系數Kp的作用是加快系統的響應速度,提高系統的調節精度,Kp越大,系統的響應速度越快,調節的精度越高,但是容易產生超調,甚至會引起系統不穩定,Kp取值過小,則會降低系統的調節精度,拖慢響應速度,從而延長調節時間,使系統的靜態,動態特性變差。
2、積分系數Ki的作用是消除系統的穩態誤差,Ki越大,系統的靜態誤差消除得越快,但是若Ki過大,在響應過程的初期就會產生積分飽和的現象,從而引起相應過程的較大超調,若Ki過小,將使系統靜態誤差難以消除,影像系統的調節精度。
3、微分系數Kd的作用是改善系統的動態特性,其作用主要是在響應過程中抑制偏差向任何方向的變化,對偏差變化進行提前預報,但是若Kd過大,會使響應過程提前制動,從而延長調節時間,而且會降低系統的抗干擾性。

2.9 PID算法應用——電機轉速控制
PID是一種廣泛應用在控制理論中的算法,以直流電機為例,要想精確控制電機的轉速就需要形成一種閉環控制思想。首先將一個默認的輸入端的電壓值發送給直流電機,通過轉速傳感器將當前電機的轉速反饋到輸入端,通過與輸入端做運算,如果轉速高于設定的值,則減小輸入端電壓,如果轉速低于設定的值,則提高輸入端電壓,由此形成了一種閉環控制回路,即通過不停的對輸出端進行反饋,以達到精確控制的目的。為了使控制系統的速度更快,精確性更高,穩定性更強,PID控制器被廣泛應用在了這里面,現在我們通過MATLAB的Simulink來實現直流電機的PID控制。

一個直流電機的模型如上圖所示,為了簡化討論,假設轉子和轉軸都是剛體,且轉子受到的磁場恒定,轉子收到的摩擦力與速度成正比,該電機的物理參數為:
(1)轉子的轉動慣量J=0.01kg·m^2^
(2)電機摩擦系數b=0.01N···m·s
(3)電動勢常數Ke=0.01V/rad/sec
(4)電機扭矩常數Kt=0.01N·m/Amp
(5)電阻R=1Ω
(6)電感L=0.5H

我們希望控制器輸入1V電壓的時候穩定狀態下保持0.1rad/sec的轉速,穩定時間2s,穩態誤差低于1%,受到階躍輸入干擾的時候超調小于5%。Matlab的仿真并不像之前學習51的時候用的Protuse一樣,可以看到直觀效果,Matlab的仿真實際是對數學的計算過程,即輸入與輸出必須都抽象成函數表達式進行,通過觀察輸出的函數表達式與波形來判斷系統的工作狀態與性能。我們將上面得到的復頻域下的函數表達式代入參數,得到

通過Simulink創建仿真圖如下圖所示。

雙擊PID控制器的圖標,打開了以下對話框。

對話框內的這三個參數就是PID控制器的三個參數,其中Proportional代表比例環節,Integral代表積分環節,Derivative代表微分環節,通過修改這三個參數達到實現控制系統的目的。
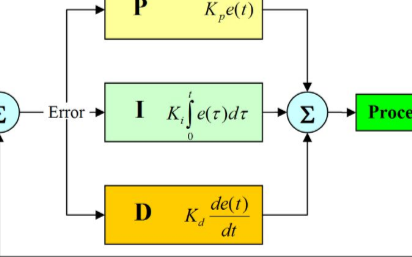
在PID控制中,這三個參數分別對系統控制有以下幾個作用:
(1)比例環節P:控制輸出響應的速度,減小穩態誤差,但是會增大超調量
(2)積分環節I:消除系統的穩態誤差,加快達到穩定所需的時間,但也會增大超調量
(3)微分環節D:加快動態過程,容易引起系統震蕩,同樣,微分環節也會增大超調量
為了滿足:
(1)穩定時間2s
(2)穩態誤差低于1%
(3)超調小于5%
這三個條件,我們首先修改比例環節,用來滿足穩態誤差低于1%這個參數。通過實驗發現,當比例環節設定在100以上的時候,穩態誤差低于1%,如下圖所示。

但是我們發現

即系統的超調量較大,達到了20%,此時需要調節微分環節達到目的,我們通過實驗發現,當微分環節超過10時,系統的超調如下圖所示。

此時系統已經不存在超調,現在只需要解決穩定時間小于2s這個參數即可,我們通過設置積分環節達到這個目的,通過實驗發現,當系統的積分環節大于200時,穩定時間小于2s。此時整個系統的波形如下圖所示。

-
PID
+關注
關注
35文章
1473瀏覽量
85649 -
穩態誤差
+關注
關注
0文章
8瀏覽量
2119 -
系統
+關注
關注
1文章
1018瀏覽量
21381
發布評論請先 登錄
相關推薦




 什么是PID算法
什么是PID算法











評論