作者 |李建文華東師范大學軟件工程學院博導
版塊 |鑒源論壇 · 觀模
01模型檢查的歷史
模型檢查是一種起源于20世紀70年代末的形式化驗證技術。該技術最初由Edmund M. Clarke、E. Allen Emerson和Joseph Sifakis提出,他們因在模型檢查領域的貢獻而獲得了2007年的圖靈獎。模型檢查的提出最初是為了對并發和分布式系統做自動化驗證,這些系統越來越復雜,手動驗證則變得越來越困難。模型檢查涉及系統地探索系統的所有可能狀態,并檢查每個狀態是否滿足某些屬性。
在早期階段,模型檢查可以通過顯示地計算Kripke結構上的不動點(針對CTL描述的性質) [1]或者是在由模型和LTL性質構造的乘積自動機上做狀態搜索 [2]來完成。盡管這些技術非常直觀且易于理解,但它們處理大型系統的能力非常有限,現在它們已經被以BDD [3]和SAT求解器 [4]為計算核心的符號模型檢查技術所取代。事實上,基于SAT求解器的模型檢查技術是目前最有前景的自動化驗證技術。目前最先進的基于SAT求解器的模型檢查技術包括BMC [5],IMC [6],IC3/PDR [7],和CAR [8]。
模型檢查已被應用于各種系統,包括硬件電路、通信協議、操作系統和軟件程序。它已被用于在部署之前檢測系統中的錯誤和缺陷,這可以在開發過程中節省時間和金錢。今天,模型檢查是一個活躍的研究和開發領域,研究人員正在不斷努力,以提高其拓展性、準確性和可用性。
02模型檢查問題描述
模型檢查問題是說:給定一個模型M,或者說一個狀態遷移系統,如何判斷M是否滿足安全性質P。在具體算法實現中,我們往往是從初始狀態I出發,判斷┐P代表的狀態是否可達,即是否所有I可達的狀態都是滿足安全性質P的。如果我們在算法中找到了反例,即從I出發,經過一系列狀態,可以到達┐P,則我們返回反例,用以說明安全性質P不成立;如果我們找到了一個不變式,即證明了從I出發,所有可達的范圍都在一個滿足P的狀態集合中,則我們返回驗證通過,安全性質P成立。下面我們先簡要介紹幾個常見的模型檢查算法。
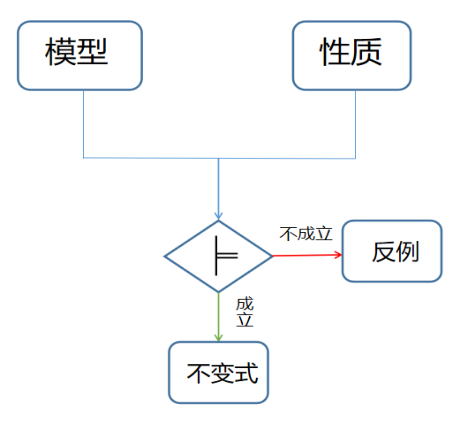
圖1 模型檢查問題示例圖
03模型檢查算法介紹
3.1 Bounded Model Checking (BMC)
BMC是一個簡單但是高效的模型檢查算法,類似于圖搜索中的廣度優先搜索。BMC從初始狀態出發,先判斷是否可以直接一步轉移到┐P,也就是不安全的狀態中,若可以,則找出了一個長度為1的反例;若不行,則說明在初始狀態一步的范圍內,安全性質成立,接著,BMC增大步數,判定從初始狀態出發,是否可以兩步轉移到┐P,同樣地,若可達則返回反例,若不可達,則繼續增大步數,直到找到反例或者達到限定的時間為止。
如下圖所示,從S0出發,先確定一步可達的S1和S2滿足性質,接著增大步數,確定兩步可達的S3滿足性質,再確定三步可達的S4和S5滿足性質,最終步數為4時,檢查出四步可達的S6不滿足性質,從而得到反例。
使用BMC算法可以很快地找到長度最短的反例,但是它的局限性也很大,假設BMC在k步之內找不到反例,這只能說明初始狀態k步可達的狀態滿足安全性質,而不能證明初始狀態可達的狀態都是滿足安全性質的,也就是說,BMC只適用于反例的尋找,而不適合證明模型滿足安全性質。
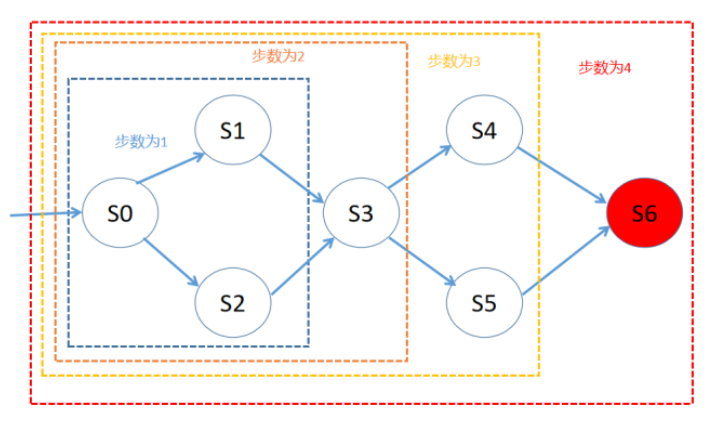
圖2:BMC算法示例圖
3.2 Interpolation Model Checking (IMC)
IMC是在BMC的基礎上改進來的模型檢查算法,它不僅可以查找反例,也可以證明模型是滿足安全性質P的,彌補了BMC算法的缺陷。
簡要地說,在查找反例上,IMC和BMC一樣,都是靠確定從初始狀態出發,┐P代表的非安全狀態是否是k步可達的,如果是,則找到了反例,若不是,則繼續增大k的值。和BMC不同的是,對于每一個步數k,IMC都維持了一個初始狀態k步之內可達的狀態的超集R,即R里面也包含了一些其他的狀態,且R里面的元素都滿足安全性質,在尋找反例的過程中,IMC不斷擴大集合R,若在某個時刻,R不能被擴大,即R里面的元素只能轉移到R里面,則我們找到了一個不變式,即證明了從初始狀態出發,可達的所有狀態都是滿足安全性質的,從而證明了模型是滿足安全性質P的。
如下圖所示,從初始狀態S0出發,我們找到了一個狀態集合R,使得S0可達的狀態S1、S2和S3都在集合R中,且R中的元素都滿足安全性質,因此我們證明了模型是滿足安全性質的,集合R就是證據。
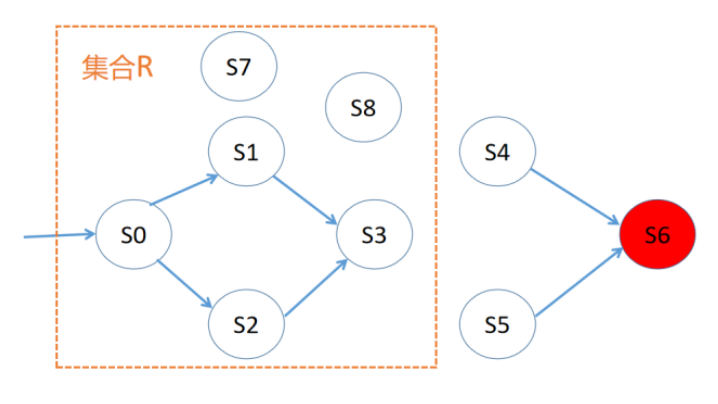
圖3 IMC算法示例圖
3.3 Property Directed Reachability (PDR)
PDR是一個較為復雜的模型檢查算法,簡要地說,它維持了一個滿足安全性質P的狀態集合的序列F,其中F(0)是初始狀態I,而F(1)則是初始狀態一步之內可達的集合的超集,即它里面除了有初始狀態一步之內可達的狀態,也包含了一些其他的狀態,以此類推,后面每一個F(i)集合都是前一個F(i-1)集合的一步之內可達的集合的超集,PDR算法不斷地在F(i)集合中尋找那些可以一步轉移到┐P的元素S,若F(i)中的其他元素可以一步轉移到S,則PDR接著判斷F(i-1)中的元素可不可以兩步轉移到S,以此類推,若在F(0),即初始狀態中,有元素可以多步轉移到S,則找到了一個反例,即性質P不成立,如果在這個過程中,我們找到一個F(i)集合,使得它里面的元素都不能轉移到S,則我們可以把S從這個集合及它之前的集合中刪除,我們不斷重復這個過程,如果在某一步,存在某個F(i)使得F(i)=F(i-1),即F(i-1)里面的狀態只能轉移到F(i-1)里面時,我們就找到了一個不變式,即所有初始狀態可達的狀態都滿足了性質P,證明了性質P成立。
如下圖所示,在集合F(i+1)中,狀態S4可以一步轉移到非安全狀態S6,但是集合F(i+1)中的其他集合不能轉移到S4,因此我們把S4從Fi+1及其之前的集合中刪除,刪除S4后,我們發現集合F(i+1)和F(i)相等,即此時F(i)里面的狀態只能轉移到F(i)里面,因為F(i)是初始狀態可達的狀態的超集,從而初始狀態可達的元素都在F(i)中,因此模型的安全性質就得到了滿足,F(i)就是證據。
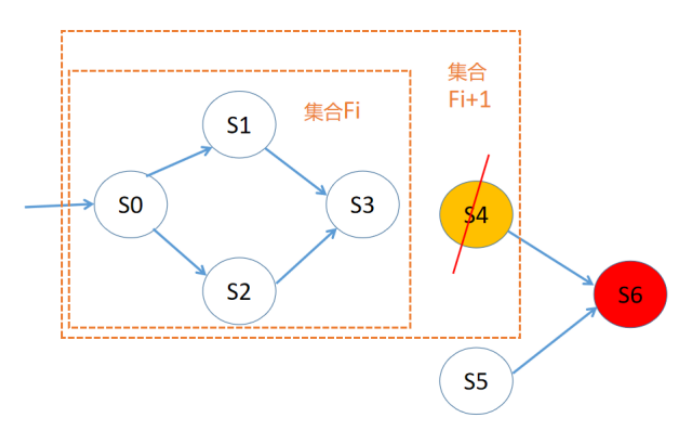
圖4 PDR算法示例圖
3.4 Complementary Approximate Reachability (CAR)
CAR算法也是一個較為復雜的模型檢查算法,可以有兩個搜索方向(Forward CAR和Backward CAR),后續我們以Backward CAR為例。CAR維護了兩個序列,B序列和F序列,F序列是從初始狀態I出發可達的狀態的子集的集合,B序列則是可以到達非安全狀態的!P的狀態的超集的集合,且F(0)= I , B(0)= !P。維護子集與超集的原因是F序列和B序列都是動態的,Fi的元素會隨著算法運行不斷增多,子集會越來越接近原集。而B(i)的元素則會不斷減少,超集也會越來越接近原集。CAR算法就是不斷地去做類似的SAT調用,然后根據結果去更新F和B序列。例如CAR算法會不斷地通過SAT來判斷某個狀態s能否一步轉移到B(i),若成立,則可以拿到s的一個后繼狀態s'并把其加入到F序列,隨后CAR則遞歸詢問s'是否可以轉移到B(i-1);若不成立,CAR則會拿到一個uc(最小不滿足核),并把這個uc來更新B(i+1)。
若存在某個B(i),其是所有B(j) (j < i) 的并集的子集,那么模型是安全的。安全性條件生效表明B序列不會再擴大,即使繼續擴展B序列,新的B(i+1)中的元素,只會是下標更小的B(i)中出現過的元素,這意味著初始狀態I不可能到達B(0),因此模型是安全的。此時從B0至B(i)的并集構成了一個不變式。如果某一個狀態空間F(i)中,存在一個狀態s,此狀態屬于非安全狀態!P,則得到一條以I為起點,狀態s為終點路徑,這條路徑是待驗證性質的反例,將被返回。
如下圖所示,我們發現集合B(i+1)包含在所有B(j) (j < i+1) 的并集中,因此安全性條件生效,B(j) (j < i+1) 的并集就是我們要找的不變式(安全性證明)。
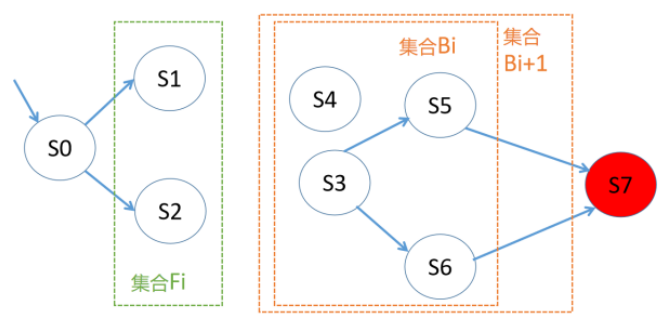
圖5 CAR算法示例圖
參考文獻:
[1] E. Clarke and H. Schlingloff, “Model checking,” in Handbook of Automated Reasoning, A. Robinson and A. Voronkov, Eds. MIT Press, 2001, pp. 1635–1790.
[2] O. Kupferman, N. Piterman, and M. Y. Vardi, “An automata-theoretic approach to infinite-state systems,” in Time for Verification: Essays in Memory of Amir Pnueli, Z. Manna and D. A. Peled, Eds. Berlin, Heidelberg: Springer Berlin Heidelberg, 2010, pp. 202–259.
[3] K. L. McMillan, Symbolic Model Checking. Boston, MA: Springer US, 1993.
[4] Y. Vizel, G. Weissenbacher, and S. Malik, “Boolean satisfiability solvers and their applications in model checking,” Proceedings of the IEEE, vol.103, no. 11, pp. 2021–2035, 2015.
[5] A. Biere, A. Cimatti, E. Clarke, and Y. Zhu, “Symbolic model checking without BDDs,” in Tools and Algorithms for the Construction and Analysis of Systems (TACAS), W. R. Cleaveland, Ed. Berlin, Heidelberg: Springer Berlin Heidelberg, 1999, pp. 193–207.
[6] K. L. McMillan, “Interpolation and SAT-based model checking,” in Computer Aided Verification, W. A. Hunt and F. Somenzi, Eds. Berlin, Heidelberg: Springer Berlin Heidelberg, 2003, pp. 1–13.
[7] A. R. Bradley, “SAT-based model checking without unrolling,” in Verification, Model Checking, and Abstract Interpretation, R. Jhala and D. Schmidt, Eds. Berlin, Heidelberg: Springer Berlin Heidelberg, 2011, pp. 70–87.
[8] J. Li, R. Dureja, G. Pu, K. Y. Rozier, and M. Y. Vardi, “Simplecar: An efficient bug-finding tool based on approximate reachability,” in Computer Aided Verification, H. Chockler and G. Weissenbacher, Eds. Cham: Springer International Publishing, 2018, pp. 37–44.
審核編輯黃宇
-
算法
+關注
關注
23文章
4626瀏覽量
93151 -
PDR
+關注
關注
1文章
7瀏覽量
12384
發布評論請先 登錄
相關推薦
HarmonyOS NEXT應用元服務開發Intents Kit(意圖框架服務)綜述
高效大模型的推理綜述
FSS里面頻率選擇表面模型仿真問題
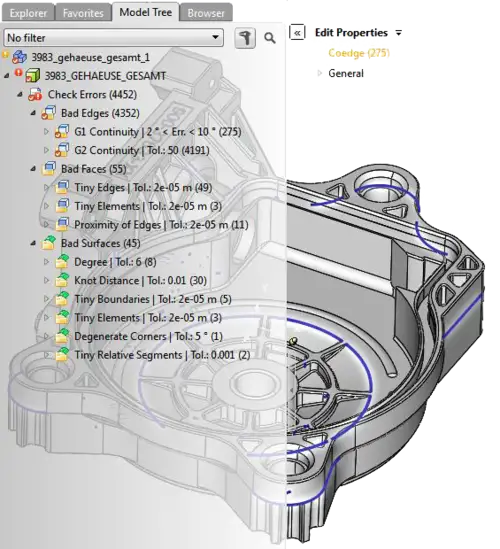
掃描模型前模型檢查的注意事項
電路燈不亮怎么檢查
安寶特產品 安寶特3D Evolution:高效準確的CAD質量檢查工具
快恢復橋檢查方法有哪些?

圖像分割與語義分割中的CNN模型綜述
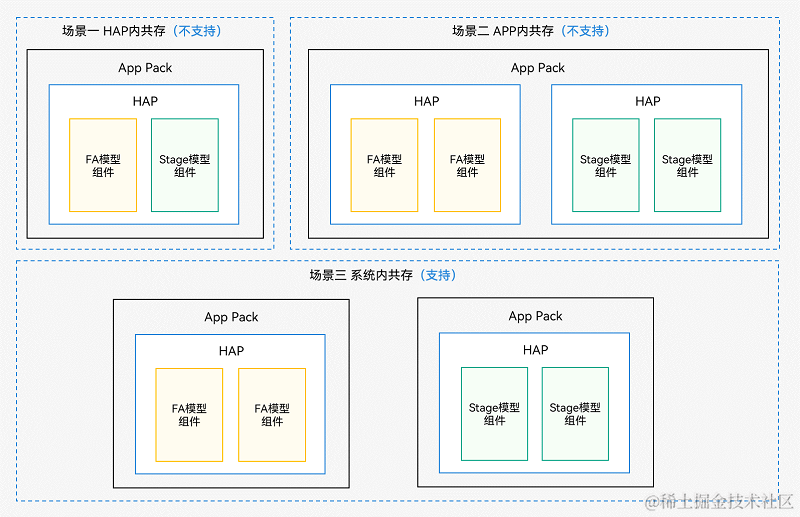
鴻蒙開發Ability Kit程序框架服務:FA模型與Stage模型應用組件互通綜述
電路板檢查故障的六大方法有哪些
【大語言模型:原理與工程實踐】大語言模型的應用
【大語言模型:原理與工程實踐】大語言模型的評測
【大語言模型:原理與工程實踐】核心技術綜述
腦機接口電極界面材料與改性技術進展綜述




 模型檢查綜述
模型檢查綜述











評論