矢量的正交分解
1.矢量正交
兩矢量V1與V2正交,夾角為90°
兩正交矢量的內積為零
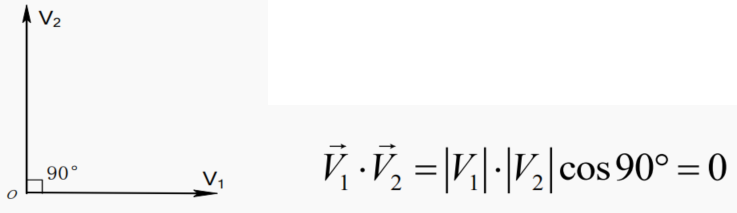
2.正交矢量集:
由兩兩正交的矢量組成的矢量集合
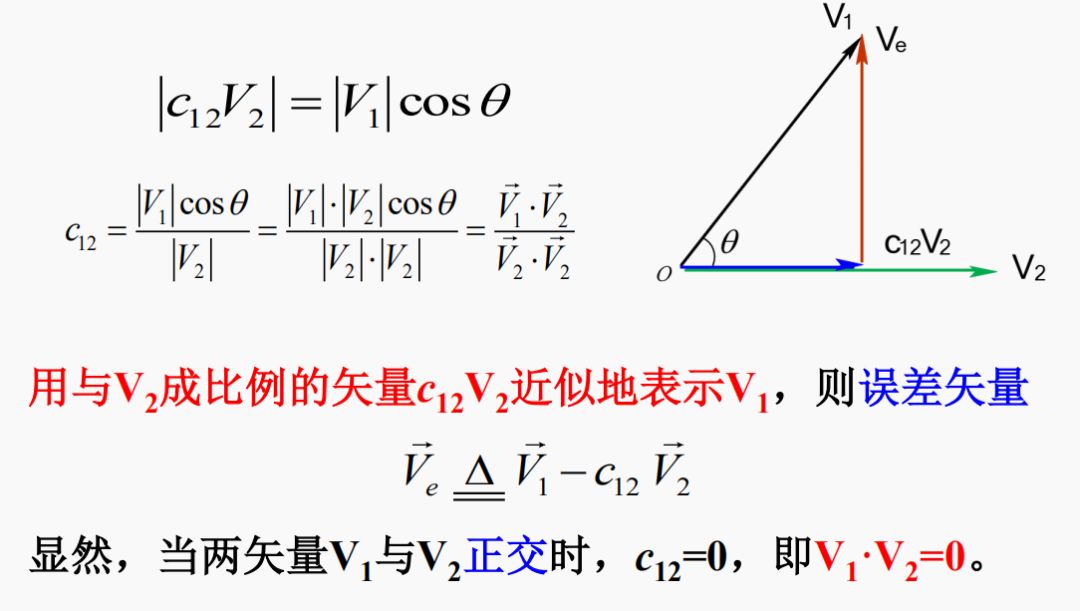
非正交矢量的近似表示及誤差
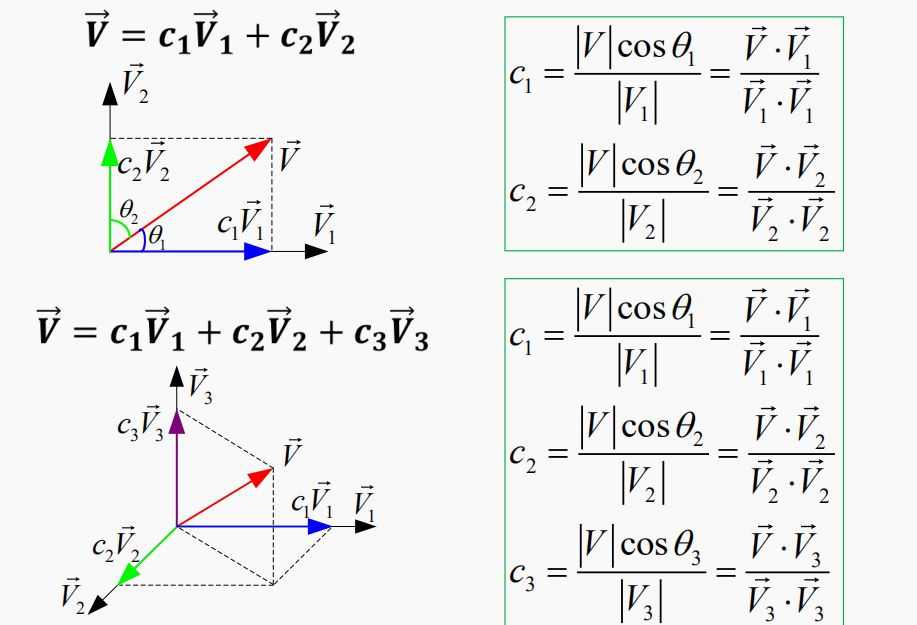
4.矢量正交分解:任意N維矢量可由N維正交坐標系表示
推廣到n維空間:n維空間的任一矢量V,可以精確地表示為n個正交矢量的線性組合, 即
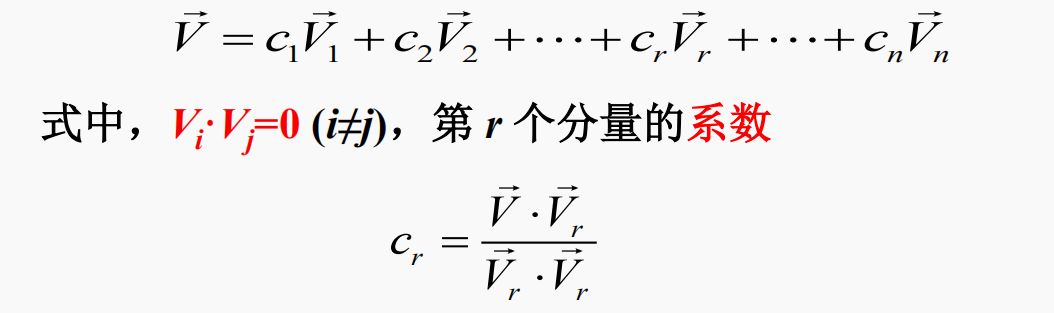
思路:
將矢量空間正交分解的概念可推廣到信號空間:在信號空間找到若干個相互正交的信號作為基本信號,使得信號空間中任意信號均可表示成它們的線性組合。
信號的正交分解
1.信號正交
【定義】

說明:實函數正交

2.正交函數集:

說明:如果 Ki=1,稱為標準正交函數集。
3.完備正交函數集:

例:兩組典型的在區間(t0,t0+T )(T=2π/Ω)上的完備正交函數集
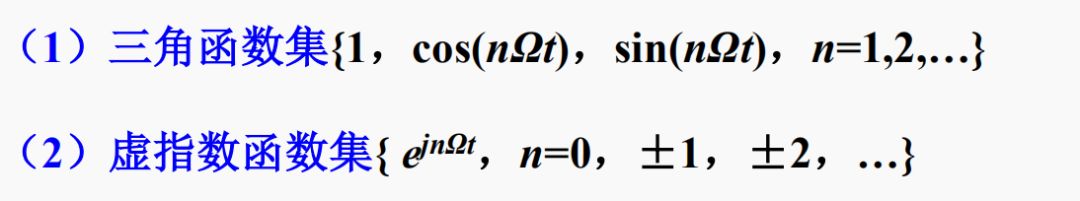
信號的正交分解

如何選擇各系數Cj,使f(t)與近似函數之間誤差在區間(t1,t2)內為最小?
通常使誤差的方均值(稱為均方誤差)最小。
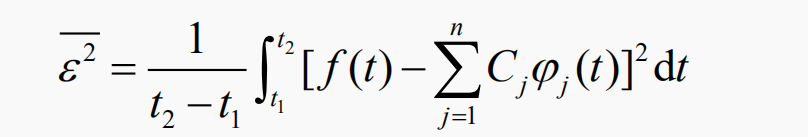
為使上式最小(系數Cj變化時),有
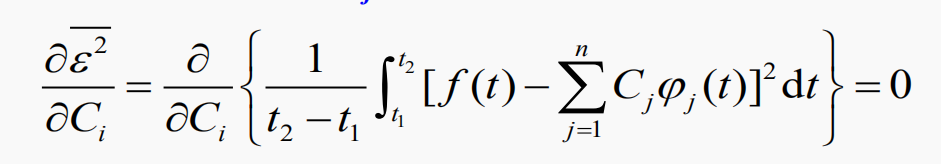
展開被積函數,并求導,只有兩項不為0,寫為:
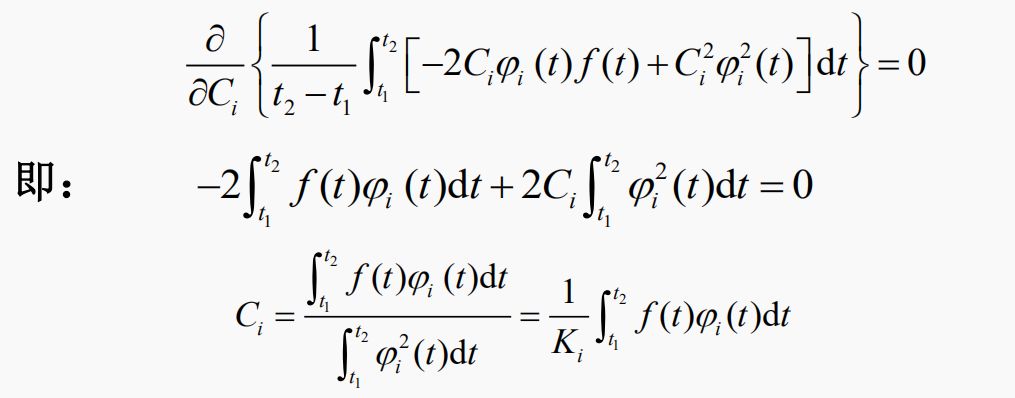
代入,得最小均方誤差
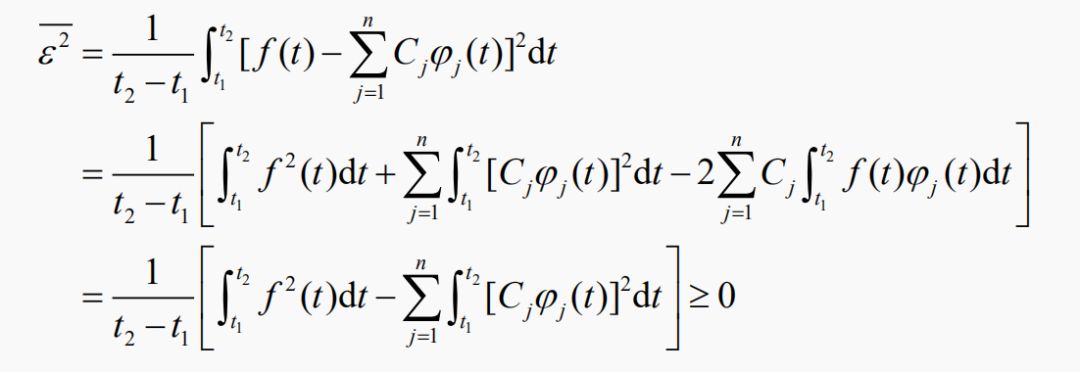
在用正交函數去近似f(t)時,所取的項數越多,即n越大,則均方誤差越小。 當n→∞時(完備正交函數集),均方誤差為零。
結論:
任意信號f(t)可以表示為無窮多個正交函數之和 :
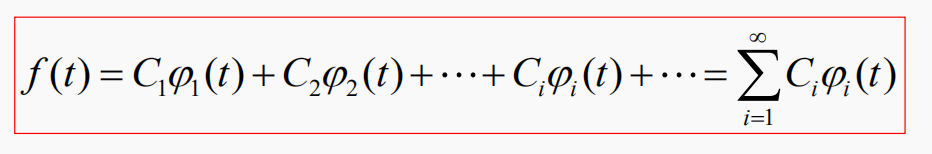
上式稱為信號的正交展開式,也稱為廣義傅里葉級數
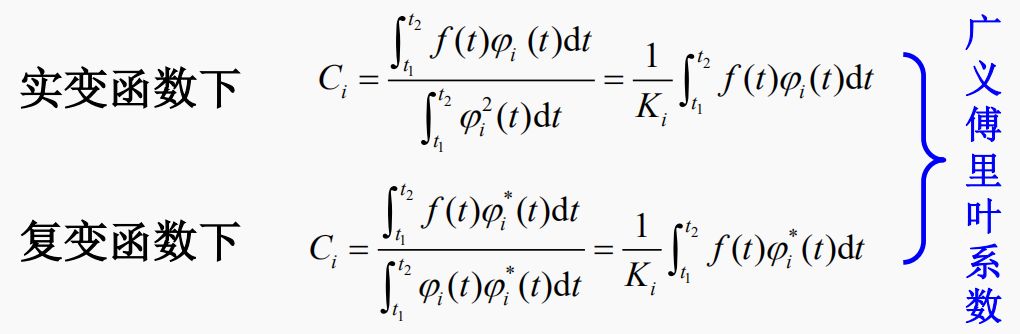
帕斯瓦爾定理
帕斯瓦爾方程:

物理意義:在區間(t1,t2), 信號f(t)所含有的能量恒等于此信號在完備正交函數集中各正交分量能量之和,即能量守恒定理, 也稱帕斯瓦爾定理。
數學本質:矢量空間信號正交變換的范數不變性。
-
信號
+關注
關注
11文章
2797瀏覽量
76935 -
函數
+關注
關注
3文章
4340瀏覽量
62791 -
矢量
+關注
關注
0文章
95瀏覽量
23759 -
正交分解
+關注
關注
0文章
4瀏覽量
7434
發布評論請先 登錄
相關推薦
信號的正交分解和差分傳輸的區別
基于CORDIC技術的無開方無除法的MQR陣分解方法
關鍵基于二維小波變換的圖像矢量分解消噪方法
電磁波正交極化,電磁波正交極化原理是什么?
一種信號矢量分解的采樣濾波移動節點定位算法
非正交三維坐標系下多電平空間矢量調制策略




 詳解矢量的正交分解
詳解矢量的正交分解
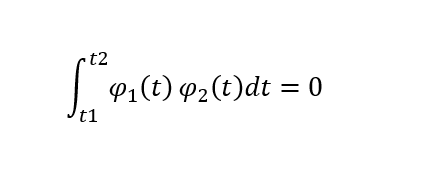










評論