圖深度學習(Graph Deep Learning) 多年來一直在加速發(fā)展。許多現(xiàn)實生活問題使GDL成為萬能工具:在社交媒體、藥物發(fā)現(xiàn)、芯片植入、預測、生物信息學等方面都顯示出了很大的前景。
本文將流行的圖神經(jīng)網(wǎng)絡及其數(shù)學細微差別的進行詳細的梳理和解釋,圖深度學習背后的思想是學習具有節(jié)點和邊的圖的結構和空間特征,這些節(jié)點和邊表示實體及其交互。
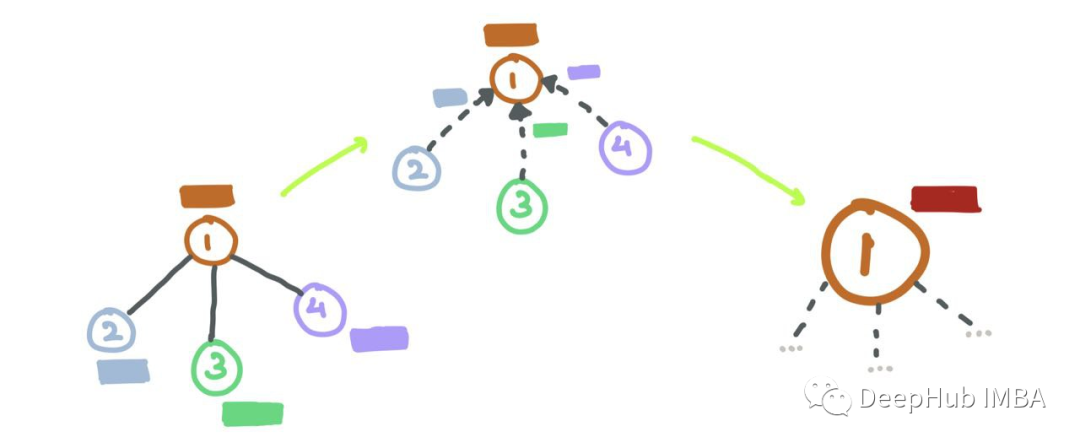
圖
在我們進入圖神經(jīng)網(wǎng)絡之前,讓我們先來探索一下計算機科學中的圖是什么。
圖G(V,E)是包含一組頂點(節(jié)點)i∈v和一組連接頂點i和j的邊eij∈E的數(shù)據(jù)結構,如果連接兩個節(jié)點i和j,則eij=1,否則eij=0。可以將連接信息存儲在鄰接矩陣A中:

我假設本文中的圖是無加權的(沒有邊權值或距離)和無向的(節(jié)點之間沒有方向關聯(lián)),并且假設這些圖是同質(zhì)的(單一類型的節(jié)點和邊;相反的是“異質(zhì)”)。
圖與常規(guī)數(shù)據(jù)的不同之處在于,它們具有神經(jīng)網(wǎng)絡必須尊重的結構;不利用它就太浪費了。下面的圖是一個社交媒體圖的例子,節(jié)點是用戶,邊是他們的互動(比如關注/點贊/轉(zhuǎn)發(fā))。

對于圖像來說,圖像本身就是一個圖!這是一種叫做“網(wǎng)格圖”的特殊變體,其中對于所有內(nèi)部節(jié)點和角節(jié)點,來自節(jié)點的外向邊的數(shù)量是恒定的。在圖像網(wǎng)格圖中存在一些一致的結構,允許對其執(zhí)行簡單的類似卷積的操作。
圖像可以被認為是一種特殊的圖,其中每個像素都是一個節(jié)點,并通過虛線與周圍的其他像素連接。當然,以這種方式查看圖像是不切實際的,因為這意味著需要一個非常大的圖。例如,32×32×3的一個簡單的CIFAR-10圖像會有3072個節(jié)點和1984條邊。對于224×224×3的較大ImageNet圖像,這些數(shù)字會更大。
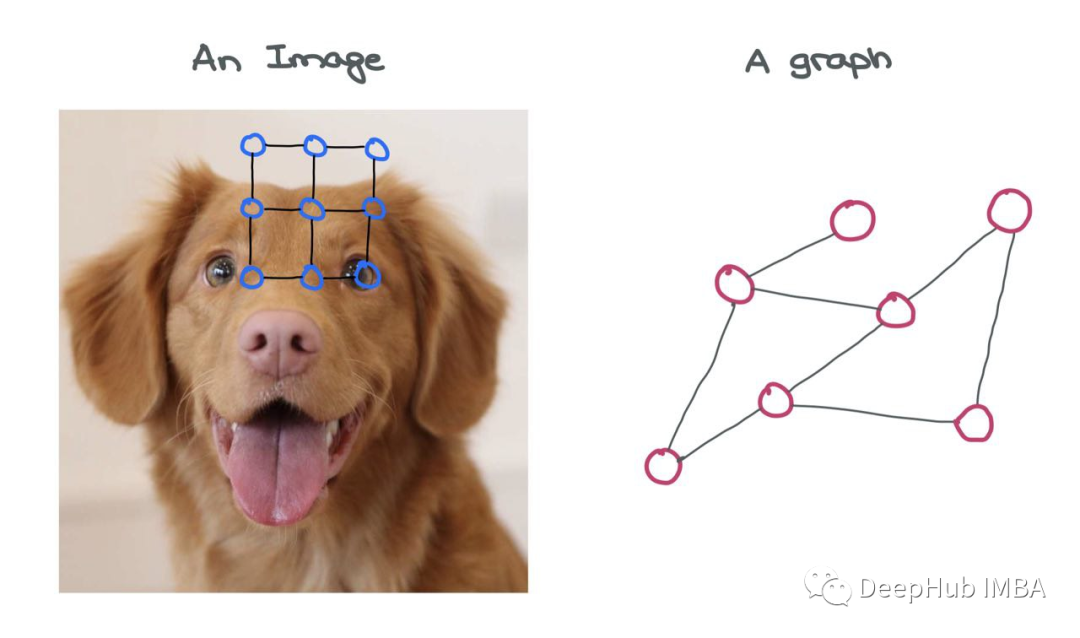
與圖片相比,圖的不同的節(jié)點與其他節(jié)點的連接數(shù)量不同,并且沒有固定的結構,但是就是這種結構為圖增加了價值。
圖神經(jīng)網(wǎng)絡
單個圖神經(jīng)網(wǎng)絡(GNN)層有一堆步驟,在圖中的每個節(jié)點上會執(zhí)行:
- 消息傳遞
- 聚合
- 更新
這些組成了對圖形進行學習的構建塊,GDL的創(chuàng)新都是在這3個步驟的進行的改變。
節(jié)點
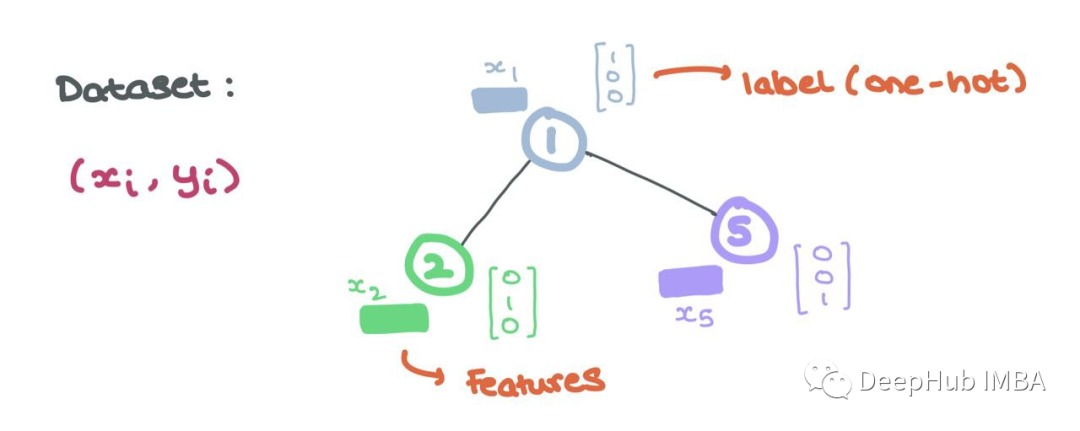
節(jié)點表示一個實體或?qū)ο螅缬脩艋蛟印R虼斯?jié)點具有所表示實體的一系列屬性。這些節(jié)點屬性形成了節(jié)點的特征(即“節(jié)點特征”或“節(jié)點嵌入”)。
通常,這些特征可以用Rd中的向量表示. 這個向量要么是潛維嵌入,要么是以每個條目都是實體的不同屬性的方式構造的。
例如,在社交媒體圖中,用戶節(jié)點具有可以用數(shù)字表示的年齡、性別、政治傾向、關系狀態(tài)等屬性。在分子圖中,原子節(jié)點可能具有化學性質(zhì),如對水的親和力、力、能量等,也可以用數(shù)字表示。
這些節(jié)點特征是GNN的輸入,每個節(jié)點i具有關聯(lián)的節(jié)點特征xi∈Rd和標簽yi(可以是連續(xù)的,也可以是離散的,就像單獨編碼一樣)。
邊
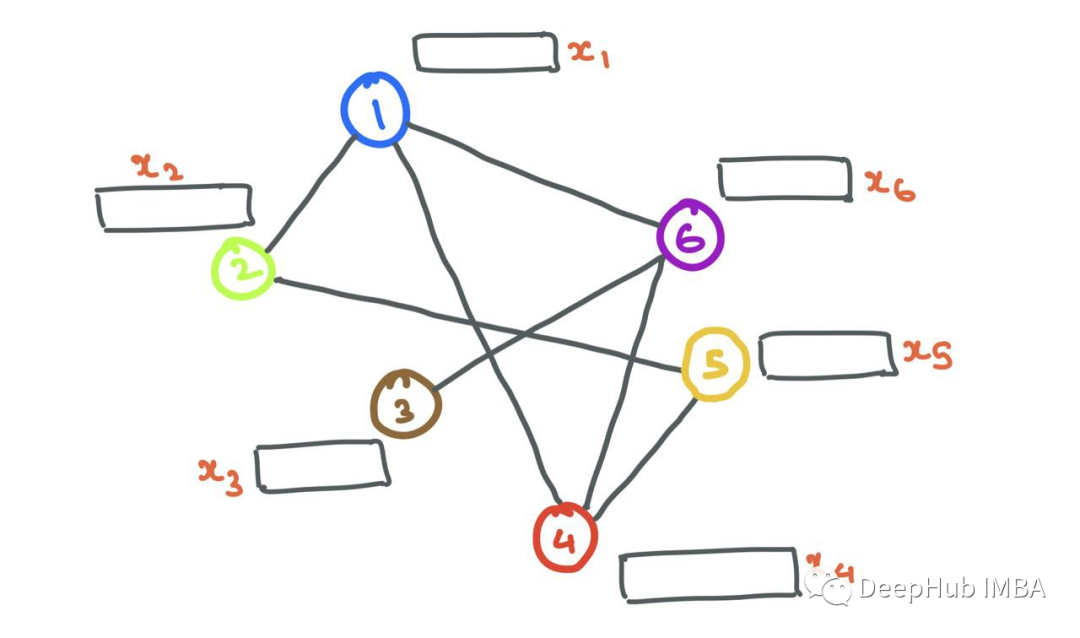
邊也可以有特征aij∈Rd '例如,在邊緣有意義的情況下(如原子之間的化學鍵)。我們可以把下面的分子想象成一個圖,其中原子是節(jié)點,鍵是邊。雖然原子節(jié)點本身有各自的特征向量,但邊可以有不同的邊特征,編碼不同類型的鍵(單鍵、雙鍵、三鍵)。不過為了簡單起見,在本文中我將省略邊的特性。

現(xiàn)在我們知道了如何在圖中表示節(jié)點和邊,讓我們從一個具有一堆節(jié)點(具有節(jié)點特征)和邊的簡單圖開始。
消息傳遞
gnn以其學習結構信息的能力而聞名。通常,具有相似特征或?qū)傩缘墓?jié)點相互連接(比如在社交媒體中)。GNN利用學習特定節(jié)點如何以及為什么相互連接,GNN會查看節(jié)點的鄰域。
鄰居Ni,節(jié)點I的集合定義為通過邊與I相連的節(jié)點j的集合。形式為Ni={j: eij∈E}。
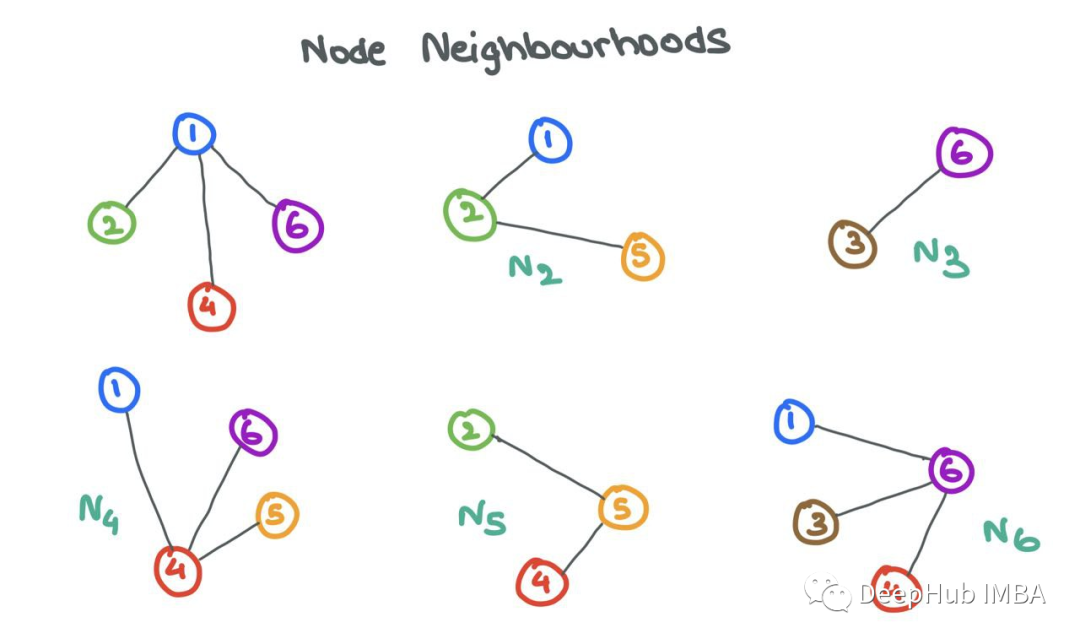
一個人被他所處的圈子所影響。類似地GNN可以通過查看其鄰居Ni中的節(jié)點i來了解很多關于節(jié)點i的信息。為了在源節(jié)點i和它的鄰居節(jié)點j之間實現(xiàn)這種信息共享,gnn進行消息傳遞。
對于GNN層,消息傳遞被定義為獲取鄰居的節(jié)點特征,轉(zhuǎn)換它們并將它們“傳遞”給源節(jié)點的過程。對于圖中的所有節(jié)點,并行地重復這個過程。這樣,在這一步結束時,所有的鄰域都將被檢查。
讓我們放大節(jié)點6并檢查鄰域N6={1,3,4}。我們?nèi)∶總€節(jié)點特征x1、x3和x4,用函數(shù)F對它們進行變換,函數(shù)F可以是一個簡單的神經(jīng)網(wǎng)絡(MLP或RNN),也可以是仿射變換F(xj)=Wj?xj+b。簡單地說,“消息”是來自源節(jié)點的轉(zhuǎn)換后的節(jié)點特征。

F 可以是簡單的仿射變換或神經(jīng)網(wǎng)絡。現(xiàn)在我們設F(xj)=Wj?xj為了方便計算 ? 表示簡單的矩陣乘法。
聚合
現(xiàn)在我們有了轉(zhuǎn)換后的消息{F(x1),F(xiàn)(x3),F(xiàn)(x4)}傳遞給節(jié)點6,下面就必須以某種方式聚合(“組合”)它們。有很多方法可以將它們結合起來。常用的聚合函數(shù)包括:

假設我們使用函數(shù)G來聚合鄰居的消息(使用sum、mean、max或min)。最終聚合的消息可以表示為:
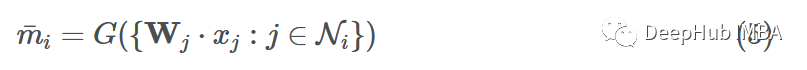
更新
使用這些聚合消息,GNN層就要更新源節(jié)點i的特性。在這個更新步驟的最后,節(jié)點不僅應該知道自己,還應該知道它的鄰居。這是通過獲取節(jié)點i的特征向量并將其與聚合的消息相結合來操作的,一個簡單的加法或連接操作就可以解決這個問題。
使用加法

其中σ是一個激活函數(shù)(ReLU, ELU, Tanh), H是一個簡單的神經(jīng)網(wǎng)絡(MLP)或仿射變換,K是另一個MLP,將加法的向量投影到另一個維度。
使用連接:
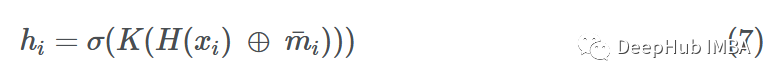
為了進一步抽象這個更新步驟,我們可以將K看作某個投影函數(shù),它將消息和源節(jié)點嵌入一起轉(zhuǎn)換:

初始節(jié)點特征稱為xi,在經(jīng)過第一GNN層后,我們將節(jié)點特征變?yōu)閔i。假設我們有更多的GNN層,我們可以用hli表示節(jié)點特征,其中l(wèi)是當前GNN層索引。同樣,顯然h0i=xi(即GNN的輸入)。
-
芯片
+關注
關注
456文章
51019瀏覽量
425416 -
神經(jīng)網(wǎng)絡
+關注
關注
42文章
4776瀏覽量
100952 -
數(shù)學
+關注
關注
0文章
99瀏覽量
19265
發(fā)布評論請先 登錄
相關推薦
matlab 神經(jīng)網(wǎng)絡 數(shù)學建模數(shù)值分析
matlab 中亮劍數(shù)學 全面掌握控制 神經(jīng)網(wǎng)絡就在腳下
關于開關磁阻電機的matlab BP神經(jīng)網(wǎng)絡數(shù)學建模方面的資料
【PYNQ-Z2試用體驗】神經(jīng)網(wǎng)絡基礎知識
如何構建神經(jīng)網(wǎng)絡?
卷積神經(jīng)網(wǎng)絡的數(shù)學原理介紹
深入卷積神經(jīng)網(wǎng)絡背后的數(shù)學原理
深度:了解訓練神經(jīng)網(wǎng)絡時所用到的數(shù)學過程
圖解:卷積神經(jīng)網(wǎng)絡數(shù)學原理解析
詳解圖神經(jīng)網(wǎng)絡的數(shù)學原理2
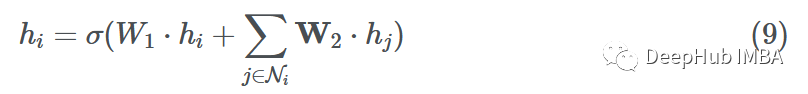
詳解圖神經(jīng)網(wǎng)絡的數(shù)學原理3
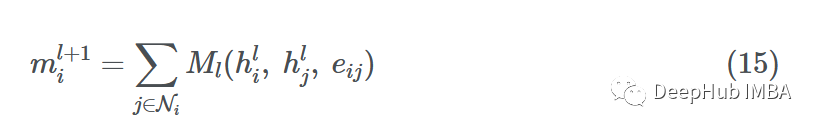




 詳解圖神經(jīng)網(wǎng)絡的數(shù)學原理1
詳解圖神經(jīng)網(wǎng)絡的數(shù)學原理1










評論