特定消諧技術是通過計算PWM波的開關時刻,消除特定的低階諧波。 其基本理論是恰當地控制逆變器脈寬調制電壓的波形,通過脈寬平均法把逆變器輸出的方波電壓轉換成等效的正弦波,以消除某些特定的諧波。 本文對特定諧波消除方法的基本原理進行介紹。
01SHEPWM的基本原理
以單相 SHEPWM 輸出的雙極性電壓波形為例, 對逆變器輸出電壓波形進行傅里葉分析。 三相 SHEPWM 輸出波形中的 B 相和 C 相波形,只需將單相波形移相 120°和 240°即可得到。 逆變器雙極性輸出電壓波形如圖 1所示。
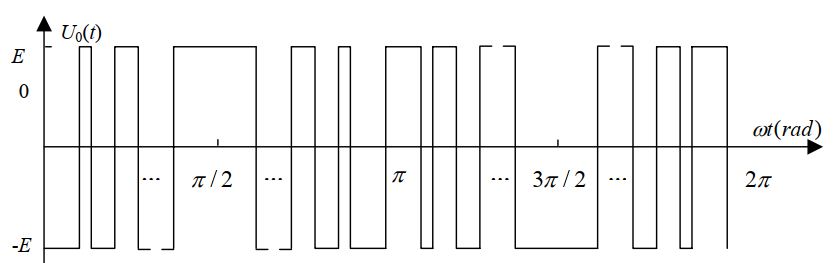
圖 1 雙極性 SHEPWM 輸出電壓波形
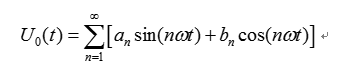
其中:
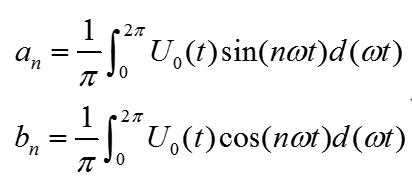
由于圖 1中輸出電壓波形 U(t)為奇函數,又是奇諧函數,即 U0(t)在[0, π]區間以 π/2 為軸對稱,在[0, 2π]區間以 π 點對點對稱,因此有:
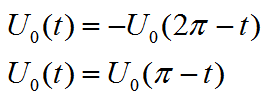
因此傅利葉分解式中的直流分量、余弦分量和偶次正弦分量系數為零,其傅里葉分解系數可簡化為:
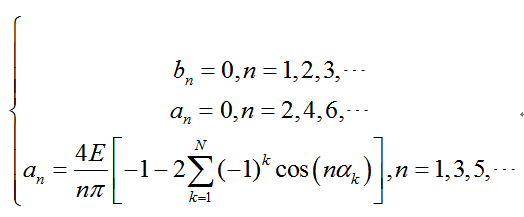
如果令 q( q=a1/vdc,量綱一)為選定的基波幅值,令其他 N -1 個低階的高次諧波的幅值為零,則有:
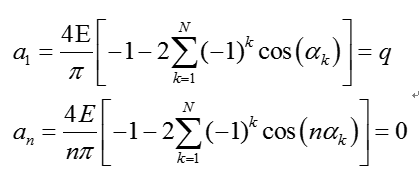
上方程組即為逆變器雙極性輸出單相特定消諧數學模型,N 表示在[0,π/2]區間內開關角的數量, αk 為區間內 N 個開關角中的第 k 個開關角, n為基波和各次諧波的次數。 求解方程組可得到一組在[0,π/2]區間內的脈沖波開關角,再由輸出波形的奇諧對稱性,可以求得整個周期內的開關角位置。 采用這組開關角控制逆變器,其輸出PWM 波形保證了基波幅值為規定的數值,同時也使N-1個指定階次的諧波幅值為零(N個開關角解N個方程,可以決定一個基波幅值以及N-1個指定階次的諧波幅值)。 式中開關角應滿足:
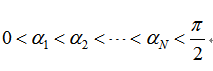
對于三相對稱系統,三的整數倍次諧波因同相而被自動消除,故上中的 n 只對非三的整數倍的奇數才有意義,所以有:
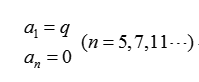
上公式雙極性輸出三相特定消諧數學模型。 式中共有 N 個獨立變量a1,a2,…,aN,最多可消除 N-1個非三的倍數次的低次諧波。
綜上可知,特定諧波消除技術的數學模型是一組非線性方程組,具有如下特點:
1. 方程組非線性,自變量以三角函數形式存在;
2. 求解只能采用數值方法求解,且求解過程較復雜;
3. 傳統的牛頓迭代法由于其局部收斂性使求解對初值要求嚴格,且求解速度慢,收斂性差。
基于以上因素的影響,使在線求解開關角受到限制,限制了該技術的實時應用。
通過以上建模分析可知,特定消諧 PWM 的核心是非線性方程組的求解,只能通過數值方法迭代求解,通常對迭代序列有三個要求:
1. 迭代序列的適定性。 即要求迭代程序得到的解要滿足定義域的要求。
2. 迭代序列的收斂性。 即要求迭代序列隨迭代次數的增加收斂于方程的精確解。
3. 迭代序列的收斂速度與效率。 迭代序列收斂的快慢及計算時間的長短是衡量迭代法優劣的主要指標。
目前,牛頓迭代法是常用的特定消諧方程求解方法。 作者建立了SHEPWM的simulink仿真模型,將牛頓迭代求解開關角的方法寫成函數形式,在選取四分之一周期的開關角N之后,通過該函數離線計算各調制度下的開關角曲線,形成lookup
table。 在三相兩電平逆變器上驗證該SHEPWM調制算法。
Simulink仿真模型文件:

該Simulink模型主要包含一下內容:
a.編寫了牛頓同倫子函數SHEPWM_Angle_Cal_TongLun.m
函數輸入(N,m)分別為四分之一開關角個數,調制度數組。
b. 編寫了牛頓迭代子函數SHEPWM_Angle_Cal_Newton.m
函數輸入(N,m,Angle_init)分別為四分之一開關角個數,調制度數組,各個調制度對應的開關角初值Angle_init為(Nlength(m))維數組,輸出值為Nlength(m)維數組,對應調制度m取值不同時的N個開關角度。
c.編寫主函數SHEPWM_Modulation.m,該函數被仿真模型TwoLevelInverter_SHEPWM.slx自動調用,根據對開關角個數的取值N,
計算不同調制度對應的開關角矩陣。
d.搭建仿真模型TwoLevelInverter_SHEPWM.slx,該仿真模型自動調用主函數SHEPWM_Modulation.m,根據對開關角個數取值N,
計算不同調制度對應的開關角矩陣。 界面如下:
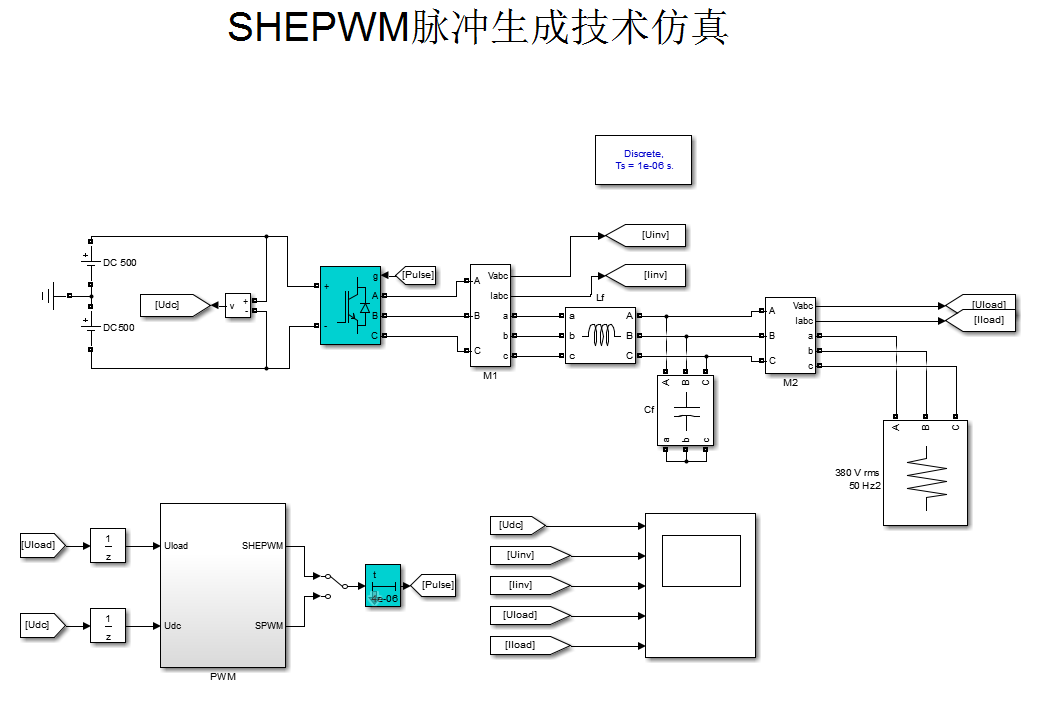
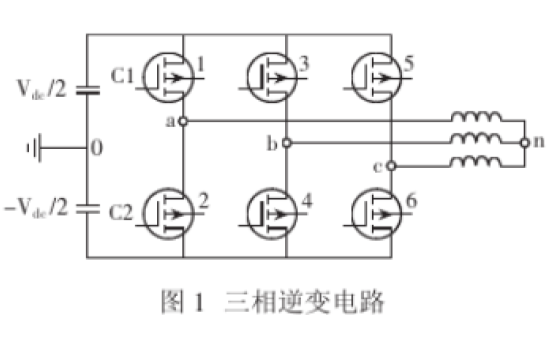
主要分為三相兩電平逆變電路及其負載,示波器部分,和調制部分。 其中包含SHEPWM調制以及SPWM調制,通過手控開關切換。 SHEPWM調制部分如下:
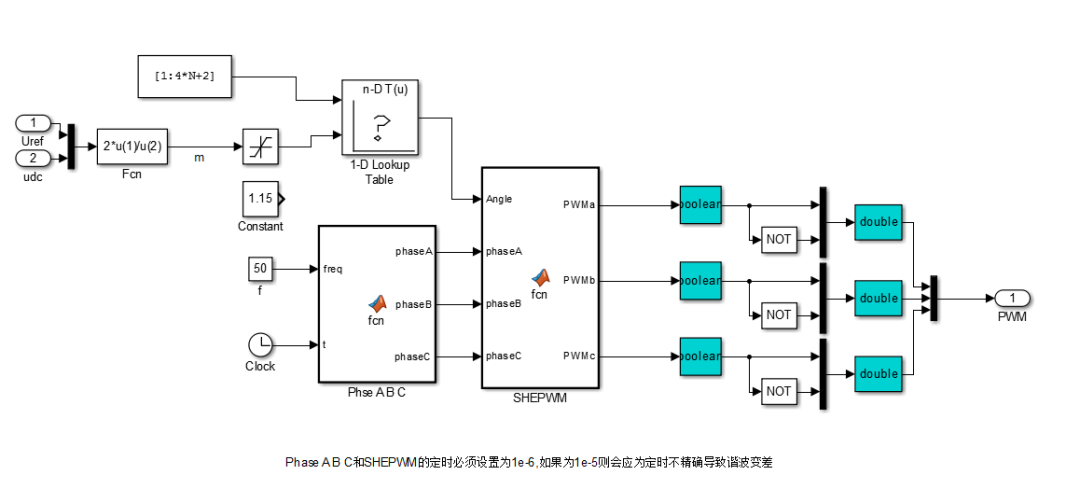
通過主函數SHEPWM_Modulation.m得到不同調制度對應的開關角矩陣。 插入上圖的查表模塊中,根據不同的調制度輸入,得到SHEPWM脈沖。 波形如下。
a.N取值33時,運行仿真模型,模型調用SHEPWM_Modulation.m后會計算SHEPWM開關角的同時,會輸出如下同倫迭代算法所求開關角軌跡圖和牛頓迭代算法所求開關角軌跡圖。
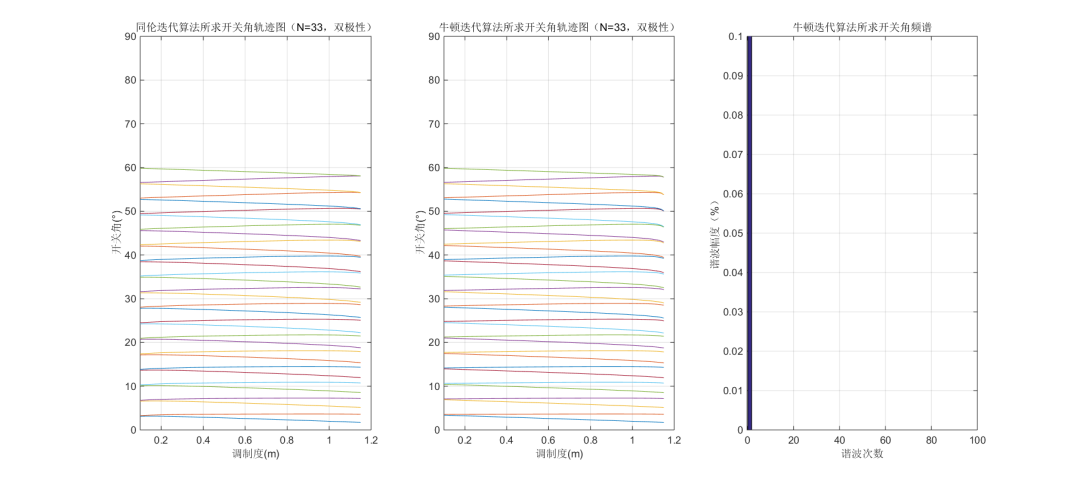
b. 直流側電壓,LC濾波器前輸出電壓,LC濾波器前輸出電流,LC濾波器后輸出電壓,LC濾波器后輸出電流波形如下:
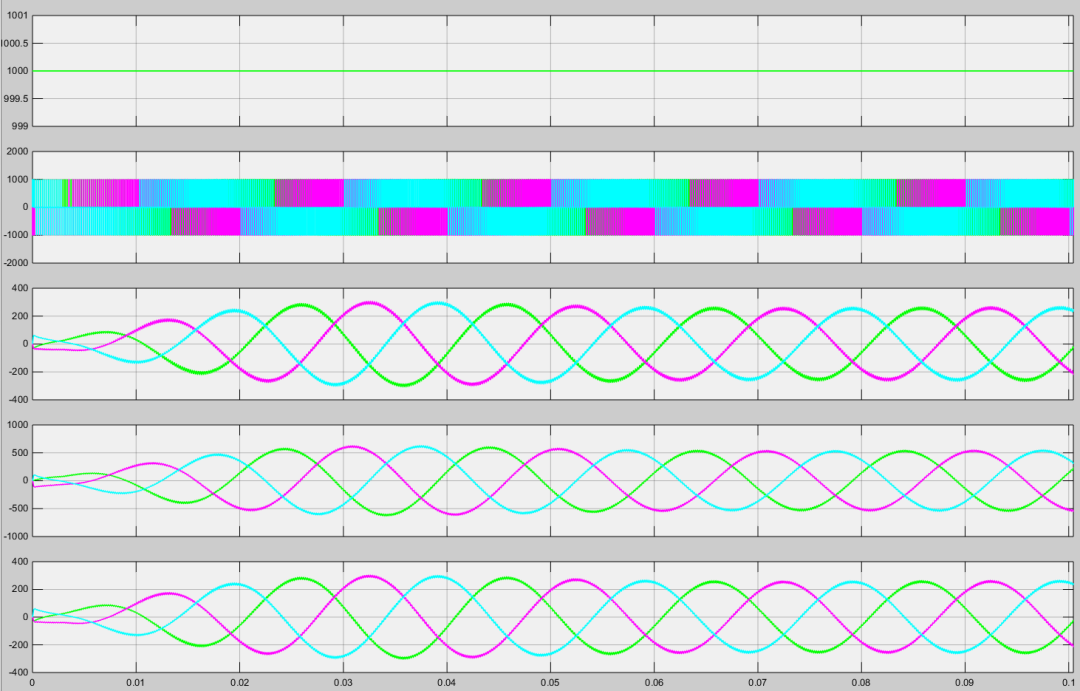
c. 濾波前輸出電壓諧波如下:
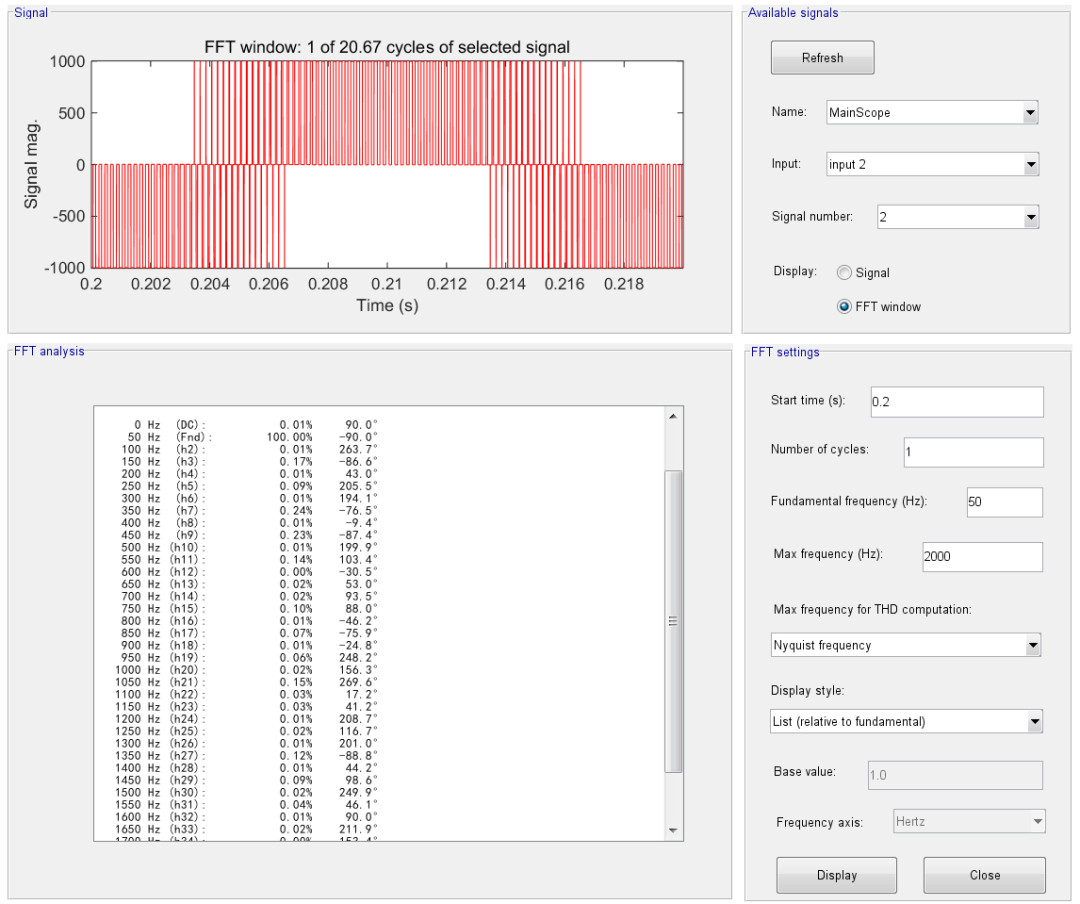
d. 濾波后輸出電壓諧波如下:
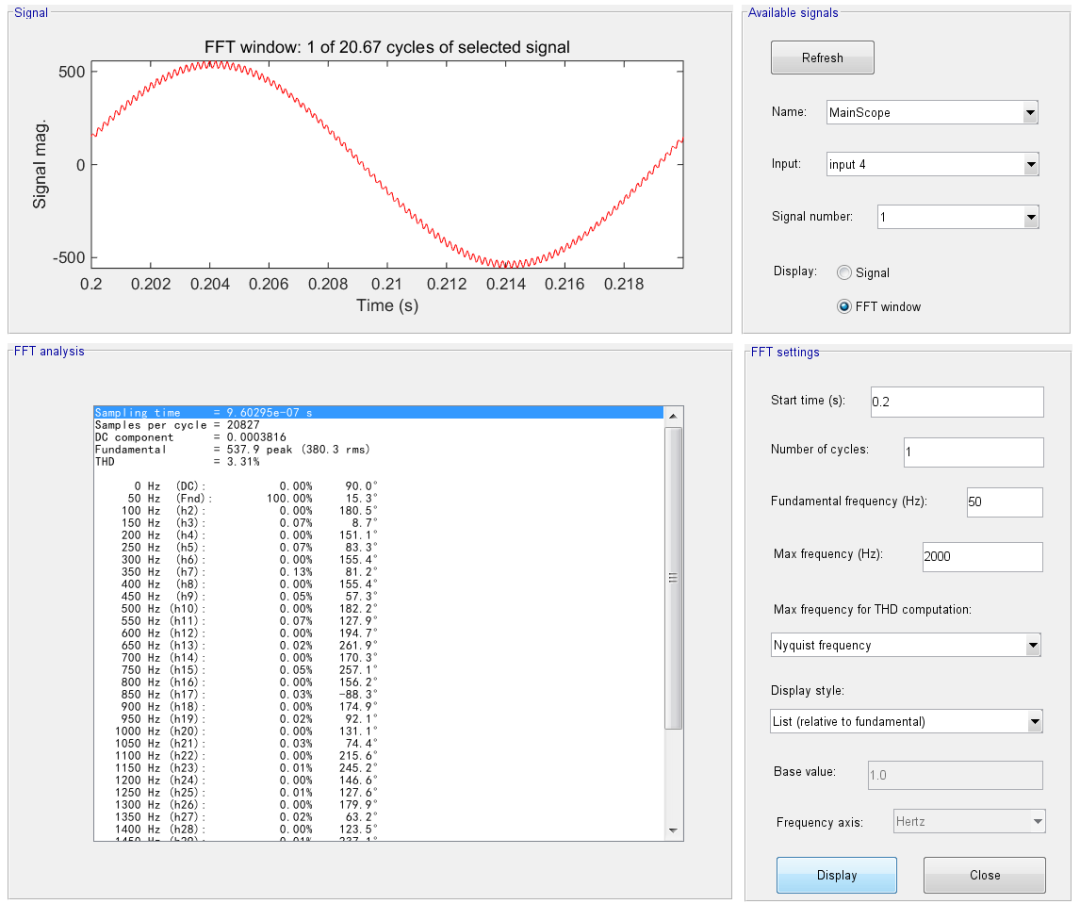
該模型使用十分方便,對四分之一周期取不同開關角時,只需要修改主函數m文件中N的定義即可求解,另外m文件中包含了豐富的注釋,便于理解算法。
-
PWM
+關注
關注
114文章
5186瀏覽量
213957 -
逆變器
+關注
關注
283文章
4722瀏覽量
206832 -
仿真
+關注
關注
50文章
4082瀏覽量
133613 -
Simulink
+關注
關注
22文章
535瀏覽量
62402 -
SHEPWM
+關注
關注
0文章
8瀏覽量
8075
發布評論請先 登錄
相關推薦
SPWM的基本原理是什么?
線性電源的基本原理是什么
無線充電的基本原理是什么
磁懸浮列車牽引控制的Simulink仿真
SIMULINK仿真
如何使用SIMULINK對SVPWM算法進行仿真
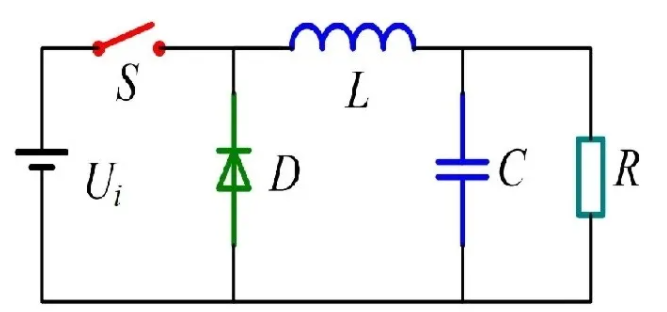
Buck電路的基本原理,Simulink模型的獲取方式
永磁同步電機FOC控制的基本原理及Matlab/Simulink仿真分析
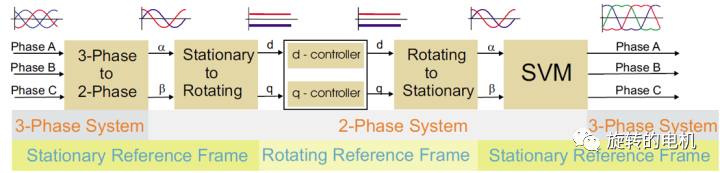
SVPWM控制技術的基本原理及Matlab/Simulink仿真分析





 SHEPWM的基本原理和Simulink仿真
SHEPWM的基本原理和Simulink仿真











評論