幾個網紅問題
之前的文章介紹了Buck在模擬控制中,常見的PWM調制與對應的控制方式:
談及控制必有環路,而提到環路則會條件反射想到小信號建模。 《模擬電子技術》就曾詳細介紹三極管/ MOSFET組成的放大電路其大小信號分析,對以Buck為代表的開關電源來說同理,有小信號模型也必然有大信號模型,那么:
| 問題1 | 大小信號模型各自代表了什么含義,能解決何種問題? |
|---|---|
| 問題2 | 為何一談到環路,大家就默認使用小信號模型,而不顧物理意義涵蓋更廣的大信號模型? |
| 問題3 | 教科書上傳統的“平均模型”存在哪些懸而未決的問題? 為何說小信號環路的“穿越頻率/截止頻率”要設計在開關頻率的1/10-1/5范圍內? |
| 問題4 | 教科書外其他建模的手段都有哪些,如何分類及和“平均模型”的相互聯系? |
| 問題5 | 大信號穩定性和小信號穩定性的關系? 如何看待低頻極限環振蕩和次諧波振蕩? |
筆者曾在大四研一入門建模的階段被這些問題困擾,本文想繼續圍繞模擬控制的Buck電路,不引入任何公式,以綜述性質討論它們的答案。
大信號與小信號的關系
觀察一條曲線函數f(x),位于該曲線上有一點(X0,Y0),可在該點求取微分作切線,從而實現局部的線性化,得到一條在X0處附近,小擾動范圍內和原先曲線等效的直線。
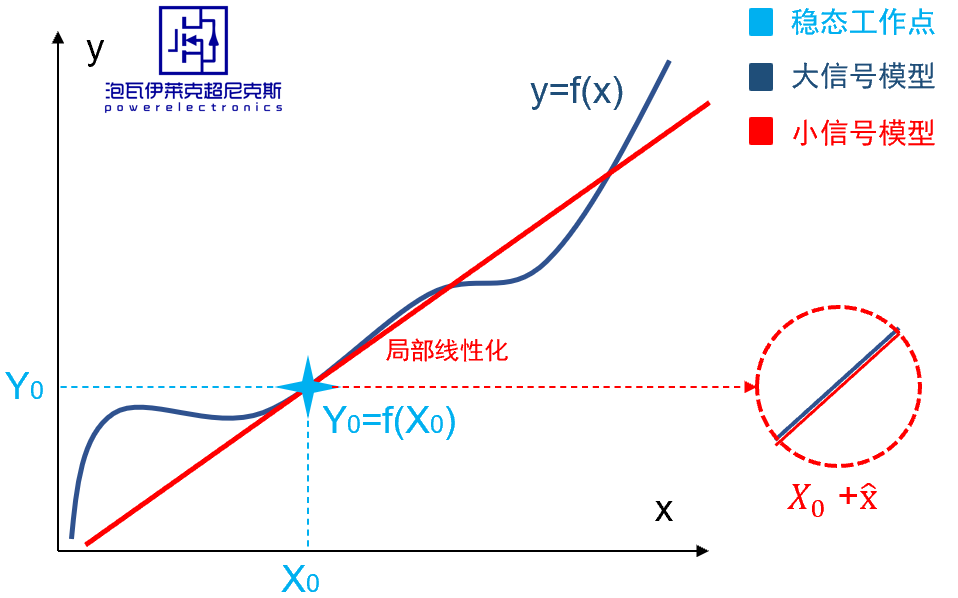
實際的開關變換器系統,包含多個狀態變量和輸入輸出,遠比一元函數復雜,但穩態工作點和大小信號的內涵是類似的。 一元函數曲線上每個點相當于每個穩態工作點,x在曲線上大幅移動相當于跨越多個穩態工作點的變工作點過程,而x停在X0處附近作小信號擾動,從而局部線性化,恰相當于在某個穩態工作點附近注入小信號擾動的輸入,從而求取對應輸出的,線性化的小信號模型。
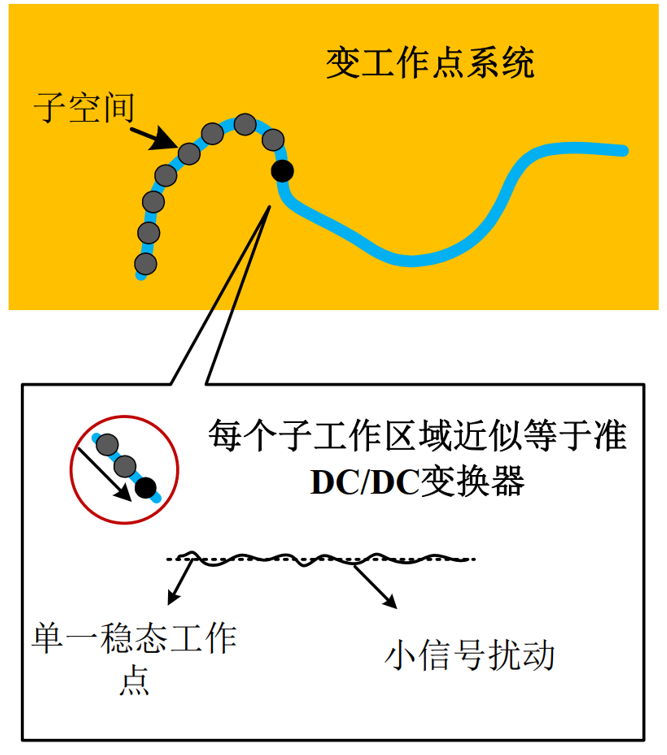
| 穩態模型 | 穩態分析(DC分析) | 描述開關電源穩定運行狀態用作穩態分析 |
|---|---|---|
| 功率開關器件、儲能元件及變壓器等設計的基礎 | ||
| 大信號模型 | 大信號分析 | 可描述大信號擾動下,開關電源變工作點(跨越多個穩態工作點)性能的非線性模型 |
| 是無數個穩態工作點的組合,在整個信號范圍內均有效,能夠描述全局的動力學行為和變化規律 | ||
| 小信號模型 | 小信號分析(AC分析) | 在某個穩態工作點附近注入小擾動信號,進行擾動分離和線性化處理后,得到的頻率響應模型 |
由此回答 問題1和2 ,按某穩態工作點局部線性化得到的小信號模型設計的環路,嚴格來說只能適用于該穩態工作點附近的穩定性與動態分析,并不能用于電路有大幅波動,使得工作點偏離從而連續跨越多個穩態工作點的情況 ,如大擺幅動態,零狀態啟機等工況,主要原因在于不同工作點的小信號模型可能完全不同,使用同一套控制環路參數,可能導致部分工作點附近的動態表現遠不及預期,甚至不穩定而發散。 這些情況應當使用大信號模型處理。
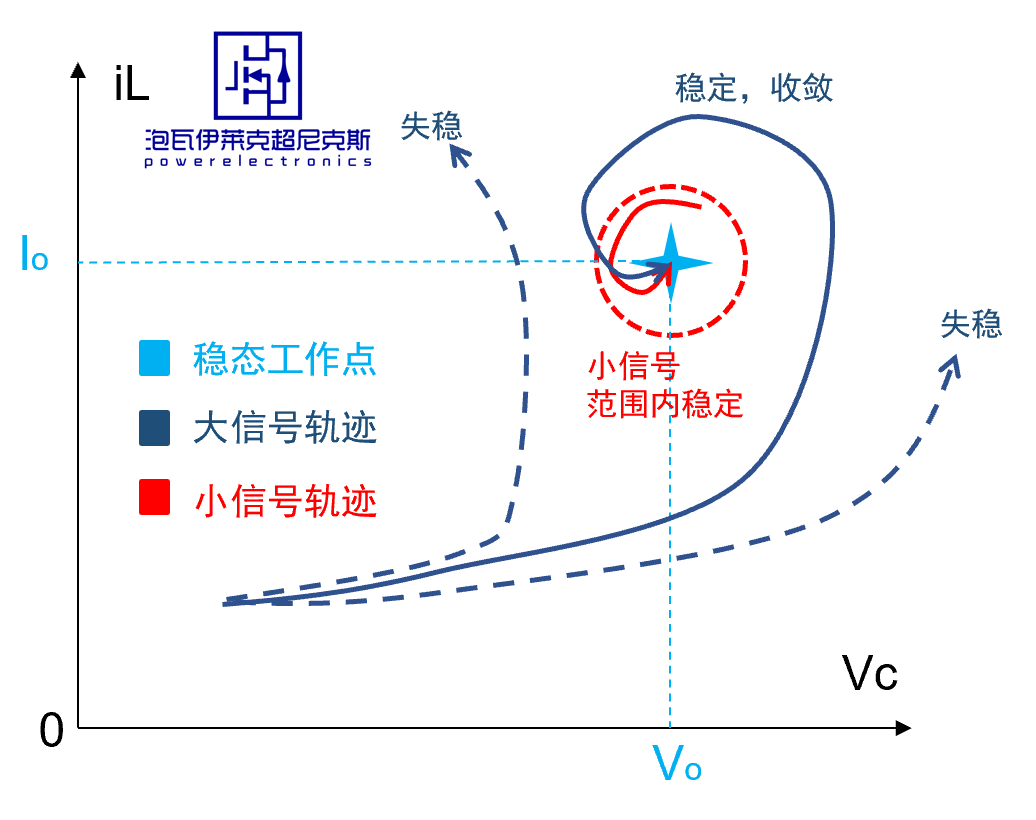
然而,為了避免處理大信號這樣的非線性系統, 實際工程中只要參數設計得合理,負反饋控制系統本身就有一定的“魯棒性”,且功率主電路的非線性并不十分強烈,使用同一套環路參數穿越多個工作點往往也是可行的,雖然一定不是最優的。
開關變換器的模型特點
針對我們最熟悉的線性時不變(LTI)系統,經典控制理論基于拉氏變換和頻率特性傳遞函數的形式,提供了大量的分析工具,如波特圖和穩定裕量判據等。 開關變換器是非線性,時變,高階,離散,病態的系統,尤其非線性和時變這兩大特點,阻礙了經典控制理論模型的建立和使用,必須找到辦法逐一解決。
| 非線性 |
|---|
| 執行機構如PWM調制器,存在上下限幅行為,在大幅波動情況下特性發生改變* 每個周期中,開關管會在電阻區和截止區之間切換,需要分段解析* 元器件本身的非線性 |
| 時變 |
| PWM調制器在高頻調制下,會引起時變效應 |
| 高階 |
| 考慮雜散參數或使用含多個LC的復雜拓撲,獨立儲能元件個數多,存在多狀態量回路 |
| 離散 |
| 開關管開和關期間,電路拓撲結構不同* PWM調制器有采樣保持器特性 |
| 病態 |
| 功率主電路的“時間常數”遠大于控制環路的“時間常數”,且整個系統中存在PWM控制脈沖的邊沿/周期,驅動和開關脈沖的邊沿/周期,電磁能量脈沖的邊沿/周期,傳感器采樣周期,快速或慢速負載變化的邊沿/周期等不同時間計量單位,是多時間尺度系統 |
傳統平均模型及其缺陷
如下展示了傳統的開關平均模型求取大信號模型和小信號模型手法及對應關系。
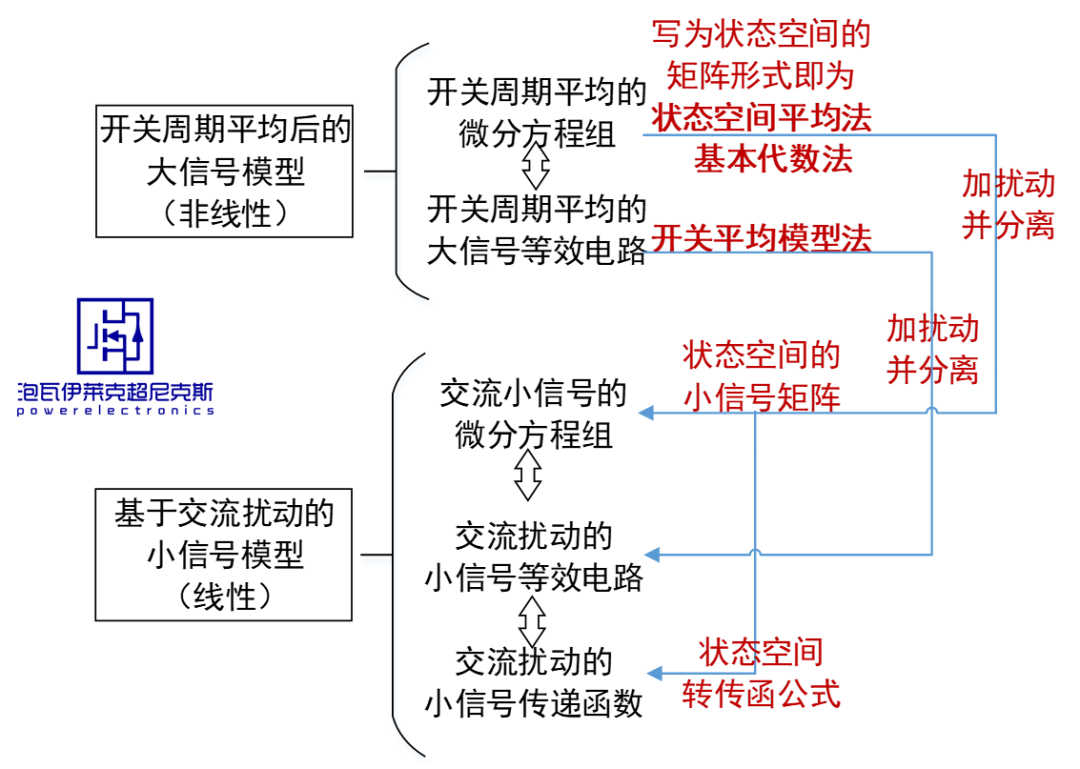
以Buck為例,為了把主電路中非線性的開關網絡直接平均化,會要求滿足“低頻”假設和“小紋波”假設。 電路中看不到開關頻率及諧波及其邊頻帶的任何信息,從而移除開關動作造成的非線性影響。
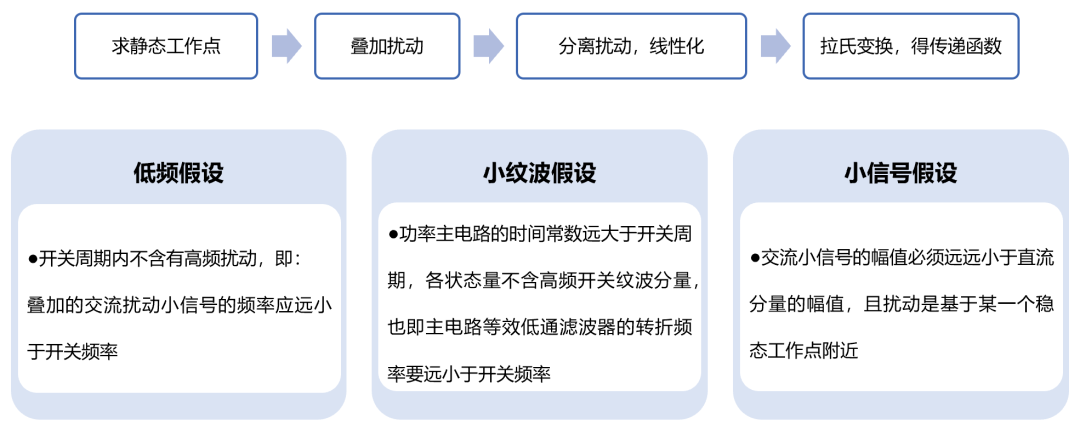
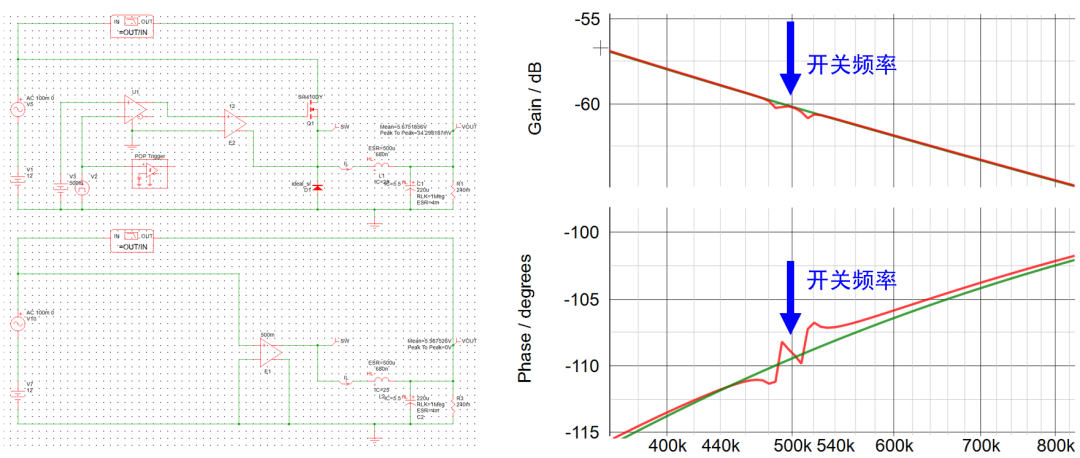
這種平均思想的代價也是顯而易見的:線性化后的頻率特性無法反應高頻(開關頻率附近)的特征。 由于環路的帶寬遠離開關頻率,設計者對高頻特性并不關心,這種假設是完全可以接受的。
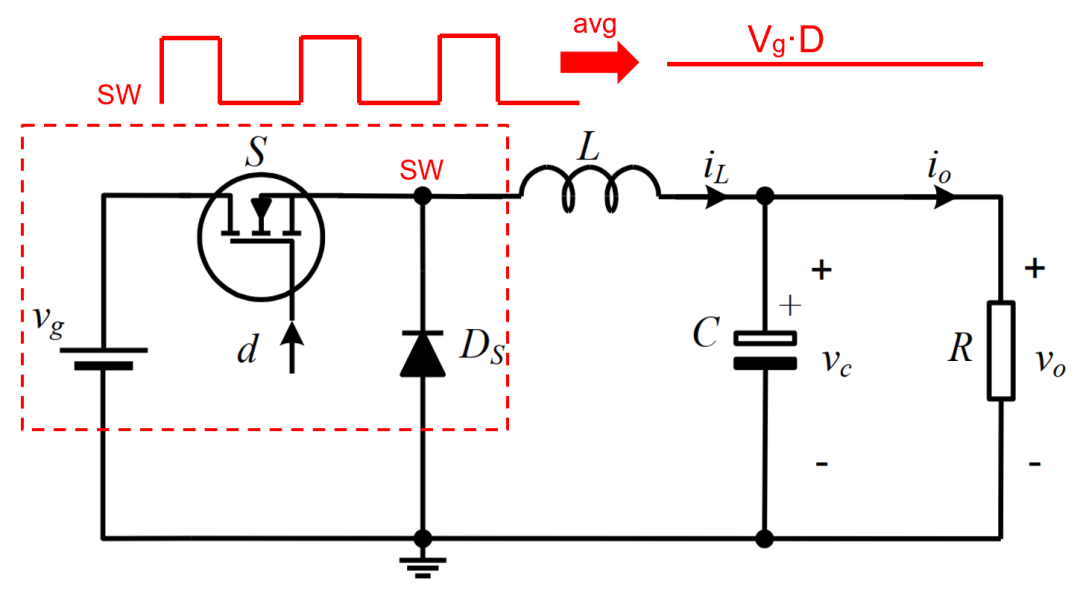
需要注意,Buck類型的變換器,包含的非線性開關網絡是最容易平均簡化為線性模型的,也導致了Buck類平均模型導出的小信號模型與穩態工作點無關,其他拓撲勢必會更加復雜。
上述均是針對功率主電路中的非線性開關網絡的,并未包含PWM調制器的處理。 除非是一個完全由方波發生器產生PWM而開環運行,一個閉環控制的環路必包含PWM調制器的模型。
下圖描述了“基于平均值的比較行為”的PWM調制器,這種最基本的調制方式可直接對應到單電壓環模式/平均電流模式。 圖中紅色信號verr為補償器的輸出作為調制波,藍色信號為開關頻率的載波vsaw。
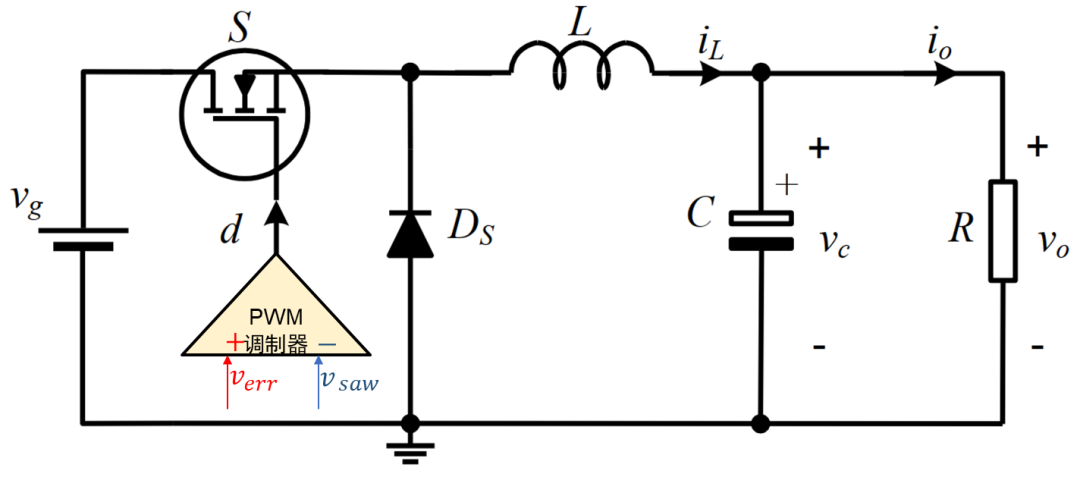
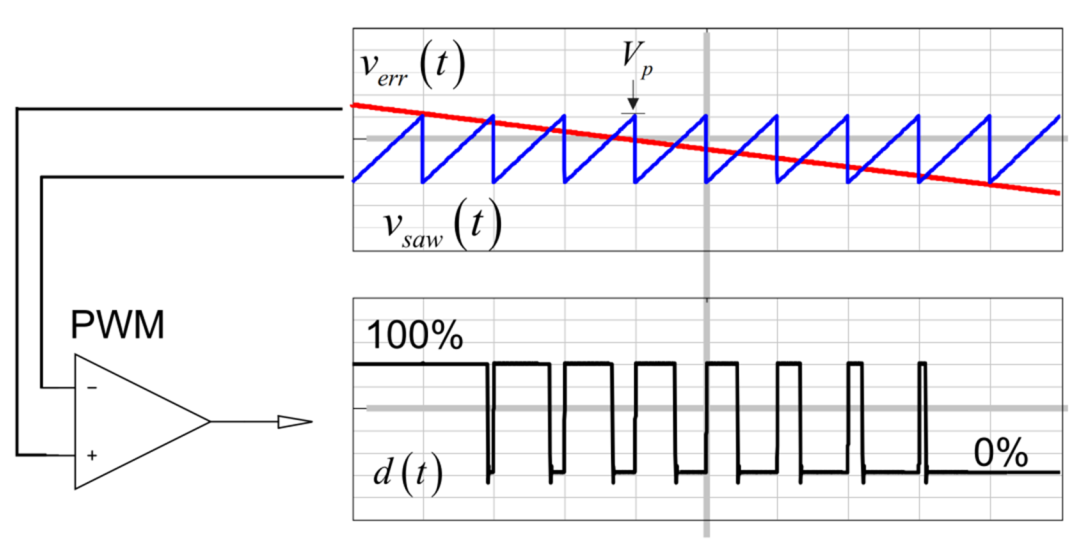
當調制波verr緩慢變化(頻率較低)時,PWM調制器被建模為一個純比例環節是完全合理的。 該環節配合主電路的平均模型,結合補償器,一起組成了傳統平均法完整的閉環環路。
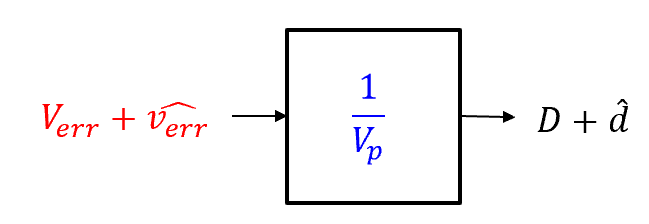
然而,當調制波verr快速變化(頻率較高)時,PWM調制器的輸出與調制波輸入的時刻相關,系統是時變系統,難以用傳遞函數描述。
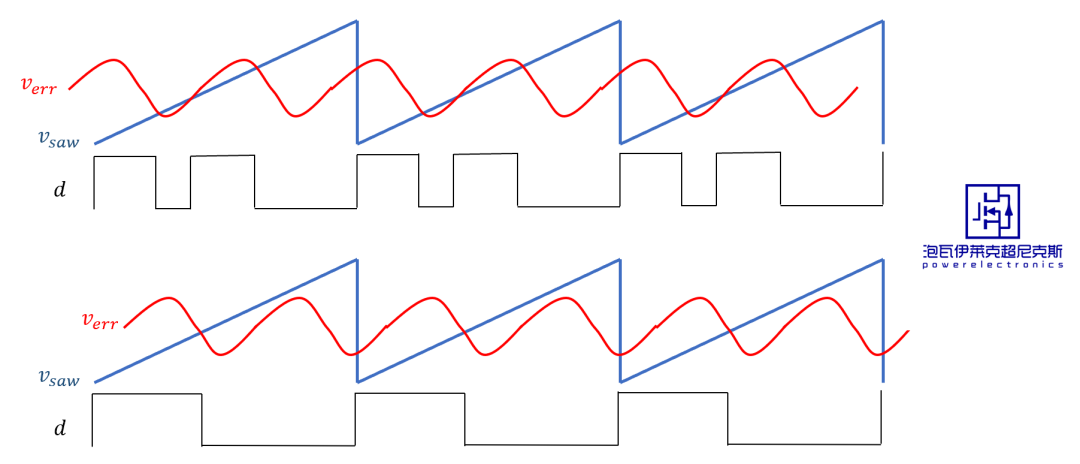
為了方便推導小信號模型,假設調制波verr近似為低頻信號,故而PWM調制器和整個系統可當作時不變系統處理,這便是平均模型成立的 “時不變”假設 。
需要注意, “時不變”假設是閉環環路進一步限制傳統平均模型的有效頻率范圍的核心因素 ,相比非線性的開關網絡,它會在更低的頻率處體現出平均模型的失準。
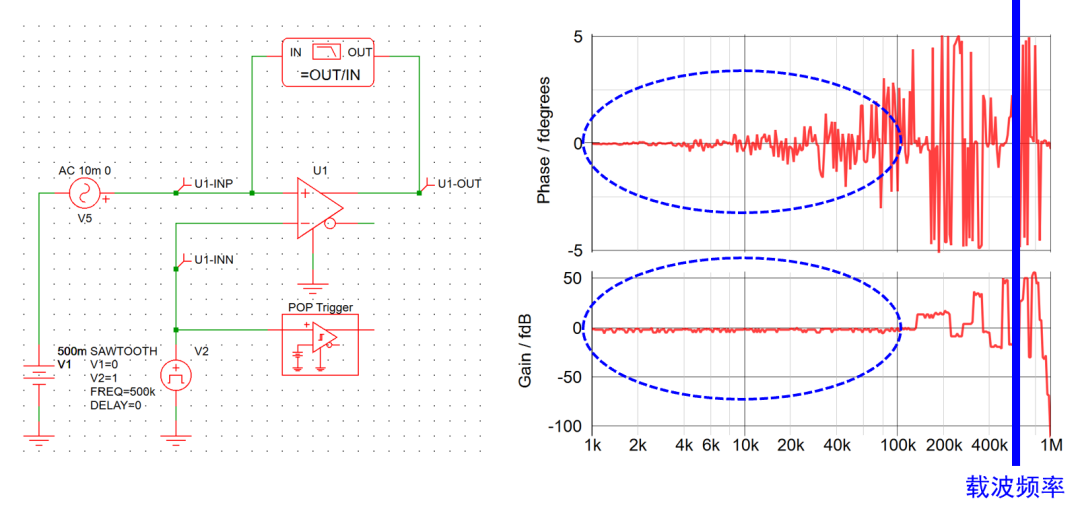
由此回答 問題3 ,當實測頻率特性時,注入的擾動輸入頻率較高時,PWM調制器的時變特性會導致依據傳統平均模型求得的小信號模型,在fsw以內并不高的頻率處開始,Phase曲線和實際相比已經失準,導致環路的設計只能被限制在相對低頻的位置。
因此,使用傳統平均模型指導環路設計時,穿越頻率一般被限制在開關頻率的約1/10~1/5處。 另一方面,實際的開關變換器系統環路很多是類二階系統,這個位置的帶寬設計也是幫助實現充足相位裕量的權衡之舉。
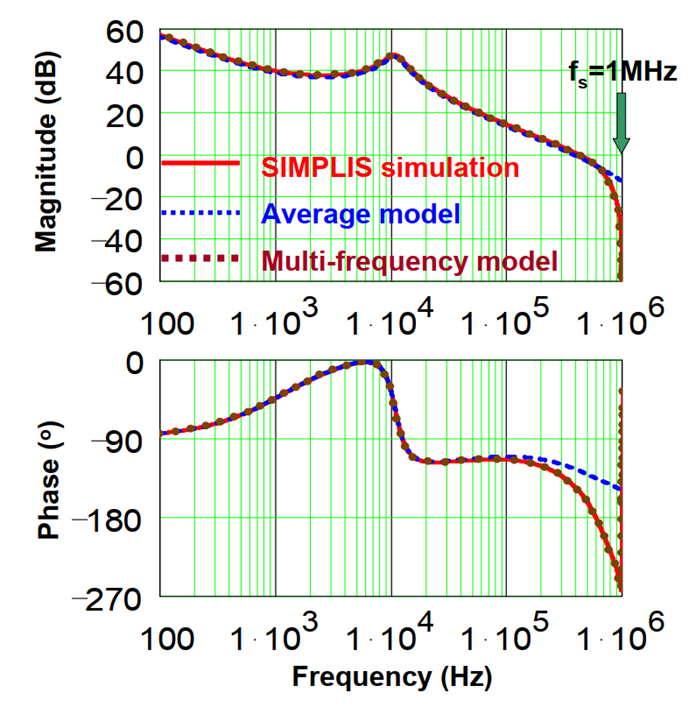
若找到適用于時變系統的建模方法,最后的小信號模型便可解除低頻有效的限制,如上圖中的“多頻率模型”。
同樣的,如果能找到突破“低頻”,“小紋波”,“小信號”三個假設的其他建模方法,自然可以提高建模的精確度。 下一節將將要介紹這些多樣的建模方法。
解析法建模的分類和舉例
除了適用于計算機仿真的數值計算建模手法,回答問題4,從理論角度通過解析法建模主要有以下手段。
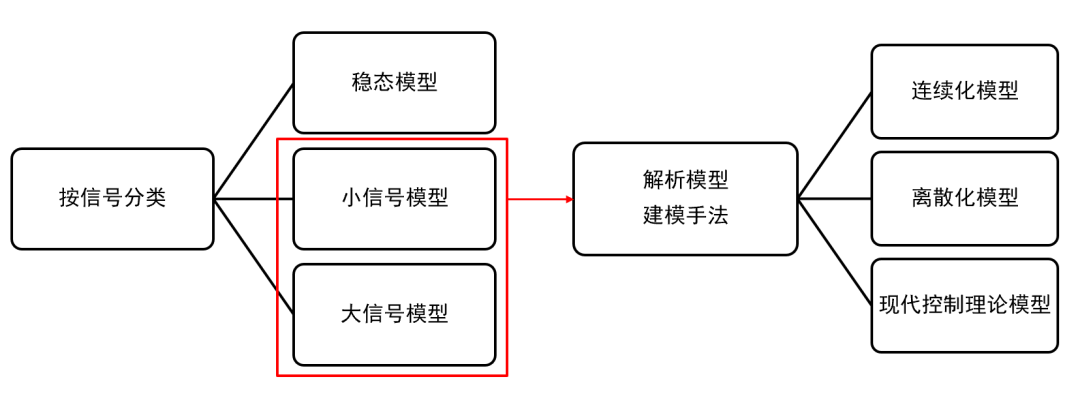
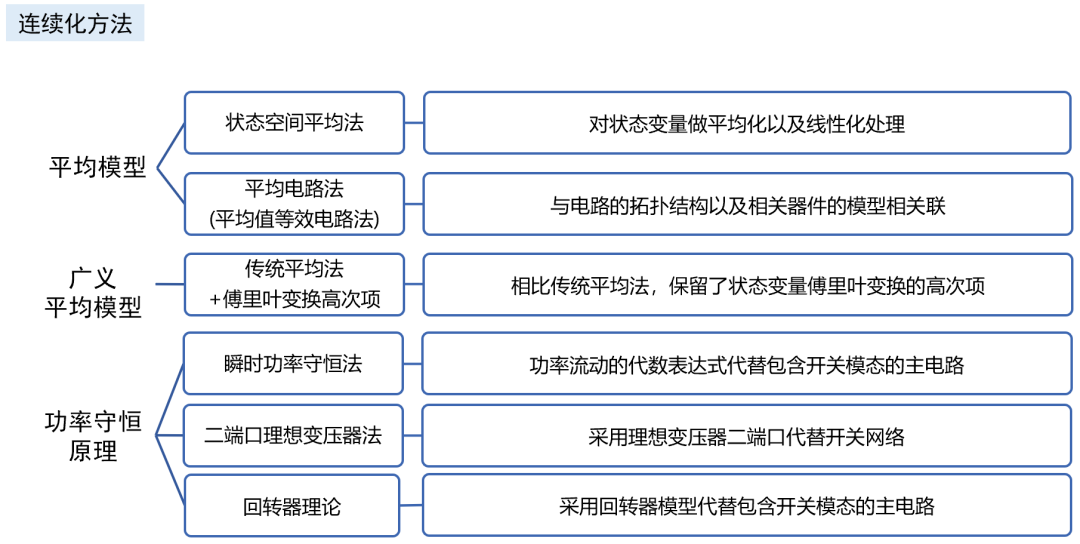
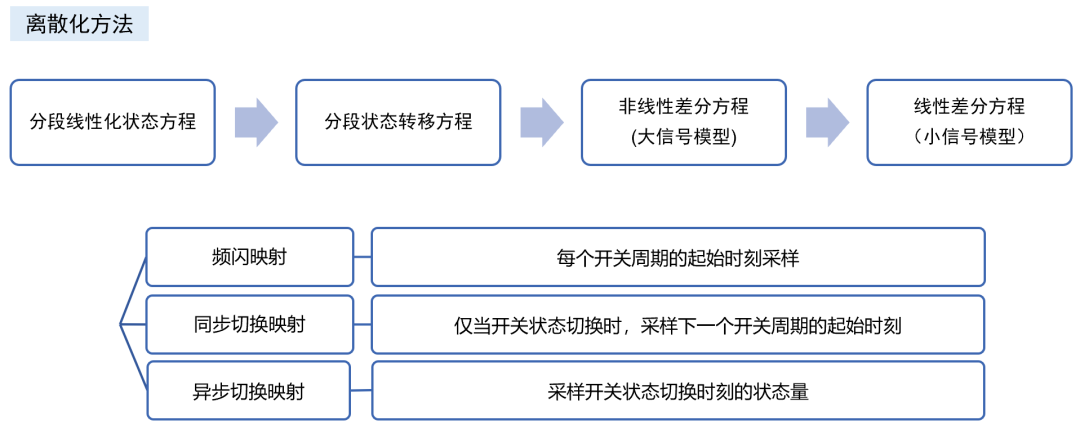
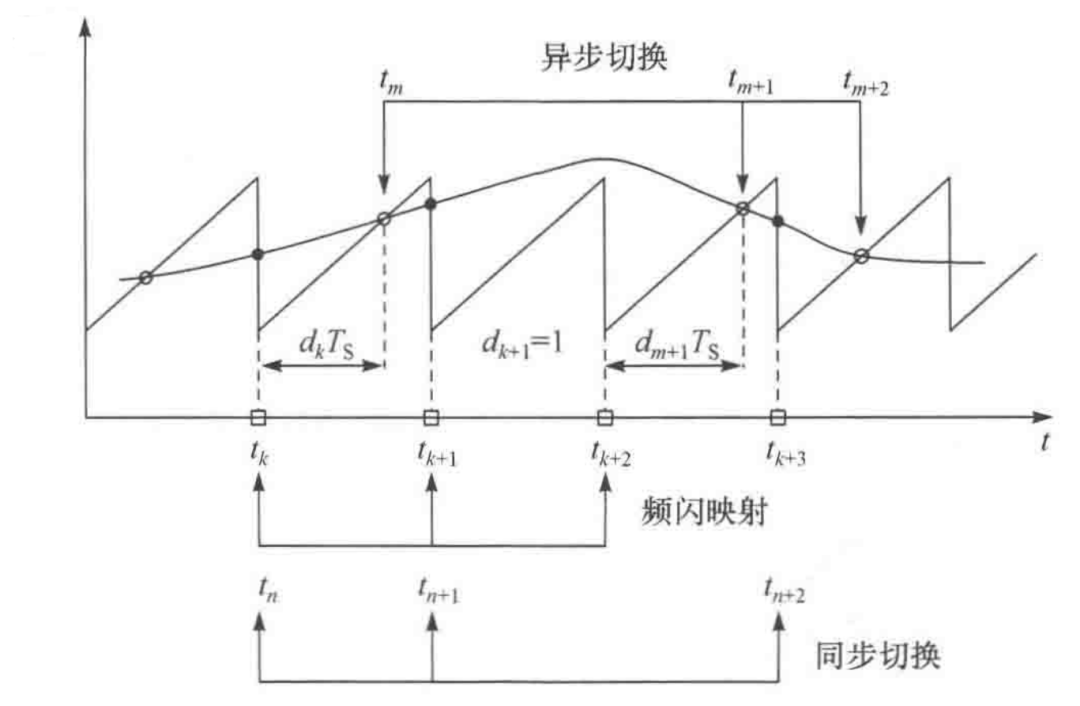
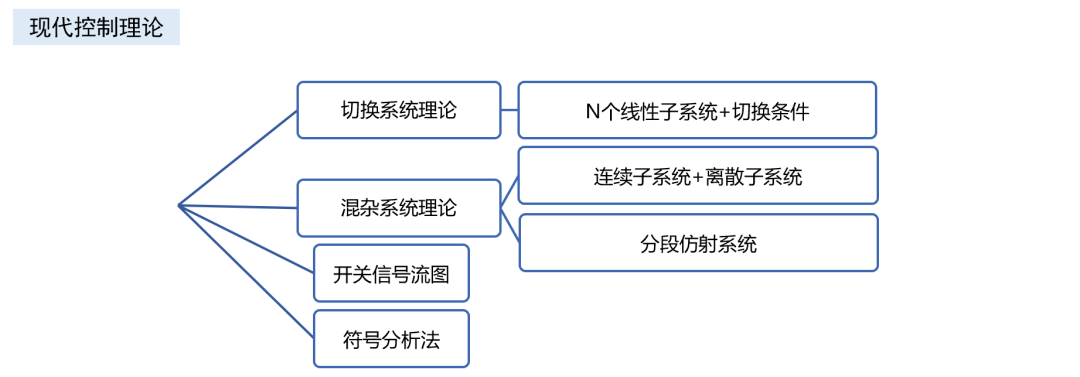
除了最經典的開關平均模型,最常見的應當是離散采樣迭代模型 ,離散模型遵循了PWM調制器作為采樣保持器的本質,不必拘泥于滿足平均模型的“低頻”“小紋波”“小信號”等所有假設,能 求解精準的大信號非線性動力學行為模型 ,并還原出1/2*fsw頻率處的小信號模型。 它和平均模型的轉換關系如下。
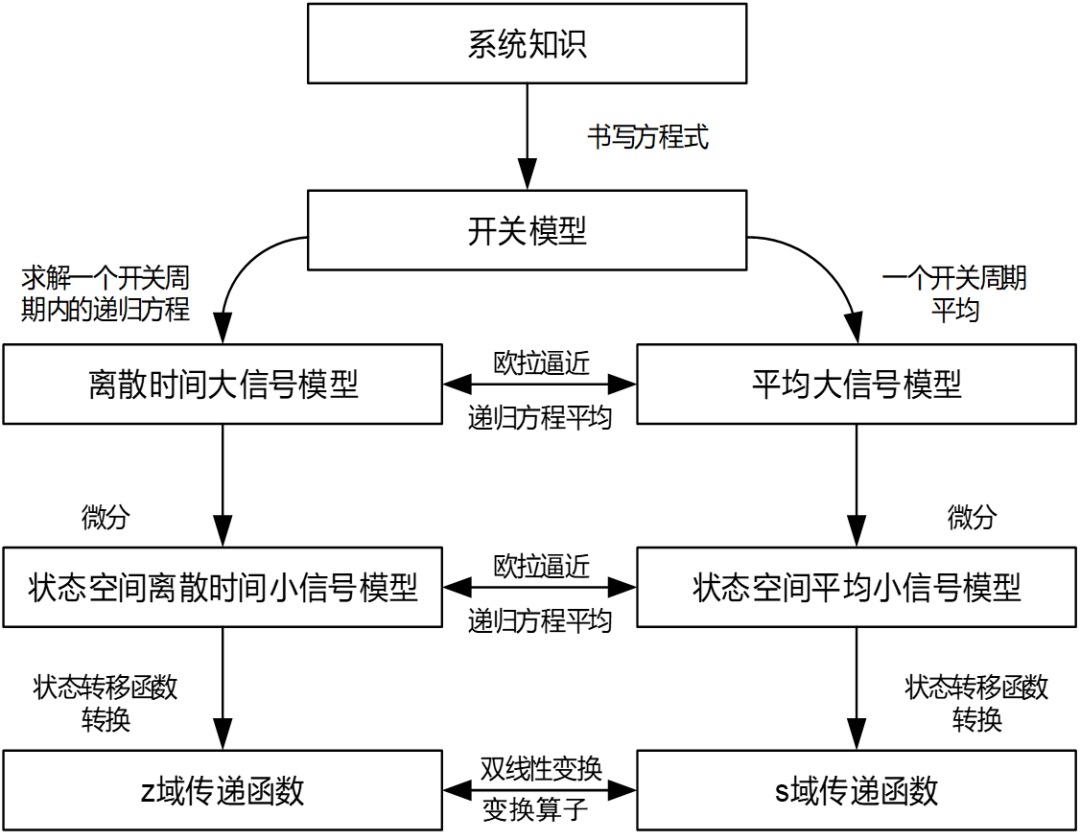
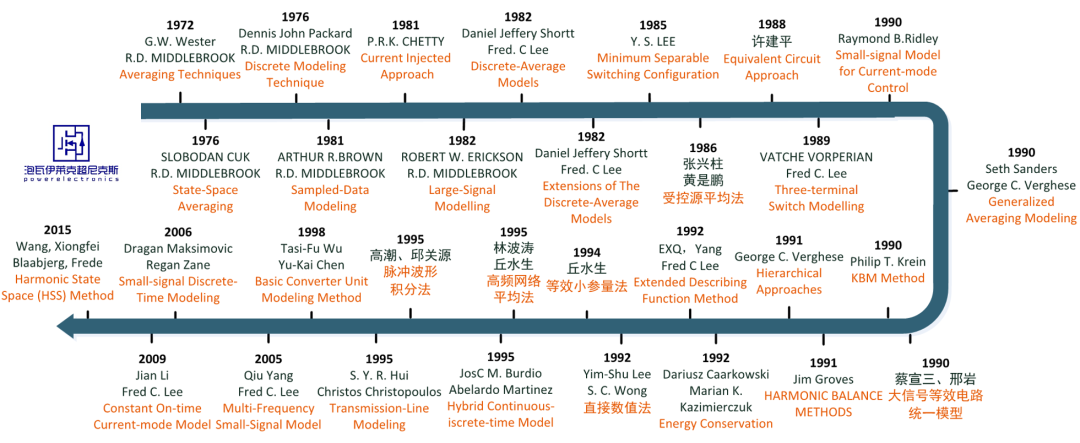
建模方法的發展歷史
選取部分被引量較高的、有代表性的建模方法,按時間線羅列如下。
選取具有較強主觀性,僅供參考,如有遺漏還請包涵
大信號穩定性和小信號穩定性
既然我們可以借助離散模型,建立精準的動力學行為模型,利用非線性系統的分析手段,勢必可以發現開關變換器更多的動態運行規律。
和線性系統的穩定性定義不同,非線性系統存在多個平衡態(包含平衡點或周期平衡態),其 穩定性一般指平衡態的局部穩定性 (可進一步明確局部的范圍有多大),可用如下方法判斷:
- 平衡點:李雅普諾夫Lyapunov穩定性
- 周期平衡態:龐加萊Poincare穩定性
回答 問題5 , DC-DC開關變換器,其非線性的大信號模型,平衡點的局部穩定性,類似于穩態工作點,線性化后小信號模型的穩定性,區別在于 非線性的大信號可以借助李雅普諾夫函數的構造進一步明確局部的范圍大小,而不僅僅是小信號模型中模糊的"附近"。
非線性系統的大信號 失去平衡態后,其動力學行為可用分岔與混沌理論進行解釋和預測 ,典型的分岔行為有:
- 霍普夫hoph分岔,不期望的周期平衡態,也就是“極限環”低頻振蕩
- 倍周期分岔,也就是次諧波振蕩
如下給出了發生低頻振蕩,和次諧波振蕩的波形實例。
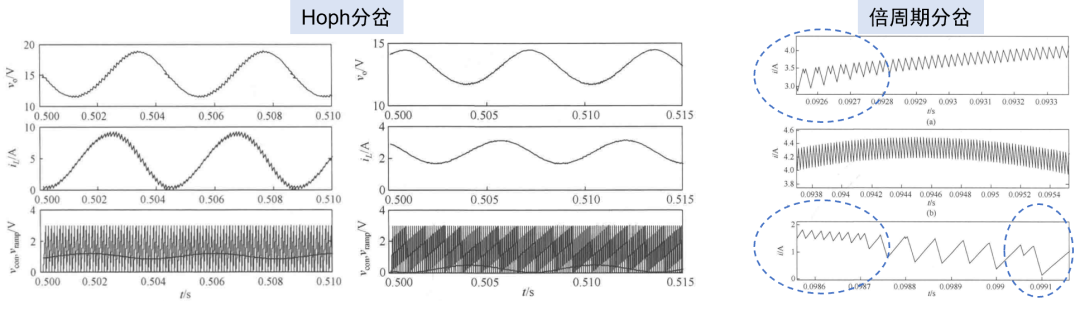
在失穩之前直到臨界穩定狀態,小信號模型依然有效,可以預測臨界穩定的條件。
在失穩之后,意味著不能穩定在該穩態工作點,小信號模型失效,在大信號上可能表現為低頻振蕩(霍普夫hoph分岔)或次諧波振蕩(倍周期分岔),以及其他更復雜的動力學行為。
通過對小信號模型臨界穩定的具體特征進行識別,可以在一定程度上預測失穩以后的行為。 但其充要條件必須嚴格來自于分岔與混沌理論的推導,極少文獻對此進行嚴格證明。
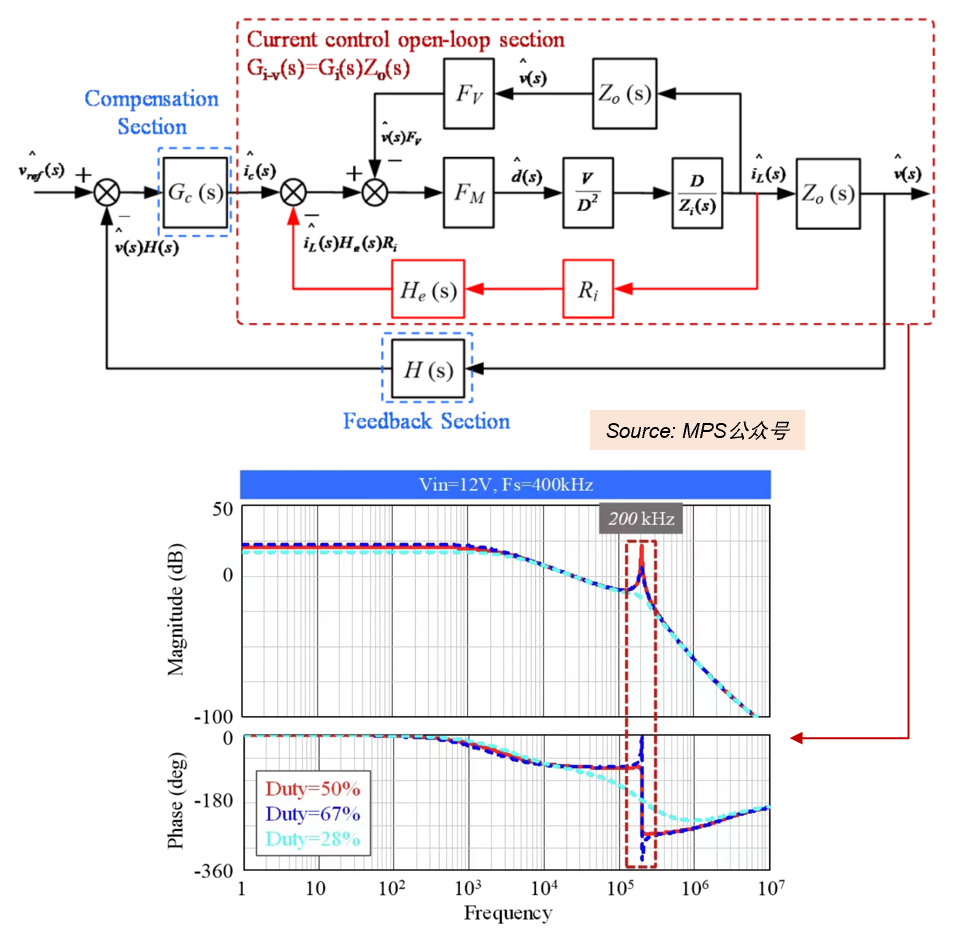
- 如下為小信號波特圖,預測Buck電壓模式控制中,低頻振蕩(霍普夫hoph分岔)臨界條件(Kp足夠大)的實例。
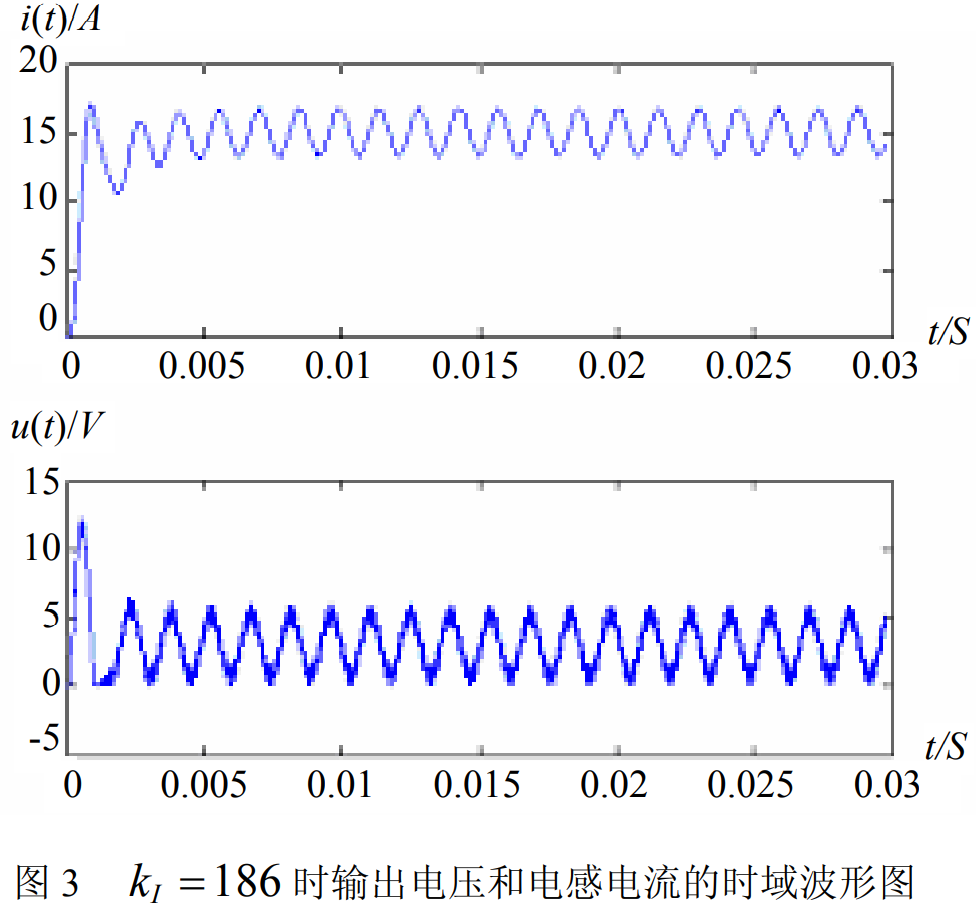
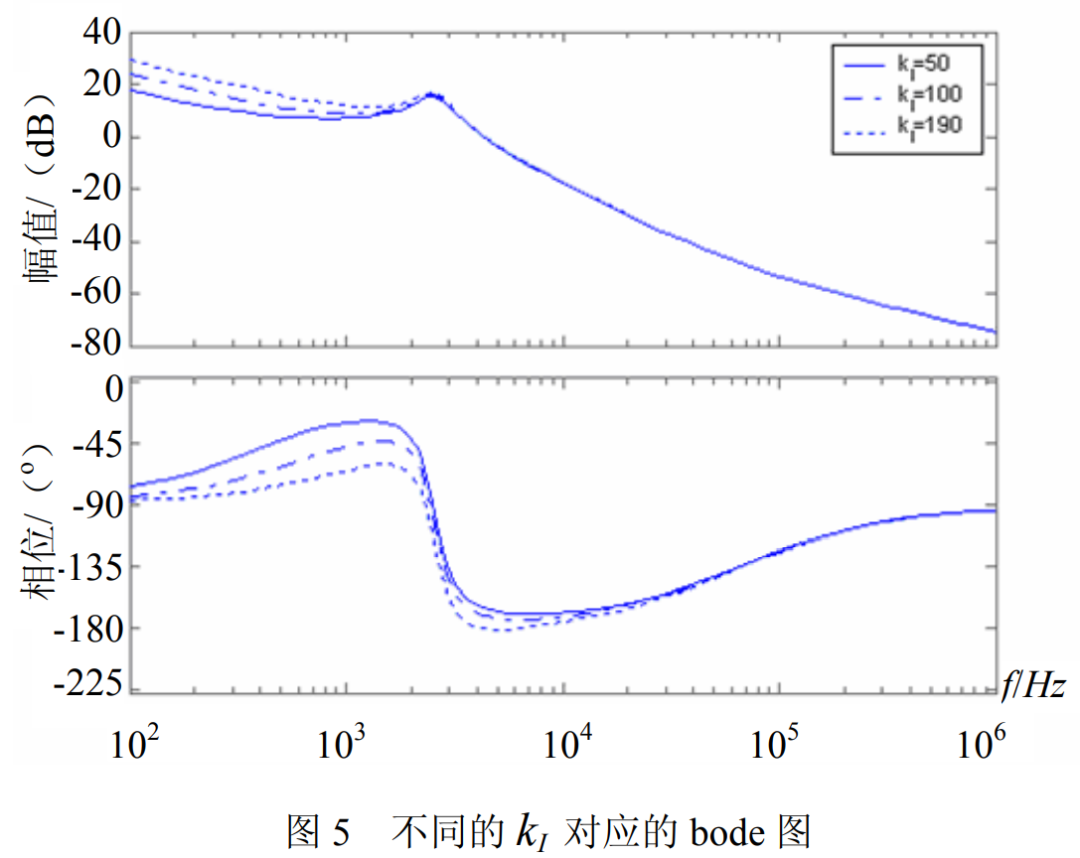
- 如下為小信號波特圖,預測Buck峰值電流控制中,次諧波振蕩(倍周期分岔)臨界條件(D=0.5)的實例。
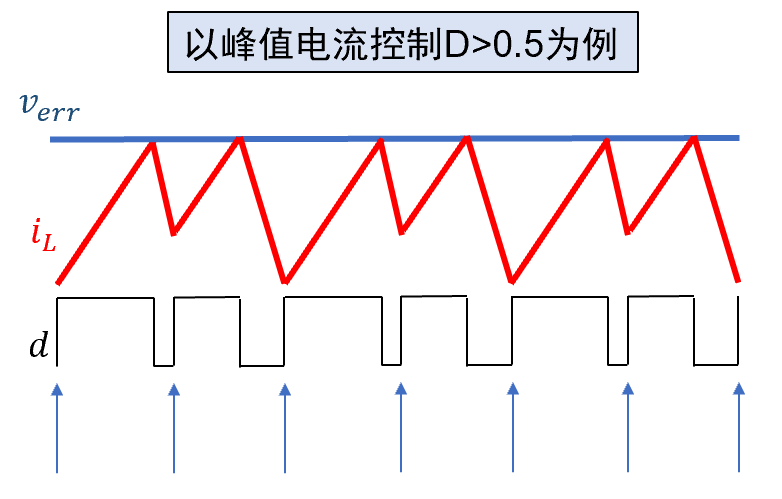
-
BUCK
+關注
關注
32文章
483瀏覽量
64283 -
PWM
+關注
關注
114文章
5196瀏覽量
214461 -
變換器
+關注
關注
17文章
2107瀏覽量
109434 -
小信號
+關注
關注
1文章
52瀏覽量
12201 -
大信號
+關注
關注
0文章
9瀏覽量
7526
發布評論請先 登錄
相關推薦
單級BUCK-BOOST變換器實現APFC的原理及分析
buck級聯推挽變換器小信號建模的問題
BUCK變換器設計
Buck變換器參數辨識的分析
DCM_Buck_Boost變換器的建模與控制設計講解
buck變換器設計_自制buck變換器
buck變換器的濾波電容電感怎么選取及用法

理想buck變換器模型與非理想buck變換器模型
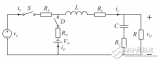
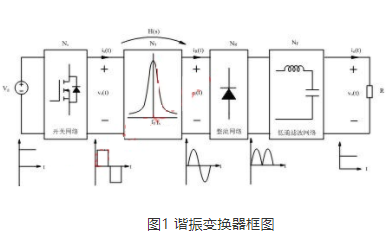
諧振變換器到底是什么及理想和非理想buck變換器的模型介紹
Buck變換器的工作原理與設計的學習課件免費下載
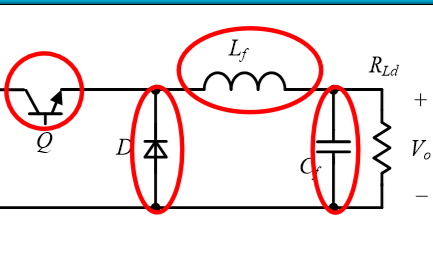




 基于Buck變換器的大小信號模型
基于Buck變換器的大小信號模型










評論